1)Множества. Включения и равенство множеств. Свойства.
Множество есть совокупность различных элементов, мыслимая как единое целое.
В математической логике и дискретной математике часто употребляемый синоним множества — алфавит. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.
Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А).
Два
множества
и
могут
вступать друг с другом в различные
отношения.
включено в , если каждый элемент множества принадлежит также и множеству :
включает , если включено в :
равно , если и включены друг в друга:
строго включено в , если включено в , но не равно ему:
строго включает , если строго включено в :
и не пересекаются, если у них нет общих элементов:
и
не
пересекаются
и находятся в общем положении, если существует элемент, принадлежащий исключительно множеству , элемент, принадлежащий исключительно множеству , а также элемент, принадлежащий обоим множествам:
и
находятся
в общем положении
Смешанные свойства
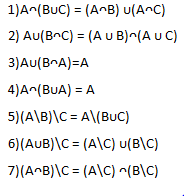
2) Операция объединения и пересечения множест. Свойства.
Свойства объединения множеств
Свойства
пересечения множеств
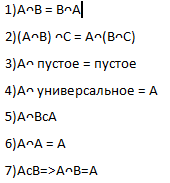
3)Разность и симметричная разность. Свойства.
Свойства разности множеств
Свойства
усечённой разности множеств
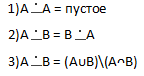
4) Пустое и универсальное множество
Пусто́е мно́жество (в математике) — множество, не содержащее ни одного элемента.
Свойства пустого множества
Ни одно множество не является элементом пустого множества. Иначе говоря,
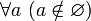и,
в частности,
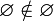.Пустое множество является подмножеством любого множества. Иначе говоря,
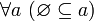и,
в частности,
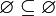.Объединение пустого множества с любым множеством равно последнему [указанному множеству]. Иначе говоря,
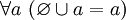и, в частности,
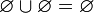.Пересечение пустого множества с любым множеством равно пустому множеству. Иначе говоря,
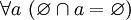и,
в частности,
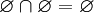.Исключение пустого множества из любого множества равно последнему [указанному множеству]. Иначе говоря,
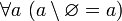и,
в частности,
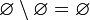.Исключение любого множества из пустого множества равно пустому множеству. Иначе говоря,
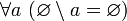и,
в частности,
.Симметрическая разность пустого множества с любым множеством равна последнему [указанному множеству]. Иначе говоря,
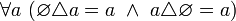и,
в частности,
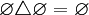
Декартово произведение пустого множества на любое множество равно пустому множеству. Иначе говоря,
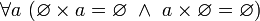и,
в частности,
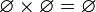.Пустое множество — транзитивно. Иначе говоря,
,
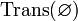где
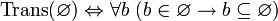.Пустое множество — ординал. Иначе говоря,
,
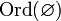где
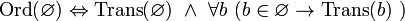.Мощность пустого множества равна нулю. Иначе говоря,
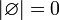.Мера пустого множества равна нулю. Иначе говоря,
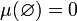
Универса́льное мно́жество — в математике множество, содержащее все мыслимые объекты. Универсальное множество единственно.
Свойства универсального множества
Любой объект, какова бы ни была его природа, является элементом универсального множества.
В частности, само универсальное множество содержит себя в качестве одного из многих элементов.
Любое множество является подмножеством универсального множества.
В частности, само универсальное множество является своим подмножеством.
Объединение универсального множества с любым множеством равно универсальному множеству.
В частности, объединение универсального множества с самим собой равно универсальному множеству.
Пересечение универсального множества с любым множеством равно последнему множеству.
В частности, пересечение универсального множества с самим собой равно универсальному множеству.
Исключение универсального множества из любого множества равно пустому множеству.
В частности, исключение универсального множества из себя равно пустому множеству.
Исключение любого множества из универсального множества равно дополнению этого множества.
Дополнение универсального множества есть пустое множество.
Симметрическая разность универсального множества с любым множеством равна дополнению последнего множества.
В частности, симметрическая разность универсального множества с самим собой равна пустому множеству.
