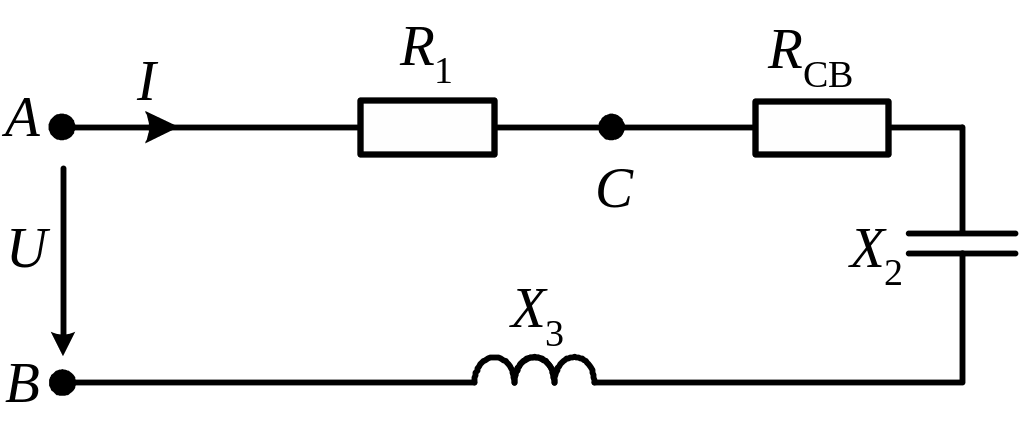
Пример расчёта задания №2

Пример расчёта приводится для варианта 2.БВ.20 (дан с другими числовыми данными).

Дано: ; ; ; ; ; .

Определить показания приборов , используя метод эквивалентных преобразований.

Порядок расчёта

1. Вычислим реактивные сопротивления ветвей: ;

2. Определим полное сопротивление второй ветви из треугольника сопротивлений: .

3. Преобразуем участок CB в эквивалентный, содержащий только параллельные ветви и тогда схема участка CB примет вид:

Рис. 2.2.

4. Вычислим значения активных и реактивных проводимостей участка CB: ; ;

5. Значения эквивалентных проводимостей участка CB: ; ;

6. Определим величины эквивалентных сопротивлений участка CB: ;

X_CB – индуктивное сопротивление, т.к. и b_CB – индуктивная проводимость.

7. Заменим участок CB, содержащий параллельное соединение элементов, и тогда получим схему, содержащую только последовательное соединение элементов:

Рис.2.3.

8. Вычислим полное сопротивление цепи: .

9. Определим показания амперметра A₁, то есть ток в неразветвленной части цепи по закону Ома:

10. Определим угол фазового сдвига между током в неразветвленной части цепи и напряжением, приложенным к зажимам цепи:

11. Вычислим показание ваттметра W₁:

12. Вычислим показание вольтметра V₂, т.е. напряжение на участке CB:

13. Определим ток во второй ветви по закону Ома:

14. Угол фазового сдвига для этой ветви определим из треугольника сопротивлений:

15. Определим ток в третьей ветви:

16. Угол сдвига для этой ветви:

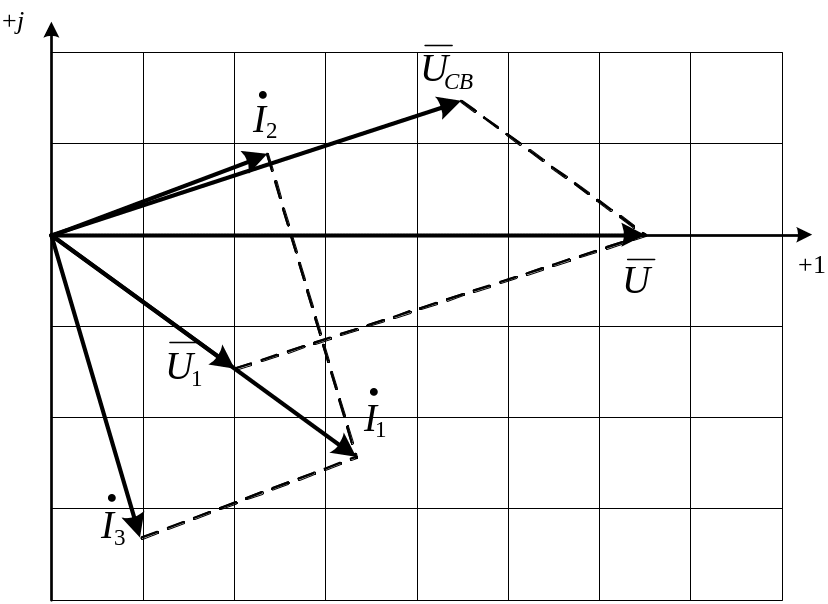
17. Векторную диаграмму токов и напряжений строим в следующей последовательности (рис. 2.4):

а) выбираем масштабы для напряжения и тока: ;

б) строим вектор напряжения, приложенного к зажимам цепи ;

в) затем строим вектор тока в неразветвленной части цепи , который сдвинут относительно вектора на угол ;

г) строим вектор напряжения на сопротивлении в неразветвленной части цепи, который равен

Этот вектор совпадает по фазе с вектором тока .

д) вектор напряжения на участке CB строим на основании второго закона Кирхгофа:

е) угол фазового сдвига для вектора напряжения относительно вектора тока :

или

ж) строим вектор тока , который сдвинут относительно напряжения на угол ;

з) вектор тока строим под углом относительно напряжения

Рис.2.4.

Пояснения к выбору исходных данных и метода расчета для задачи №3.

Исходные данные определяются номером варианта, который задается набором из шести цифр (01.111.1-25.999.6).

Первые две цифры, отделенные точкой указывают номер схемы (рис. 3); Третья цифра показывает величину сопротивления R (Ом) и величину заданного тока I (А) или напряжения U (В); Четвертая цифра показывает величину индуктивности L (мГн) ; Пятая цифра, увеличенная в 100 раз показывает величину емкости С (мкФ); шестая цифра, отделенная точкой, указывает, какой ток или какое напряжение заданы: если цифра 1, 2 или 3 – то заданы соответственно ток , если стоит цифра 4, 5 или 6 – то соответственно задано напряжение (начальную фазу, заданной электрической величины принять равной нулю).

Например, вариант 10.562.5: схема №10, , , , .