Угол между прямыми. Угол между прямой и плоскостью.

 

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

   и      косинус угла между ними можно найти по формуле:

                  .                                                   (8.14)

Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:

   -  условие параллельности прямых,                                     (8.15)

  -   условие перпендикулярности прямых.                (8.16)

   Угол φ между прямой, заданной каноническими уравнениями

                                                                                                                                                           и плоскостью, определяемой общим уравнением 

                            Ax + By + Cz + D = 0,                                                                                                                                                                                                          можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда

                                                        (8.17)   

Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:

                     Al + Bm + Cn = 0,                                                                                (8.18)

а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов:   A/l = B/m = C/n.            

Лекция 9.

Линейные преобразования координат. Собственные векторы и собственные числа матрицы, их свойства. Характеристический многочлен матрицы, его свойства.

 

   Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору х R по некоторому правилу поставлен в соответствие вектор Ах R.

 

Определение 9.1. Преобразование А называется линейным, если для любых векторов х и у и для любого действительного числа λ выполняются равенства:

               А(х + у)=Ах + Ау,   А(λх) = λ Ах.                                                           (9.1)

 

Определение 9.2.  Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.  

Тождественное преобразование обозначается Е:  Ех = х.

   Рассмотрим трехмерное пространство с базисом е₁, е₂, е₃, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы Ае₁, Ае₂, Ае₃, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:

                    Ае₁ = а₁₁ е₁ + а₂₁ е₂ +а₃₁ е₃,

                    Ае₂ = а₁₂ е₁ + а₂₂ е₂ + а₃₂ е₃,                                                                     (9.2)

                    Ае₃ = а₁₃е₁ + а₂₃ е₂ + а₃₃ е₃    .

Матрица 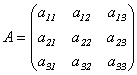     называется матрицей линейного преобразования А в базисе е₁, е₂, е_3 . Столбцы этой матрицы составлены из коэффициентов в формулах (9.2) преобразования базиса.

 

Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е.

 

  Для произвольного вектора х =х₁е₁ + х₂е₂ + х₃е₃ результатом применения к нему линейного преобразования А будет вектор Ах, который можно разложить по векторам того же базиса: Ах =х`<sub>1</sub>е<sub>1</sub> + х`₂е₂ + х`<sub>3</sub>е<sub>3</sub>, где координаты x`_i можно найти по формулам:

        х`₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃,

        x`₂ = a₂₁x₁ + a₂₂x₂ + a₂₃x₃,                                                                                     (9.3)

        x`₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃.

Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.

 

                         Преобразование матрицы линейного преобразования

                                             при переходе к новому базису.

 

   Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е₁, е₂, е₃ и е₁, е₂, е_3.  Пусть матрица С задает формулы перехода от базиса {e_k} к базису {e_k}. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно:

                                        А = С^-1АС                                                                (9.4)

Действительно,   , тогда А . С другой стороны, результаты применения одного и того же линейного преобразования А в базисе {e_k}, т.е.  , и в базисе {e_k}: соответственно   - связаны матрицей С:  , откуда следует, что СА=АС. Умножая обе части этого равенства слева на С^-1, получим  С^-1СА  = = С^-1АС, что доказывает справедливость формулы (9.4).