21.Системы эконометрических уравнений.

У₁=а₁₁х₁+а₁₂х₂+….+a_1nx_n+E₁

У₂=а₂₁х₁+а₂₂х₂+….+a_2nx_n+E₂

_{-------------------------------------------------------}

У_n=а_n1х₁+а_n2х₂+….+a_nx_n+E_n

Основным методом решения систем экономич. Уравнений является метод наименьших квадратов.(МНК)

Более сложным случаем системы экономических уравнений является случай, когда каждая предыдущая зависимая переменная «у»становится фактором «х» в другом уравнении

Сложные экономические процессы описывают с помощью системы взаимосвязанных уравнений. Различают несколько видов систем уравнений:

1. Система независимых уравнений - когда каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:

y₁=a₁₁*x₁+a₁₂*x₂+…+a_1m*x_m+e₁ Для решения этой системы и нахождения ее параметров

y_n=a_n1*x₁+a_n2*x₂+…+a_nm*x_m+e_n используется МНК.

2.Система рекурсивных уравнений – когда зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении:

y ₁=a₁₁*x₁+a₁₂*x₂+…+a_1m*x_m+e₁

y₂=b₂₁*y₁+a₂₁*x₁+a₂₂*x₂+…+a_2m*x_m+e₂

y₃=b₃₁*y₁+b₃₂*y₂+a₃₁*x₁+a₃₂*x₂+…+a_3m*x_m+e₃

y_n=b_n1*y₁+b_n2*y₂+…+b_nn-1*y_n-1+a_n1*x₁+a_n2*x₂+…+a_nm*x_m+e_n

Для решения этой системы и нахождения ее параметров используется МНК.

3 Система взаимосвязанных уравнений – когда одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую.

y ₁₌b₁₂*y₂+b₁₃*y₃+…+b_1n*y_n+a₁₁*x₁+a₁₂*x₂+…+a_1m*x_m+e₁

y₂=b₂₁*y₁+b₂₃*y₃+…+b_2n*y_n+a₂₁*x₁+a₂₂*x₂+…+a_2m*x_m+e₂

y_n=b_n1*y₁+b_n2*y₂+…+b_nn-1*y_n-1+a_n1*x₁+a_n2*x₂+…+a_nm*x_m+e_n

22.Косвенный метод наименьших квадратов.

В системе одновременных уравнений каждое уравнение не может рассматриваться как самостоятельная часть системы, поэтому оценки неизвестных коэффициентов данных уравнений нельзя определить с помощью классического метода наименьших квадратов, т. к. нарушаются три основных условия применения этого метода:

а) между переменными системы уравнений существует одновременная зависимость, т. е. в первом уравнении системы y₁ является функцией от y₂, а во втором уравнении уже y₂ является функцией от y₁;

б) наличие проблема мультиколлинеарности, т.е. во втором уравнении системы y₂ зависит от x₁, а в других уравнениях обе переменные являются факторными;

в) случайные ошибки уравнения коррелируют с результативными переменными.

Следовательно, если неизвестные коэффициенты системы одновременных уравнений оценивать с помощью классического метода наименьших квадратов, то в результате мы получим смещённые и несостоятельные оценки.

Косвенный метод наименьших квадратов используется для получения оценок неизвестных коэффициентов системы одновременных уравнений, удовлетворяющих свойствам эффективности, несмещённости и состоятельности.

Косвенный метод наименьших квадратов применяется только в том случае, если структурная форма системы одновременных уравнений является точно идентифицированной.

Алгоритм метода наименьших квадратов реализуется в три этапа:

на основе структурной формы системы одновременных уравнений составляется её приведённая форма, все параметры которой выражены через структурные коэффициенты;

приведённые коэффициенты каждого уравнения оцениваются обычным методом наименьших квадратов;

на основе оценок приведённых коэффициентов системы одновременных уравнений определяются оценки структурных коэффициентов через приведённые уравнения.

Рассмотрим применение косвенного метода наименьших квадратов на примере структурной формы модели спроса и предложения:

Было доказано, что структурная форма модели спроса и предложения является точно идентифицированной, поэтому для определения оценок неизвестных параметров данной модели можно применить косвенный метод наименьших квадратов.

1) запишем приведённую форму модели спроса и предложения:

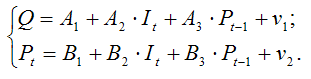
2) определим оценки коэффициентов приведённой формы модели спроса и предложения с помощью обычного метода наименьших квадратов. Тогда система нормальных уравнений для определения коэффициентов первого уравнения приведённой формы модели будет иметь вид:

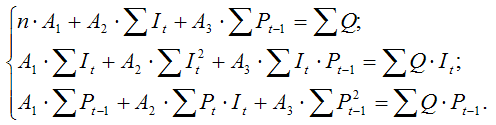
Система нормальных уравнений для определения коэффициентов второго уравнения приведённой формы модели записывается аналогично. Решением данных систем нормальных уравнений будут численные оценки приведённых коэффициентов A₁,A₂,A₃ и B₁,B₂,B₃;

Для определения по оценкам приведённых коэффициентов получить оценки структурных коэффициентов первого уравнения, необходимо из второго приведённого уравнения выразить переменную I_t и подставить полученное выражение в первое уравнение приведённой формы модели. Для определения оценок структурных коэффициентов второго уравнения, необходимо из второго приведённого уравнения выразить переменную P_t–1 и подставить полученное выражение в первое уравнение приведённой формы модели.