8. Проекция векторов на ось.

Проекция вектора на ось называется длина отрезка оси, начало которой является проекцией начала вектора и конец – проекция конца вектора.

Знак вектора будет положительным, если направление вектора совпадает с направление оси и наоборот.

Теоремы о проекции векторов:

1. Проекции векторов на параллельные и одинаковые направления оси равны.

2. Проекция на ось равна по модулю проецируемого вектора умноженного на косинус угла положительного вектора оси.

3. Проекции геометрической суммы нескольких векторов, равно алгебраической сумме нескольких векторов.

9. Уравнение равновесия сходящихся сил.

Равнодействующая:

R = F₁ + F₂ + ... + F_n = SF_k Возьмем прямоугольную систему координат XY и спроецируем каждую из частей уравнения на оси X и Y. Fx и Fy – проекции. X и y - равнодействующая составляющей.

Fx=x1+x2+…x_n

Fy=y1+y2+y_n

Вектор F:

В случае равновесия F=0. X=0 и y=0.

Для равновесия системы сходящихся сил необходимо. Чтобы проекции всех сил на каждую из координат осей равнялись 0!

10. Разложение сил на составляющие.

Задача   отыскания   нескольких сил, равнодействующей которых была бы данная сила. Эта задача может приводить к различным решениям, подобно тому как это имеет место при разложении вектора перемещения.

Чтобы задача о разложении силы стала определенной (т. е. имела бы только одно решение), необходимы дополнительные указания. Например, если заданы величина и направление одной из составляющих или два направления, по которым должны действовать составляющие, и т. п., то операция разложения силы на две составляющие становится вполне определенной и сводится к простому геометрическому построению.

Пусть, например, мы хотим разложить силу F  на две составляющие, лежащие в одной плоскости с F¹ и направленные вдоль прямых АВ и АС (рис. 104). Для этого достаточно из конца вектора, изображающего F, провести две прямые, параллельные АВ и АС. Отрезки F₁ и F₂ изобразят искомые силы.

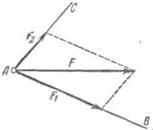
Рис. 104. Разложение данной силы F по заданным направлениям АВ и АС.

Обычно в стоящих перед нами механических задачах содержатся указания на то, как целесообразнее разложить силу на составляющие. Часто условия задачи прямо указывают те направления, по которым нужно найти составляющие данной силы. Например, чтобы отыскать силы натяжения тросов, на которых висит груз, нужно силу тяжести Р груза разложить на составляющие Р₁ и Р₂ по направлениям этих тросов (рис. 105). Натяжения тросов должны уравновесить эти составляющие. Как легко видеть, чем больше угол между тросами, тем больше окажутся силы натяжения тросов. Поэтому если расстояние между опорами тросов велико, то даже небольшой груз, если он висит немного ниже опор, вызывает очень большое натяжение тросов. Этим объясняется, почему гололед или иней иногда обрывает туго натянутые провода.

При разложении силы на три или большее число составляющих увеличивается и число условий, необходимых для того, чтобы разложение было выполнено однозначно.

Рис. 105

Чем больше угол ВАС между тросами, тем больше силы натяжения тросов.