48. Работа равнодействующей силы, приложенной к одной точке.

На движущуюся точку М действуют силы Р₁,Р₂, … Р_n, равнодействующая которых

Р = Р₁ + Р₂ + … + Р_n (1)

Обе части этого равенства спроецируем на направление скорости υ:

P cosα = Р₁cosα₁ + P₂cosα₂ + … + Р_ncos α_n (2)

где α,α₁, α₂, … α_n — углы между соответствующими силами и скоростью.

Умножив обе части равенства на ∆s, получим

P ∆scos α = Р₁ ∆scosα₁ +P₂ ∆scos α₂ + … + Р_n ∆scosα_n (3)

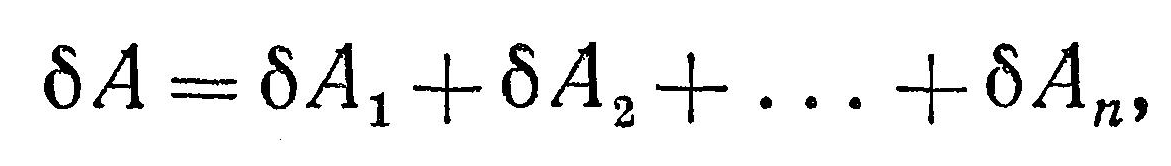т. е. элементарная работа равнодействующей силы на бесконечно малом перемещении ∆s равна сумме элементарных работ составляющих сил на том же перемещении.

Предположим, что конечное перемещение M₁M₂ движущейся точки разбито на бесконечно малые перемещения. Для каждого из них можно написать равенство, аналогичное (4). Складывая эти равенства почленно и переходя к пределу, получаем:

Или

Вывод: Мы доказали, что работа равнодействующей силы равна алгебраической сумме работ составляющих сил

49. Работа сил тяжести.

Пусть точка М приложения силы тяжести G перемещается из М₁ в М₂ по некоторой кривой.

Разобьем дугу М₁М₂ кривой произвольно на n частей.

Рассмотрим некоторую часть длиной ∆s.Элементарная работа силы тяжести на перемещении ∆s.

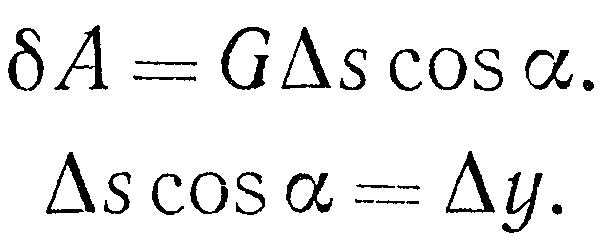
Работа силы тяжести при опускании точки М из М₁ в М₂

Предел вычисляется при условии, что n—> ∞, а ∆у—>0. Полученный предел представляет собой определенный интеграл:

Постоянный множитель G может быть вынесен за символ определенного интеграла.

Определенный интеграл равен разности значений первообразной функции от подынтегральной функции при верхнем и нижнем пределах интегрирования:

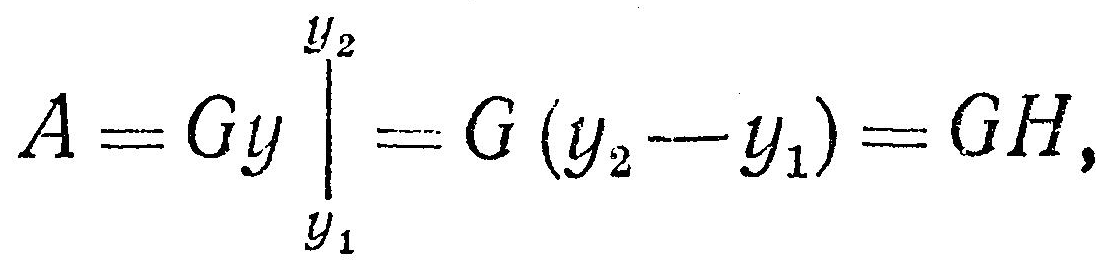
Если изменить направление точки, то мы получим:

Работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения.

50. Работа сил упругой пружины.

К грузу М в некоторый момент движения приложены сила тяжести G и реакция пружины R. Эта реакция называется упругой силой пружины. Еe модуль принимают пропорциональным удлинению ОМ:

где с—коэффициент пропорциональности, называемый коэффициентом жесткости.

Приняв за ось Ох—ось, проходящую через ОМ вниз и за начало координат точку О, можем записать:

Наша реакции является переменной величиной и функции перемещения. Необходимо вычислить работу силы тяжести при перемещении груза из т. О в M₁

Работа силы R на перемещении h:

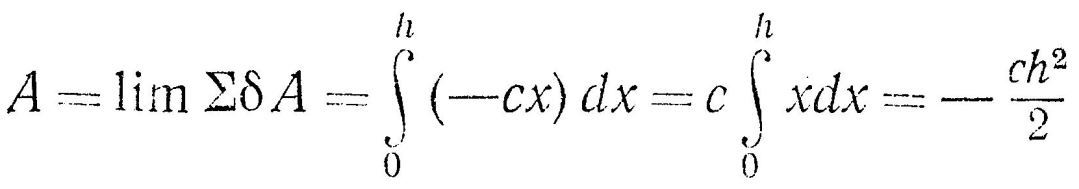
При движении точки М вверх из положения М₁ в положениеО

51. Мощность.

Мощность характеризует быстроту изменения работы в данный момент.

Средней мощностью Nср за некоторый промежуток времени называется отношение работы силы на соответствующем перемещении точки ее приложения к этому промежутку времени.Средняя мощность за промежуток времени ∆t . Мощностью N в данный момент называется предел средней мощности при ∆t —> 0.

В системе СИ единицей мощности является ватт.

Мощность N может быть выражена через υ скорость:

В частном случае, когда Р и υ совпадают, N = Рυ

53. КПД.

Силы, приложенные к звеньям машины, подразделяют на задаваемые и реакции связей. Задаваемые силы не входят в число реакций. К ним относятся движущие силы, силы полезных сопротивлений и силы тяжести звеньев машины. Силы полезных сопротивлений приложены к исполнительным звеньям машины. Назначение машины — преодоление этих сил.

Обозначим абсолютные величины работ движущих сил, полезных и вредных сопротивлений соответственно А_дв, А_{пол.сопр},иА_вр.соп.

Рассмотрим установившееся движение машины, т. е. такое при котором соблюдается равенство:

Механический коэффициент полезного действия (к.п.д.):

Коэффициент полезного действия η = 0, когда А_{пол.сопр}=0, т.е. при холостом ходе.