45. Метод кинетостатики для материальной точки.

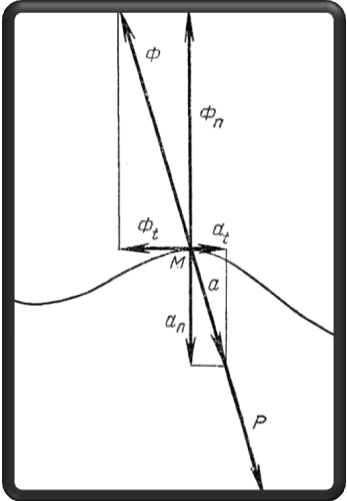
Несвободная точка М движется по траектории под действием сил. Равнодействующая сила Р равна геометрической сумме активной силы Ракт и реакции связи R.

Перепишем основное уравнение динамики: mа=Ракт+R(1) в виде Ракт+R-ma=0.

mа —вектор, модуль которого имеет одинаковую размерность с силой. Этот вектор можно рассматривать как некоторую силу, не приложенную к точке М. Обозначим его Ф = - mа (3)

Эта сила получила название - сила инерции материальной точки. Силой инерции материальной точки называется вектор по модулю, равный произведению массы точки на модуль ускорения, направленный противоположно ускорению.

Р_акт+R=Ф=0 (4)

Уравнение (4) называется уравнением кинетостатики для несвободной, т. е. находящейся под действием связей, материальной точки.

Сила инерции приложена не к данной точке М, а к телу, действующему на точку М и сообщающему ей ускорение.

Введение вектора Ф позволяет установить новый метод решения задач.динамики—метод кинетостатики.

Решением задач динамики сводится к решению статической задачи, т.е. решению по форме, а не по существу, так как дано движение, а не равновесие.Составляющие силы Ф по касательной и нормали к траектории называются соответственно касательной (или тангенциальной) инормальной (или центробежной) силами инерции.

Их модули определяются из формул:

где р — радиус кривизны траектории.

Если движущаяся точка принадлежит вращающемуся вокруг неподвижной оси твердому телу, то:

где h—расстояние от точки до оси вращения.

46. Работа постоянной силы на прямолинейном участке цепи.

Д ана постоянная по модулю и направлению сила Р, точка М приложения которой перемещается прямолинейно из М1 в M2.

Работой А постоянной силы Р на прямолинейном перемещении называется произведение модуля силы на перемещение и на косинус угла между силой и скоростью перемещению точки

A = P s cosα (1) ,где s = М₁М₂— перемещение точки М;

а — угол между силой Р и скоростью V.

Уравнение (1) можно рассматривать в нескольких случаях:

1. Угол α острый, т.е. ˂90⁰ =>cosα>0 и А>0;

2. 180⁰<α˂90⁰ => A<0;

Частные случаи: α = 0⁰ =>A_MAX=PS;

α = 90⁰ =>A=0;

α = 180⁰ =>A_MIN= - PS;

Единицы работы.

В международной системе:

A = 1 джоуль (дж)— это работа, совершенная силой в 1 ньютон на перемещении, совпадающем с направлением силы, равном 1 метру,

1 дж= 1 н*1 м

В технической системе:

1 килограммометр (кг*м) — работа, совершенная силой в 1 килограмм на перемещении вдоль ее линии действия, равном 1 метру,

1 кГ*м =1 кГ*1 м

1. кГ*м =9,81 дж

47. Работа переменной силы на криволинейном пути.

Разобьем дугу М₁М₂ на большое число n весьма малых дуг, длины которых обозначим соответственно ∆S₁, ∆S₂… ∆S_I… ∆S_n. Приложенных к точки М со скоростью υ_I. Сила, которая будет действовать в данный момент, займет некоторую силу Р_I. Угол между скоростью υ_I и силой Р_I - α_I. Будем считать Р_I постоянной (по модулю и направлению) на перемещении, равном ∆S_I. При этом условии можно найти работу силы P_i . Ее принято называть элементарной.

Элементарной работой силы Р_I на перемещении ∆S_I- называется произведение δА_I =Р_I ∆S_I cosα_I (1)

Работой силы Р из М₁ в М₂ называется предел суммы элементарных работ при условии, что n—> ∞,а ∆S_I—> 0, то А = lim∑ Р_I ∆S_Icosα_I (2)