1.Простір товарів і відношення переваги
Нехай 
–
число наявних товарів, товари пронумеровані
від 1 до
.
Припустимо, що всі товари є довільно
подільні. Кожен споживчий набір описується
вектором 
.
Таким чином, споживчі набори ототожнюємо
з точками простору 
,
який назвемо простором
товарів.
Часто
простір товарів звужують до певної
множини 
,
найчастіше за 
приймають
невід’ємний ортант 
.
Невід’ємність елементів вектора 
означає,
що кожний товар може бути присутнім (
)
або відсутнім (
)
в споживчому наборі, але не розглядаємо
ситуації, коли споживач позбувається
певної кількості товару.
[ред.]Відношення (слабкої) переваги
Відношення
переваги (деколи кажуть відношення
слабкої переваги) –
це рефлексивне, повне та транзитивне (бінарне)
відношення 
на
просторі товарів
.
Отже,
задовільняє
аксіоми:
(A1) 
(рефлексивність)
(A2) 
(повнота)
(A3) 
виконується 
(транзитивність)
Властивість рефлексивності є формальним наслідком повноти, аксіома (A1) подана окремо для зручності.
Пара 
називається
полем переваг. 
означає,
що споживач надає перевагу набору x над
набором y або
ці набори є рівноцінні для споживача і
читається читається „x переважає y”,
„x слабо
переважає y”
або „x не
гірше за y”.
[ред.]Відношення байдужості та строгої переваги
Відношення переваги дозволяє ввести два додаткові відношення на просторі товарів:
Відношення байдужості:
.
Запис 
означає,
що ці набори є рівноцінні для споживача
і читається „x рівноцінне y”,
„x перебуває
у відношенні байдужості до y”.Відношення строгої переваги:
.
Запис 
означає,
що набір
є
для споживача кращим за набір 
і
читається „x строго
переважає y”,
„x краще
за y”.
З
аксіоми повноти та наведених означень
відношення байдужості та строгої
переваги випливає, що 
виконується
рівно одне з відношень 
або 
.
Відношення байдужості та строгої переваги мають такі властивості:
Відношення
є
іррефлексивне, тобто не існує такого 
,
що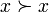 
Відношення є транзитивне, тобто
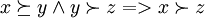
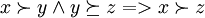
відношення байдужості є відношенням еквівалентності, тобто задовільняє властивості
рефлексивності
транзитивності
симетричності
Оскільки відношення байдужості є відношенням еквівалентності на , то воно розбиває на класи еквівалентності, які називають класами байдужості. Кожний такий клас складається з попарно байдужих наборів.
[ред.]Додаткові властивості відношення переваги
Аксіоми (А1), (А2), (А3) впроваджують відношення порядку на класах байдужості у просторі товарів . У більшості випадків порівняння споживчих наборів володіє також додатковими властивостями. Найчастіше це є властивості монотонності, неперервності та опуклості.
[ред.]Монотонне відношення переваги
Монотонність відношення переваги означає, що споживач віддає перевагу більшим наборам над меншими. Ця властивість є згідна з поведінкою споживачів у більшості ситуацій. Часом властивість строгої монотонності формулюють як аксіому ненасичуваності споживача.
Детальніше у статті Монотонне відношення переваги .
[ред.]Неперервне відношення переваги
Неперервність відношення переваги означає, що якщо споживач віддає перевагу набору над набором , то він також віддасть перевагу наборам близьким до над наборами близькими до .
З неперервності випливає, що переміщаючись від набору гіршого за довільно вибраний набір до кращого за , по дорозі завжди натрапимо на набір байдужий стосовно .
Якщо
відношення переваги є монотонним та
неперервним, то класи байдужості будуть
гіперповерхнями. У випадку двох товарів
(тобто 
)
класи байдужості називаютькривими
байдужості.
Детальніше у статті Неперервне відношення переваги .
[ред.]Опукле відношення переваги
Опуклість відношення
переваги — це властивість, що описує
схильність споживача до збалансованого
споживання наявних товарів. На приклад,
якщо споживач стверджує, що набір
складений
з двох однакових пачок кави та
набір
складений
з двох однакових пачок чаю є однаково
добрі (перебувають у відношенні
байдужості,
),
то можна очікувати, що середній
набір 
складений
з однієї пачки кави та однієї пачки чаю
виявиться принаймі не гіршим (
).
У випадку взаємодоповнюючих товарів
ця властивість є ще більш природньою.
Криві байдужості монотонного, неперервного та опуклого відношення переваги є спадними опуклими кривими.