4.1.4 Типы кривых распределения и характеристика крупности частиц
Кривые распределения признаков массы частиц могут иметь весьма разнообразный вид.
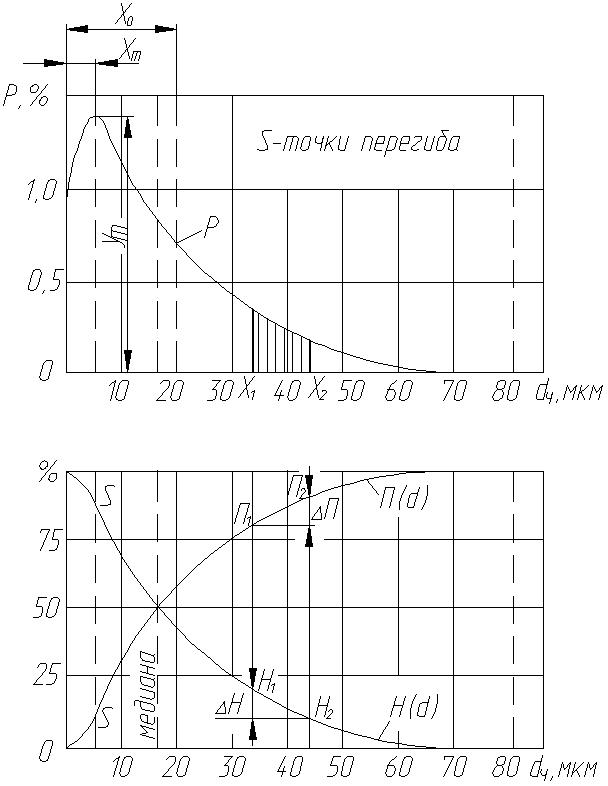
Принимая равномерным распределение частиц по размерам внутри каждой фракции, можно построить ступенчатый график, называемый гистограммой. При этом по оси абсцисс откладывают размеры частиц, а по оси ординат – относительные содержания фракций, т.е. процентное содержание каждой фракции, отнесенное к массе всего материала (рисунок 4.4, а).
Гранулометрический состав, или распределение частиц материала по размерам (диаметрам d), можно охарактеризовать, как это принято в теории вероятностей, дифференциальной кривой распределения (плотностью вероятностей) Р.
Если процентное содержание каждой фракции разделить на разность размеров частиц, принятых в качестве граничных, и найденные значения сложить в системе координат как ординаты точек, абсциссы которых равны среднему для соответствующих фракций размеру частиц, то через полученные точки можно провести плавную дифференциальную кривую распределения частиц по размерам (рисунок 4.4, б).
Однако наиболее удобным является графическое изображение результатов дисперсионных анализов в виде интегральных кривых проходов П(d) или остатков Н(d) на ситах, каждая точка которых показывает относительное содержание частиц с размерами больше или меньше данного размера (рисунок 4.4, в).
Для практических целей весьма желательно и важно охарактеризовать всю совокупность разнообразных признаков данной массы зерна или массы измельченного продукта какой-либо одной величиной, т.е. охватить кривую распределения одним числом, быть может, какой-либо одной наиболее характерной ординатой.
П
ризнаком
дифференциальной кривой распределения
могут служить абсцисса и ордината
максимума кривой распределения. Однако
этот признак не всегда достаточно
характерен, так как могут быть кривые
с минимумом (без максимума), с максимумом
и минимумом, без максимума и минимума.
а) – распределение по фракциям; б) – дифференциальная кривая распределения; в) – интегральное распределение в линейном масштабе координат
Рисунок 4.4 – Графическое изображение дисперсионного состава
Более важное значение имеет средняя ордината (или медиана), которая делит площадь, охватываемую кривой, на две части. Если через точку, соответствующую 50%, провести горизонтальную прямую до пересечения с кривыми остатков и проходов (рисунок 4.4, в), то проекция этой точки на ось абсцисс по своему значению будет медианой. При равномерном содержании фракций разной крупности в смеси кумулянта (интегральная кривая распределения) будет представлять наклонную прямую, а медиана при этом разделит весь интервал размеров сторон отверстий на две равные части; если медиана меньше середины указанного интервала, то в смеси преобладают мелкие фракции, если, наоборот, она больше, то преобладают крупные фракции.
Размеры частиц смеси могут варьировать в интервале от dо до dп, поэтому границы крупности смеси по рабочему размеру можно обозначить условным показателем К, соответствующим отношению наибольшего размера к наименьшему размеру отверстий сит:
. (4.1)
Для характеристики средней крупности смеси применяется понятие среднего диаметра. Средний размер частиц рекомендуется выражать через средневзвешенный диаметр dср, определяемый по аддитивности из соотношения:
, (4.2)
где 
,
,...,
– содержание каждой фракции в пробе
дисперсного материала, массовые доли;
,
,...,
– средний размер частиц данных фракций
(среднеарифметическое значение отверстий
сита, через которое данная фракция
прошла, и сита, на котором она задержалась).
Обычно смеси, получаемые в процессе просеивания, не соответствуют характеристике К и содержат некоторое количество частиц с размерами менее dо. Поэтому такие смеси должны дополнительно характеризоваться показателем чистоты данной смеси по крупности или однородности смеси.
Показатель чистоты смеси
,
характеризующейся крупностью
,
равен:
, (4.3)
где 
– количество смеси;
– количество единиц продукта, оставшегося
на сите.
Таким образом, наиболее полная характеристика смеси по крупности и чистоте или однородности выразится так:
, (4.4)
где 
– условный показатель крупности и
чистоты;
– размер отверстий сита, через которое смесь прошла, мм;
– размер отверстий сита, с которого
смесь сошла, мм;
– показатель чистоты, равный отношению количества сходового продукта к количеству всей смеси, выраженный в процентах или долях единицы.
Пример: Навеска (200 г) продукта, полученного после сортирования проходом через сито с отверстиями диаметром 1,06 мм и сходом с сита с отверстиями диаметром 0,57 мм производственного рассева, была последовательно просеяна на лабораторных ситах с отверстиями диаметром: 1,06; 0,92; 0,83; 0,74; 0,67; 0,62; 0,57; 0,52; 0,49; 0,46; 0,42; 0,40; 0,38; 0,35; 0,33; 0,32; 0,31 мм.
По полученным данным строим интегральную кривую остатков. По оси абсцисс откладываем крупность, характеризуемую размером отверстий в миллиметрах, по оси ординат – суммарный выход классов крупности в процентах. При этом на ординате слева отложены суммы величин выхода, оставшихся на сите, справа – прошедшие через отверстия этого же сита (рисунок 4.5).
Каждая точка на этой кривой показывает зависимость между крупностью и суммарным выходом верхнего (крупного) или нижнего (мелкого) продукта. Кривая такого ситового анализа дает наглядное представление о распределении частиц по крупности.
Как видим, в исследуемой смеси оказалось 29,4 % частиц крупностью менее 0,57 мм, что указывает на недосев.
Следовательно, рассматриваемый продукт не представляет собой фракции в чистом виде. Чистота указанного продукта (фракции) характеризуется числом 70,6 %, которое соответствует ординате аМ, т.е. мы имеем смесь, в состав которой входит только 70,6 % чистого продукта – схода с сита 0,57 мм.
Рисунок 4.5 – Интегральная кривая остатков
Таким образом, для
полной характеристики данной смеси,
кроме
,
необходимо добавить и показатель чистоты
или однородности смеси, т.е. полная
характеристика этого продукта будет:
.
Часто на практике степень крупности массы частиц (или степень их измельчения) характеризуется остатком на сите. Этот остаток можно выразить в процентах, принимая все количество продукта за 100 %. Кривая остатков на ситах с разными отверстиями отмечена на рисунке 4.4 буквой Н, а связанная с ней кривая прошедшего сквозь сито продукта – буквой П.
Очевидно, что сумма оставшегося на данном сите продукта Нх и прошедшего сквозь сито Пх равна 100 %, т.е.
, (4.5)
где х – размер ячейки (размер признака, по которому происходит сортировка).
Таким образом,
или 
. (4.6)
Так как кривая прохода П является интегральной кривой по отношению к кривой распределения Р, т.е. каждая ордината этой кривой Пх есть сумма всех предыдущих ординат кривой Р, то
, (4.7)
где 
– ордината (частота повторения в
процентах);
– абсцисса кривой распределения.
Остаток же на сите для данной абсциссы будет
, (4.8)
где а – максимальное значение .
Количество продукта,
обладающего признаком
в пределе между
и
,
будет
. (4.9)
Среднее значение размеров группы частиц можно определить по кривой остатков, даже не имея в своем распоряжении кривой распределения Р. Для этого надо определить площадь кривой остатков (заключающейся между кривой, осью ординат и осью абсцисс), которая может быть представлена таким интегралом:
.
(4.10)
Так как
и
,
то
.
(4.11)
Здесь
представляет собой элементарную площадку
кривой распределения, принадлежащую
данному размеру частиц. Умножив эту
площадку на размер частицы
,
получим момент площадки относительно
оси ординат. Интеграл же представляет
собой статический момент площади кривой
распределения относительно оси ординат.
Разделив на площадь кривой, которая
равна 100 %, получим положение ординаты,
проходящей через центр тяжести площади:
.
(4.12)
Существует еще несколько других способов определения средних размеров.
В представленном на рисунке 4.4 распределении максимальная ордината сдвинута относительно медианы и линии центра тяжести влево. Такое распределение имеет левую асимметрию. При симметричном распределении (гауссова кривая) эти три ординаты совпадают (рисунок 4.6). Возможны распределения с правой асимметрией. Следующие диаграммы этого же рисунка изображают такие типы распределения: 2 – с максимумом, 3 – без максимума, 4 – с минимумом, 5 – с минимумом и максимумом, 6 – с двумя максимумами и минимумом. Пунктиром нанесены кривые остатков.
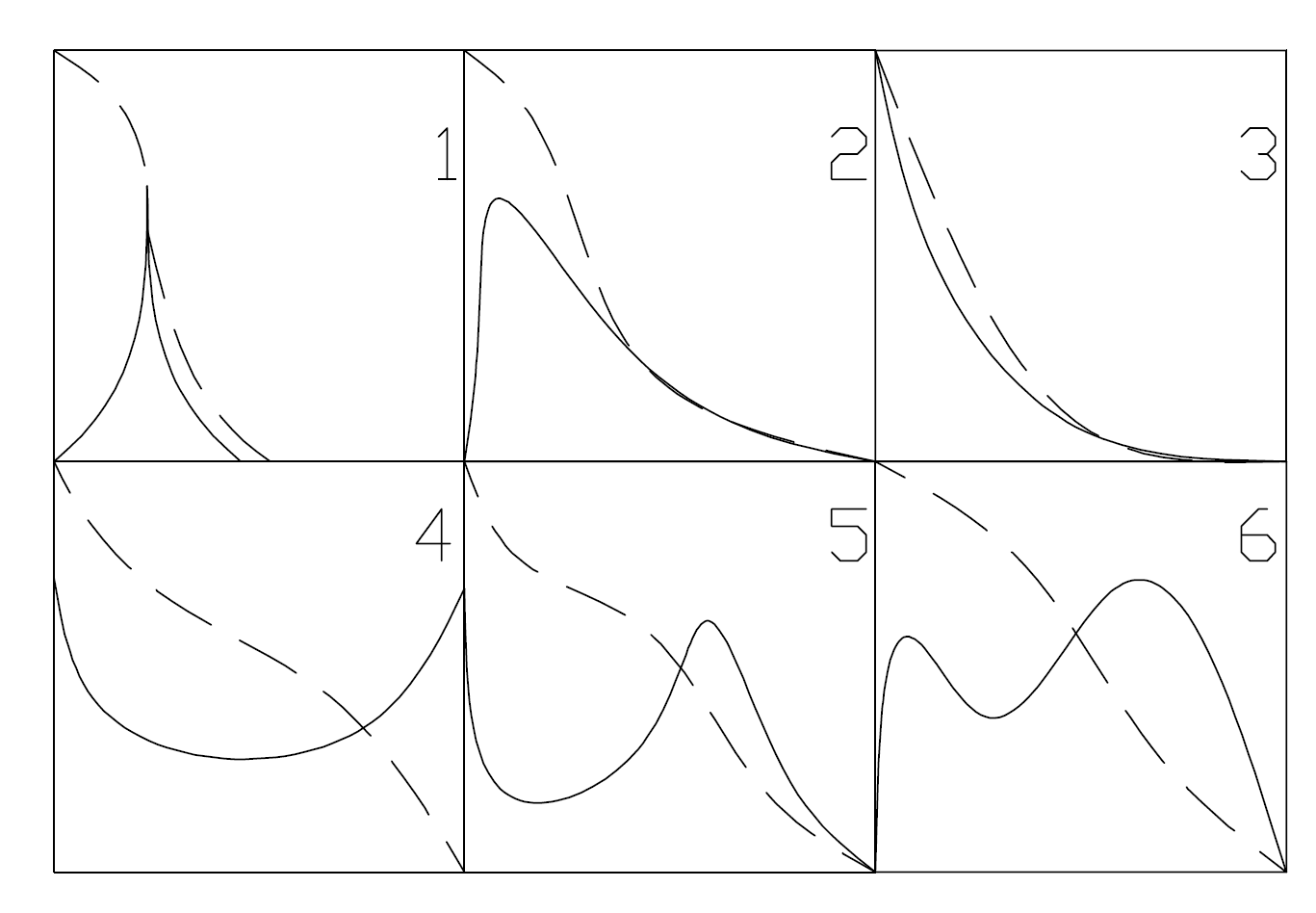
1 – гауссова кривая, 2 – с максимумом, 3 – без максимума, 4 – с минимумом, 5 – с минимумом и максимумом, 6 – с двумя максимумами и минимумом
Рисунок 4.6 – Различные типы кривых распределения и кривых остатков (пунктиром)
Кривые измельченных мельничных продуктов в большинстве случаев подходят к типам 1, 2 и 3. Примерные размеры муки (Розин и Раммлер) представлены в таблице 4.9.
Таблица 4.9 – Примерные размеры муки
Мука |
Остаток на сите, % |
Медиана, мкм |
Средний размер, мкм |
Удельная площадь частиц м2/кг |
Ржаная |
3,3 |
63,5 |
63,7 |
69,4 |
Пшеничная: - крупчатка - средняя - мелкая |
90,9 74,7 6,3 |
144 118 57,2 |
148 115 62 |
32,7 42,2 70,9 |
Интересно отметить, что размер зерен крахмала, который содержится в пшенице, лежит в пределах 50÷70 мкм.
Розин и Раммлер, рассматривая зерновое распределение продуктов измельчения как статистическую совокупность, нашли, что кривые распределения по данным ситовых анализов могут быть выражены уравнением
,
(4.13)
где 
– остаток на сите, %;
– размер частиц, мкм;
и
– постоянные, легко определяемые в
логарифмической форме по опытным данным.
Из уравнения (4.13) следует, что плотность
распределения массы по диаметрам
определяется формулой
.
(4.14)
Если
,
то при
плотность распределения
стремится к бесконечности, хотя функция
при
остается конечной. Поэтому при
формула (4.13) не дает правильного описания
распределения мелких фракций.
Беннет предложил в формуле Розина – Раммлера ввести
,
(4.15)
где 
– новый параметр.
В таком случае уравнение (4.13) примет вид
,
(4.16)
где
.
Соответственно
.
(4.17)
При
%;
(4.18)
.
(4.19)
Таким образом, по своему физическому смыслу представляет собой такой диаметр, при котором масса частиц крупнее составляет 36,8 %, а мельче – 63,2 %.
Показатель степени п в формулах (4.13), (4.16), (4.17) характеризует ширину распределения, т.е. степень однородности материала по размерам частиц: чем больше п, тем уже материал по диапазону размеров частиц.
Формула Розина – Раммлера подобрана на основании кривых Пирсона, оказавшихся наиболее подходящими для выражения функциональных зависимостей, установленных из опыта.
Формула Розина – Раммлера не является универсальной, а лишь приближенной, но применима при многих способах измельчения.
Для практического применения формулы Розина – Раммлера показательное уравнение (4.16) дважды логарифмируется:
,
или
,
(4.20)
где 
.
Это уравнение описывает прямую в
координатах
,
,
т.е. в двойной логарифмической координатной
сетке. Параметр п приобретает
значение тангенса угла наклона прямой.
Для облегчения построения двойной логарифмической координатной сетки можно воспользоваться приведенными в таблице 4.10 значениями .
Таблица 4.10– Значения для суммарных остатков Нх
Нх, % |
|
Разность |
Нх, % |
|
Разность |
1 |
2 |
3 |
1 |
2 |
6 |
0,5 |
+0,3619 |
0,0000 |
80 |
-1,0137 |
1,3756 |
1 |
+0,3010 |
0,0609 |
85 |
-1,1524 |
1,5143 |
2 |
+0,2302 |
0,1317 |
90 |
-1,3400 |
1,7019 |
5 |
+0,1142 |
0,2477 |
92 |
-1,4409 |
1,8028 |
10 |
±0,0000 |
0,3619 |
95 |
-1,6492 |
2,0111 |
20 |
-0,1555 |
0,5174 |
96 |
-1,7481 |
2,1100 |
30 |
-0,2817 |
0,6436 |
97 |
-1,8775 |
2,2394 |
40 |
-0,4002 |
0,7621 |
98 |
-2,0655 |
2,4274 |
50 |
-0,5214 |
0,8733 |
98,5 |
-2,1739 |
2,5358 |
60 |
-0,6538 |
1,0157 |
99 |
-2,3644 |
2,7263 |
70 |
-0,8097 |
1,1716 |
99,5 |
-2,6576 |
3,0195 |
75 |
-0,9027 |
1,2646 |
|
|
|
На рисунке 4.7 показано интегральное распределение частиц в двойной логарифмической координатной сетке. Для построения прямой достаточно иметь две точки, т.е. для описания распределения в двойной логарифмической координатной сетке достаточно знать остатки продукта на двух ситах.
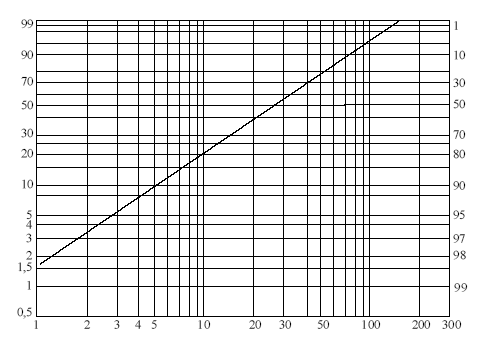
Размер частицы, мкм
Рисунок 4.7 – Интегральное распределение в двойной логарифмической
координатной сетке
Определить аналитически b и n можно из таких соображений. Для остатков на двух ситах пишем:
,
.
Логарифмируя, находим
,
.
Определяя b из одного уравнения
(4.21)
и подставляя в другое, получим:
,
(4.22)
откуда может быть определено n, а затем и b.
мкм
мкм
полный остаток
,
для частиц диаметром
–
.
Подставляя эти данные в уравнение (4.22)
,
получим
или
.
Прологарифмируя это уравнение, получим
.
Определим b из уравнения
.
.
Таким образом, уравнение остатков будет иметь вид
.
Надо сказать, что здесь везде под остатком на сите подразумевается вес всех частиц данного образца, не прошедших через данное сито, а не проход предыдущего сита, оставшийся на данном сите.