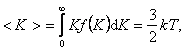Уравнение неразрывности
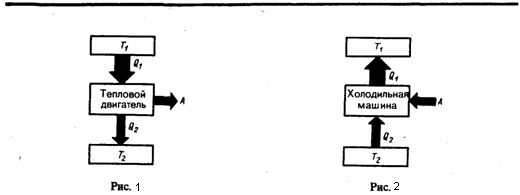
Движение жидкостей называется течением, а множество частиц движущейся жидкости - потоком. Графически движение жидкостей изображается с помощью линий тока, которые рисуются таким образом, что касательные к ним совпадают по направлению с вектором скорости жидкости в соответствующих точках пространства (рис. 1).
Рис.1
Линии тока рисуются так, чтобы густота их, которая характеризует отношение числа линий к площади перпендикулярной им площадки, через которую они проходят, была больше там, где больше скорость течения жидкости, и меньше там, где жидкость течет медленнее. Значит, по картине линий тока можно оценивать направление и модуль скорости в разных точках пространства, т. е. можно оценить состояние движения жидкости. Линии тока в жидкости можно обнаружить, например, подмешав в нее какие-либо заметные взвешенные частицы. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Течение жидкости называется установившимся (или стационарным), если расположение и форма линий тока, а также значения скоростей в каждой ее точке со временем остаются постоянными. Рассмотрим какую-либо трубку тока. Выберем два ее сечения S1 и S2, перпендикулярные направлению скорости (рис.2).
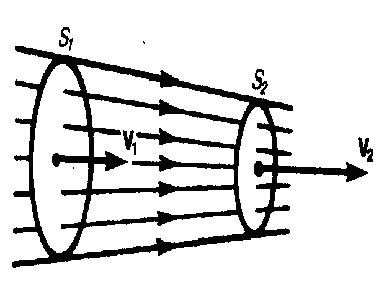
Рис.2
За время Δt через сечение S проходит объем жидкости SvΔt; следовательно, за 1 с через S1 пройдет объем жидкости S1ν1, где ν1 - скорость течения жидкости в месте сечения S1. Через сечение S1 за 1 с пройдет объем жидкости S2ν2, где ν2 - скорость течения жидкости в месте сечения S2. Мы предположили, что скорость жидкости в сечении постоянна. Если жидкость несжимаема (ρ=const), то через сечение S2 пройдет такой же объем жидкости, как и через сечение S1, т. е. S1ν1=S2ν2 (1) Следовательно, произведение скорости течения несжимаемой жидкости на поперечное сечение трубки тока есть величина постоянная для данной трубки тока. Соотношение (1) называется уравнением неразрывности для несжимаемой жидкости.
Уравнение Бернулли
Выделим в стационарно текущей идеальной жидкости (физическая модель - воображаемая жидкость, в которой нет сил внутреннего трения) трубку тока, которая ограничена сечениями S1 и S2, (рис. 1). Пусть в месте сечения S1 скорость течения ν1, давление p1 и высота, на которой это сечение расположено, h1. Аналогично, в месте сечения S2 скорость течения ν2, давление p2 и высота сечения h2.
Рис.1
За бесконечно малый отрезок
времени Δt жидкость двигается от сечения
S1 к сечению S1', от S2
к S1'.
По закону сохранения
энергии, изменение полной энергии E2-E1
идеальной несжимаемой жидкости равно
работе А внешних сил по перемещению
массы m жидкости:
(1)
где E1 и E2 - полные
энергии жидкости массой m в местах
сечений S1 и S2
соответственно.
С другой стороны,
А - это работа, которая совершается при
перемещении всей жидкости, расположенной
между сечениями S1 и S2,
за рассматриваемый малый отрезок времени
Δt. Чтобы перенести массу m от S1
до S1' жидкость должна
переместиться на расстояние l1=ν1Δt
и от S2 до S1' - на
расстояние l2=ν2Δt.
Отметим, что l1 и l2
настолько малы, что всем точкам объемов,
закрашенных на рис. 1, приписывают
постоянные значения скорости ν, давления
р и высоты h. Следовательно,
(2)
где F1 = p1S1
и F2 = -p2S2
(отрицательна, так как направлена в
сторону, противоположную течению
жидкости; рис. 1).
Полные энергии
E1 и E2 будут складываться из
кинетической и потенциальной энергий
массы m жидкости:
(3)
(4)
Подставляя (3) и (4) в (1) и приравнивая
(1) и (2), получим
(5)
Согласно уравнению неразрывности
для несжимаемой жидкости, объем,
занимаемый жидкостью, всегда остается
постоянным, т. е.
Разделив
выражение (30.5) на ΔV, получим
где
ρ - плотность жидкости. Поскольку сечения
выбирались произвольно, то
(6)
Выражение (6) получено швейцарским
физиком Д. Бернулли (1700-1782; опубликовано
в 1738 г.) и называется уравнением
Бернулли. Из его вывода видно, что
уравнение Бернулли - форма закона
сохранения энергии применительно к
установившемуся течению идеальной
жидкости. Уравнение хорошо выполняется
и для реальных жидкостей, для которых
внутреннее трение не очень велико.
Величина р в формуле (6) называется
статическим давлением (давление
жидкости на поверхность обтекаемого
ею тела), величина ρν2/2 - динамическим
давлением, величина ρgh - гидростатическое
давление.
Для горизонтальной
трубки тока (h1=h2)
выражение (6) будет вид
(7)
где p+ρν2/2 называется полным
давлением.
Из уравнения Бернулли
(7) для горизонтальной трубки тока и
уравнения неразрывности видно, что при
течении жидкости по горизонтальной
трубе, которая имеет различные сечения,
скорость жидкости больше в более узких
местах, а статическое давление больше
в более широких местах, т. е. там, где
скорость меньше. Это можно увидеть,
установив вдоль трубы ряд манометров
(рис. 2).
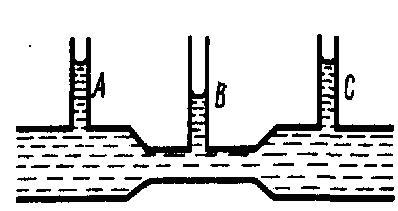
Рис.2
Данный опыт показывает, что в манометрической трубке В, которая прикреплена к узкой части трубы, уровень жидкости ниже, чем в манометрических трубках А и С, которые прикрепленны к широкой части трубы, что соответствует уравнению Бернулли. Так как динамическое давление зависит от скорости движения жидкости (газа), то уравнение Бернулли позволяет измерять скорость потока жидкости. Для этого применяется трубка Пито - Прандтля (рис. 3), состоящая из двух изогнутых под прямым углом трубок, с присоединенными к манометру противоположными концами.
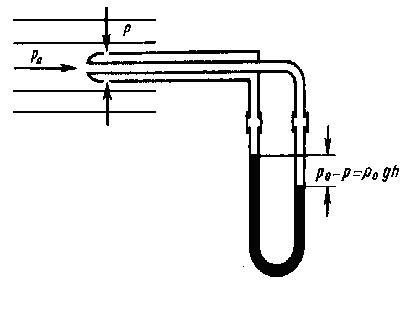
Рис.3
С помощью одной из трубок измеряется
полное давление (р0), с помощью
другой - статическое (р). С помощью
манометра измеряют разность давлений:
(8)
где ρ0 - плотность жидкости
в манометре. С другой стороны, согласно
уравнению Бернулли, разность полного
и статического давлений равна динамическому
давлению:
(9)
Из формул (8) и (9) получаем искомую
скорость потока жидкости:
Уменьшение
статического давления в точках, где
скорость потока больше, положено в
основу работы водоструйного насоса
(рис. 4). Струя воды подается в трубку,
которая открыта в атмосферу, значит
давление на выходе из трубки равно
атмосферному. В трубке сделано сужение,
по которому вода течет с большей
скоростью. В данном месте давление
меньше атмосферного. Такое же давление
деалется и в откачанном сосуде, связанным
с трубкой через разрыв, сделанный в ее
узкой части. Воздух переносится вытекающей
с большой скоростью водой из узкого
конца. Таким способом можно откачивать
воздух из сосуда до давления 100 мм рт.
ст. (1 мм рт. ст. =133,32 Па).
Рис.4
Уравнение Бернулли также используют для нахождения скорости истечения жидкости через отверстие в стенке или дне сосуда. Рассмотрим цилиндрический сосуд с жидкостью,с маленьким отверстием в боковой стенке на некоторой глубине ниже уровня жидкости (рис. 5).
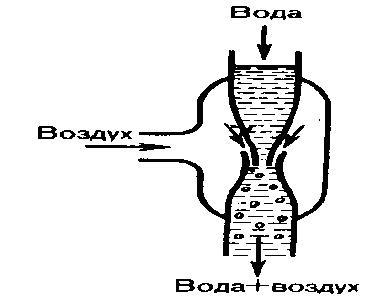
Рис.5
Рассмотрим два сечения (на уровне
h1 свободной поверхности
жидкости в сосуде и на уровне h1
выхода ее из отверстия) и применим
уравнение Бернулли:
Так
как давления р1 и р2 в жидкости
на уровнях первого и второго сечений
равны атмосферному, т. е. р1=р2,
то уравнение будет иметь вид
Из
уравнения неразрывности мы знаем, что
ν2/ν2=S1/S2,
где S1 и S2 - площади
поперечных сечений сосуда и отверстия.
Если S1>>S2, то
слагаемым ν12/2 можно
пренебречь и
Это
выражение получило название формулы
Торричелли.
10) С точки зрения термодинамики под внутренней энергией тела понимают сумму кинетической энергии хаотического движения составляющих ее частиц и потенциальной энергии их взаимодействия.
Понятие теплоемкости. Дадим определение теплоемкости.
Теплоемкость системы численно равна количеству теплоты, которое необходимо сообщить системе, чтобы ее температура увеличилась на 1 Кельвин.
Следовательно, теплоемкость системы C равна C = dQ/dT.
Количество теплоты, необходимое для нагревания 1 моля вещества на 1 Кельвин, называется молярной теплоемкостью C = dQ/(·dT).
Количество теплоты, необходимое для нагревания 1 килограмма вещества на 1 Кельвин, называется удельной теплоемкостью c = dQ/(m·dT).
Молярная теплоемкость легко рассчитать, зная значение удельной теплоемкости и молярную массу
C = с·.
Понятие теплоемкости. Дадим определение теплоемкости.
Теплоемкость системы численно равна количеству теплоты, которое необходимо сообщить системе, чтобы ее температура увеличилась на 1 Кельвин.
Следовательно, теплоемкость системы C равна C = dQ/dT.
Количество теплоты, необходимое для нагревания 1 моля вещества на 1 Кельвин, называется молярной теплоемкостью C = dQ/(·dT).
Количество теплоты, необходимое для нагревания 1 килограмма вещества на 1 Кельвин, называется удельной теплоемкостью c = dQ/(m·dT).
Молярная теплоемкость легко рассчитать, зная значение удельной теплоемкости и молярную массу
C = с·.
Термодинамические процессы, при которых теплоемкость остается постоянной называются политропными.
Итак, средняя энергия приходящаяся на одну степень свободы:
|
|
|
(4.4.1) |
У одноатомной молекулы i = 3, тогда для одноатомных молекул
|
|
|
(4.4.2) |
для двухатомных молекул
|
|
|
(4.4.3) |
для трёхатомных молекул
|
|
|
(4.4.4) |
Таким образом, на среднюю кинетическую энергию молекулы, имеющей i-степеней свободы, приходится
|
|
|
(4.4.5) |
Это и есть закон Больцмана о равномерном распределении средней кинетической энергии по степеням свободы.
11) Теплоемкость при постоянном объеме. В зависимости от того, какой параметр системы остается постоянным при протекании процесса, вводят понятия теплоемкости при постоянном объеме и давлении. Запишем первое начало термодинамики (13.3) для одного моля газа, воспользовавшись определением молярной теплоемкости и выражением для расчета элементарной работы (13.4).
C·dT = dU + P·dV. (13.6)
Если газ нагревается при постоянном объеме, то работа, совершаемая газом, равняется нулю и сообщаемая ему извне теплота идет на увеличение внутренней энергии газа. Следовательно, молярная теплоемкость при постоянном объеме Cv равна:
Cv = dU/dT. (13.7)
Молярная теплоемкость при постоянном объеме равна изменению внутренней энергии одного моля газа при его изохорическом нагревании на 1 Кельвин.
Как будет показано в дальнейшем, величина изменения внутренней энергии 1 моля идеального газа dU равна:
dU = i·R·dT/2, где i - число степеней свободы; R - универсальная газовая постоянная.
Следовательно, Cv = i·R/2. (13.8)
Теплоемкость при постоянном давлении. Уравнение Майера. В случае нагревания газа при постоянном давлении выражение (13.6) можно записать в виде:
Cp = dUm/dT + P·dVm/dT.
Воспользовавшись уравнением Менделеева-Клапейрона и выражением (13.7), получим, что
Cp = Cv + R. (13.9)
Выражение (13.9) называется уравнением Майера. Оно показывает, что расширение моля идеального газа при постоянном давлении и изменении его температуры на 1 Кельвин требует дополнительного, по сравнению с изобарическим расширением, количества теплоты, необходимого для совершения работы. Это значение равно универсальной газовой постоянной.
Воспользовавшись выражением (13.8), получим
Cp = (i + 2)·R/2. (13.10)
Коэффициент Пуассона Как видно из выражения 13.10 отношение теплоемкостей при постоянном давлении и объеме, называемое коэффициентом Пуассона, определяется только числом степеней свободы атомов или молекул и не зависит явным образом от температуры.
g = Cp/Cv = (i + 2)/i. (13.11)
Заметим, что температурная зависимость коэффициента g не проявляется только для одноатомных газов. Для многоатомных молекул число степеней свободы скачкообразно увеличивается с ростом температуры, т.к. при этом происходит увеличение степеней свободы частиц. В области низких температур существует только поступательное движение молекул i = iп = 3, далее - в области более высоких температур к ним добавляются степени свободы, связанные с возможностью вращательного движения, i = iп+ iвр, а затем - колебательного движения i = iп+ iвр + 2·iк.
Число
степеней свободы i равно числу независимых
координат, однозначно определяющих
положение тела (или молекулы) в
пространстве.
Расчет внутренней энергии и количества теплоты при изохорическом процессе. Исходя из выражения для расчета работы (13.4), очевидно, что в данном процессе газ работы не совершает. Следовательно, согласно первому началу термодинамики (13.3) и выражению для молярной теплоемкости (13.7)
для произвольной массы реального газа при изохорическом процессе изменение его внутренней энергии равно количеству сообщенной ему теплоты:
dU = Q = (m/)·Cv·dT. (13.12)
Обратите внимание, что для идеального газа выражение (13.12) окажется справедливым для расчета изменения внутренней энергии для любых процессов. Действительно, поскольку изменение внутренней энергии обусловлено только изменением кинетической энергии частиц ТС (температурой), а потенциальная энергия их взаимодействия при любом состоянии газа равна нулю, то дополнительный фактор, связанный с изменением объема (расстояния между частицами), не приведет к изменению выражения для расчета величины dU.
Для идеального газа dU = (m/)·Cv·dT (13.13) для любых термодинамических процессов.
Итак, внутренняя энергия идеального газа зависит только от температуры.
Пример. Опыт Гей-Люссака и Джоуля. При адиабатическом расширении идеального газа в пустоту внутренняя энергия, а, следовательно, и температура не зависят от объема сосуда, в котором находится газ.
Расчет работы и количества теплоты при изобарическом процессе. Для изобарического процесса работа газа при произвольном изменении его объема равна
A1-2 = P·(V2 - V1). (13.14)
Подставив в (13.14) выражение для расчета объема через давление и температуру, полученное из уравнения Менделеева-Клапейрона, будем иметь, что
A1-2 = (m/)·R·(T2 - T1). (13.15)
Количество теплоты сообщенное или отведенное от газа будет равно:
Q = Cp·dT.
Эта теплота идет на совершение работы и изменение внутренней энергии, равной dU = (m/)·Cv·dT.
Из выражения (13.15) следует физический смысл универсальной газовой постоянной.
Универсальная газовая постоянная численно равна работе, которую совершает один моль идеального газа при изобарическом расширении и изменении температуры на 1 К.
асчет работы и количества теплоты при изотермическом процессе. Работа газа при произвольном изменении его объема равна:
. (13.16)
Подставив в (13.16) выражение для расчета давления через объем итемпературу, полученное из уравнения Менделеева-Клапейрона, будем иметь, что для изотермического процесса:
A1-2 = (m/)·R·T·ln(p1/p2). (13.17)
Изменение внутренне энергии при изотермическом процессе равняется нулю dU = 0, следовательно, исходя из первого начала термодинамики, все количество теплоты идет на совершение газом работы Q = A и
Q1-2 = A1-2 = (m/)·R·T·ln(p1/p2).
Уравнение адиабаты (уравнение Пуассона). Адиабатическим называется процесс, происходящий без теплообмена с окружающей средой. Следовательно, для него характерно наличие хорошей изоляции ТС от внешней среды или высокая скорость термодинамического процесса, при которой теплообмен незначителен.
Примеры адиабатных процессов: работа двигателей внутреннего сгорания; процессы, происходящие в термостатах; разряжение и сжатие газа при распространении звуковой волны.
Поскольку обратимые процессы, в отличии от адиабатных, являются бесконечно медленными, то о равновесности последних можно говорить только применительно к определенным областям ТС.
Поскольку для адиабатического процесса Q = 0, то A = - dU. Следовательно,
p·dV = - (m/)·Cv·dT. (13.18)
Следовательно, работа газа при адиабатическом расширении равна
A1-2 = (m/)·Cv·(T1 - T2). (13.19)
Выразив величину P из уравнения Менделеева-Клапейрона и подставив ее в (13.18), после соответствующих преобразований получим уравнение адиабаты:
T·V-1 = const или p·V = const. (13.20)
Уравнение (13.20) называется также уравнением Пуассона.
На диаграмме P-V адиабата испытывает более резкое падание, чем изотерма (см. рис. 13.4), т.е. в любой точке кривой модуль производной от давления по объему для нее больше. Действительно, из уравнения адиабаты можно показать, что
dp/dV = - ·p/V > p/V.
Уравнение политропы. Рассмотренные выше изохорический, изобарический, изотермический и адиабатический процессы обладают одним общим свойством - имеют постоянную теплоемкость.
12) ри выводе основного уравнения молекулярно-кинетической теории газов и максвелловского распределения молекул по скоростям делалось предположение, что внешние силы не действуют на молекулы газа, поэтому молекулы равномерно распределены по объему. Но молекулы любого газа находятся в потенциальном поле тяготения Земли. Сила тяжести, с одной стороны, и тепловое движение молекул — с другой, приводят газ к некоторому стационарному состоянию, при котором давление газа с высотой уменьшается. Выведем закон изменения давления с высотой, предполагая при этом, что масса всех молекул одинакова, поле тяготения однородно и температура постоянна.
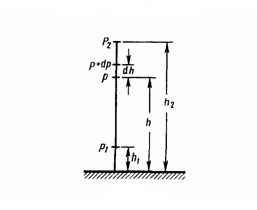
Рис.1
Если атмосферное давление на
высоте h равно р (рис. 1), то на высоте h+dh
оно равно p+dp (при dh>0 dp<0, так как
давление с высотой уменьшается). Разность
давлений р и p+dp равна весу газа,
заключенного в объеме цилиндра высотой
dh с основанием площадью 1 м2:
где
ρ — плотность газа на высоте h (dh настолько
мало, что при изменении высоты в этом
интервале плотность газа можно считать
постоянной). Значит,
(1)
Зная уравнение состояния идеального
газа pV=(m/M) RT (m — масса газа, М — молярная
масса газа), находим, что
Подставив
это выражение в (1), получим
или
С
изменением высоты от h1 до h2
давление изменяется от р1 до р2
(рис. 67), т. е.
или
(2)
Выражение (2) называется
барометрической формулой. Она
позволяет вычислить атмосферное давление
в зависимости от высоты или, измеряя
давление, найти высоту: Так как высоты
считаются относительно уровня моря,
где давление считается нормальным, то
выражение (2) может быть представлено в
виде
(3)
где р — давление на высоте h.
Прибор для определения высоты
над земной поверхностью называется
высотомером (или альтиметром).
Его работа основана на применении
формулы (3). Из этой формулы следует, что
чем тяжелее газ, тем давление с высотой
убывает тем быстрее.
Барометрическую
формулу (3) можно преобразовать, если
воспользоваться формулой p=nkT:
где
n – концентрация молекул на высоте h, n0
– то же, на высоте h=0. Так как M=m0NA
(NA – постоянная Авогадро, m0
– масса одной молекулы), a R=kNA, то
(4)
где m0gh=P — потенциальная
энергия молекулы в поле тяготения, т.
е.
(5)
Выражение (5) называется
распределением Больцмана для
внешнего потенциального поля. Из него
видно, что при постоянной температуре
плотность газа больше там, где меньше
потенциальная энергия его молекул.
Если частицы находятся в состоянии
хаотического теплового движения и имеют
одинаковую массу и , то распределение
Больцмана (5) применимо в любом внешнем
потенциальном поле, а не только в поле
сил тяжести.
|
В п. 2.3 мы получили выражение для распределения молекул по скоростям (распределение Максвелла):
Из этого выражения
легко найти распределение молекул
газа по значениям кинетической энергии
K. Для этого перейдём от переменной
υ к переменной
где dn(K) – число молекул, имеющих кинетическую энергию поступательного движения, заключённую в интервале от K до K+dK. Отсюда получим функцию распределения молекул по энергиям теплового движения:
Средняя кинетическая энергия молекулы идеального газа:
то есть получаем результат, совпадающий с прежним результатом, полученным в п. 1.3. Итак, закон Максвелла даёт распределение частиц по значениям кинетической энергии, а закон Больцмана – распределение частиц по значениям потенциальной энергии. Оба распределения можно объединить в единый закон Максвелла – Больцмана:
Здесь n0 – число молекул в единице объёма в той точке, где U = 0, E = U+K – полная энергия. В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия Е, могут принимать непрерывный ряд значений. Если же энергия частицы может принимать лишь дискретный ряд значений Е1, Е2…, (как это имеет место, например, для внутренней энергии атома), то в этом случае распределение Больцмана имеет вид:
где Ni – число частиц, находящихся в состоянии с энергией Ei , а A> – коэффициент пропорциональности, который должен удовлетворять условию
где N – полное число частиц в рассматриваемой системе. Тогда окончательное выражение распределения Максвелла – Больцмана для случая дискретных значений энергий будет иметь вид:
|
:
.
,
13)
|
|
|
|
|
(1)
где jE — плотность
теплового потока — величина,
которая определяется энергией,
переносимой в форме теплоты в единицу
времени через единичную площадку,
перпендикулярную оси х, λ —
теплопроводность, — градиент
температуры, равный скорости изменения
температуры на единицу длины х в
направлении нормали к этой площадке.
Знак минус говорит о том, что во время
теплопроводности энергия перемещается
в направлении убывания температуры
(поэтому знаки jE и –
противоположны). Теплопроводность
λ равна плотности теплового потока
при градиенте температуры, равном
единице.
Можно показать, что
(2)
где сV — удельная
теплоемкость газа при постоянном
объеме (количество теплоты, которое
необходимо для нагревания 1 кг газа
на 1 К при постоянном объеме), ρ —
плотность газа, <ν> — средняя
скорость теплового движения молекул,
<l> — средняя длина свободного
пробега.
2. Диффузия. При
происходит самопроизвольное
проникновение и перемешивание частиц
двух соприкасающихся газов, жидкостей
и даже твердых тел; диффузия есть
обмен масс частиц этих тел, при этом
явление возникает и продолжается,
пока существует градиент плотности.
Во времена становления
молекулярно-кинетической теории по
вопросу явления диффузии возникли
противоречия. Поскольку молекулы
перемещаются в пространстве с
огромными скоростями, то диффузия
должна происходить очень быстро.
Если же открыть в комнате крышку
сосуда с пахучим веществом, то запах
распространяется довольно медленно.
Но здесь нет противоречия. При
атмосферном давлении молекулы
обладают малой длиной свободного
пробега и, при столкновениях с другими
молекулами, приемущественно «стоят»
на месте.
Явление диффузии
для химически однородного газа
подчиняется закону Фика:
(3)
где jm — плотность
потока массы — величина, определяемая
массой вещества, диффундирующего в
единицу времени через единичную
площадку, перпендикулярную оси х, D
— диффузия (коэффициент
диффузии), dρ/dx — градиент плотности,
который равен скорости изменения
плотности на единицу длины х в
направлении нормали к этой площадке.
Знак минус говорит о том, что перенос
массы происходит в направлении
убывания плотности (поэтому знаки
jm и dρ/dx противоположны). Диффузия
D численно равна плотности потока
массы при градиенте плотности, равном
единице. Согласно кинетической
теории газов,
(4)
3. Внутреннее трение
(вязкость). Суть механизма
возникновения внутреннего трения
между параллельными слоями газа
(жидкости), которые движущутся с
различными скоростями, есть в том,
что из-за хаотического теплового
движения осуществляется обмен
молекулами между слоями, в результате
чего импульс слоя, который движется
быстрее, уменьшается, который движется
медленнее — увеличивается, что
приводит к торможению слоя, который
движется быстрее, и ускорению слоя,
который движется медленнее.
Как
известно, сила внутреннего трения
между двумя слоями газа (жидкости)
подчиняется закону Ньютона:
(5)
где η — динамическая вязкость
(вязкость), dν/dx — градиент
скорости, который показывает быстроту
изменения скорости в направлении
х, перпендикулярном направлению
движения слоев, S — площадь, на которую
действует сила F.
Согласно
второму закону Ньютона взаимодействие
двух слоев можно рассматривать как
процесс, при котором в единицу времени
от одного слоя к другому передается
импульс, который по модулю равен
действующей силе. Тогда выражение
(5) можно записать в виде
(6)
где jp — плотность
потока импульса — величина, которая
определяется определяемая полным
импульсом, переносимым в единицу
времени в положительном направлении
оси х через единичную площадку,
перпендикулярную оси х, dν/dx —
градиент скорости. Знак минус говорит
о том, что импульс переносится в
направлении убывания скорости
(поэтому знаки jp и dν/dx
противоположны).
Динамическая
вязкость η численно равна плотности
потока импульса при градиенте
скорости, равном единице; она
вычисляется по формуле
(7)
Из сопосавления формул (1), (3)
и (6), которые описывают явления
переноса, следует, что закономерности
всех явлений переноса сходны между
собой. Эти законы были известны еще
задолго до того, как они были обоснованы
и получены из молекулярно-кинетической
теории, которая позволила установить,
что внешнее сходство их математических
выражений является следствием
общностью лежащего в основе явлений
теплопроводности, диффузии и
внутреннего трения молекулярного
механизма перемешивания молекул в
процессе их хаотического движения
и столкновений друг с другом.
Рассмотренные законы Фурье,
Фика и Ньютона не вскрывают
молекулярно-кинетической сути
коэффициентов λ, D и η. Выражения для
коэффициентов переноса получаются
из кинетической теории. Они записаны
без вывода, поскольку строгое и
формальное рассмотрение явлений
переноса довольно громоздко, а
качественное — не имеет смысла.
Формулы (2), (4) и (7) дают связь
коэффициентов переноса и характеристики
теплового движения молекул. Из этих
формул следуют простые зависимости
между λ, D и η:
и
Используя
эти формулы, можно по найденным из
опыта одним величинам найти другие.
|
|
|
|
|
Для
определения < z > представим себе
молекулу в виде шарика диаметром d,
которая движется среди других как
бы застывших молекул. Эта молекула
столкнется только с теми молекулами,
центры которых находятся на
расстояниях, равных или меньших d,
т. е. лежат внутри так называемого
ломаного цилиндра радиусом d (рис.
2).
Среднее число столкновений
за 1 с равно числу молекул в объеме,
так называемого ломаного цилиндра:
где
n — концентрация молекул, V = πd2<v>
,где <v> — средняя скорость молекулы
или путь, пройденным ею за 1 с). Таким
образом, среднее число столкновений
Расчеты
показывают, что при учете движения
других молекул
Тогда
средняя длина свободного пробега
т.
е. <l> обратно пропорциональна
концентрации n молекул. С другой
стороны, p=nkt. Значит,
14)
|
|
|
|
|
(1)
т. е. работа, которая совершается
за цикл, равна количеству теплоты,
полученной извне. Однако в результате
кругового процесса система может
теплоту как получать, так и отдавать,
поэтому
где
Q1 — количество теплоты, которая
получила система, Q2 — количество
теплоты, которое отдала система.
Поэтому термический коэффициент
полезного действия для кругового
процесса
(2)
Термодинамический процесс
называется обратимым, если он
может осуществляться как в прямом,
так и в обратном направлении, причем
если такой процесс осуществляется
сначала в прямом, а затем в обратном
направлении и система возвращается
в первоначальное состояние, то в
окружающей среда и в этой системе
не происходит никаких изменений.
Всякий процесс, не удовлетворяющий
этим условиям, является необратимым.
Любой равновесный процесс
является обратимым. Обратимость
равновесного процесса, который
происходит в системе, следует из
того, что любое промежуточное
состояние является состоянием
термодинамического равновесия; для
него не имеет значения, идет процесс
в прямом или обратном направлении.
Реальные процессы также сопровождаются
диссипацией энергии (из-за трения,
теплопроводности и т. д.), которая
здесь нами не обсуждается. Обратимые
процессы — это идеализация реальных
процессов. Их исследование важно по
двум причинам: 1) многие процессы в
природе и технике практически
обратимы; 2) обратимые процессы
являются наиболее экономичными;
имеют максимальный термический
коэффициент полезного действия
(КПД), что позволяет указать пути
повышения КПД реальных тепловых
двигателей.
|
|
|
|
|
(1)
При адиабатическом расширении
2—3 теплообмен с окружающей средой
отсутствует и работа расширения А23
делается за счет изменения внутренней
энергии:
Количество
теплоты Q2, которое отдано газом
холодильнику при изотермическом
сжатии, равно работе сжатия А34:
(2)
Работа адиабатического сжатия
Работа,
совершаемая в результате кругового
процесса,
и,
как можно показать, определяется
площадью, заштрихованной на рис. 87.
Термический к. п. д. цикла Карно
Применив
формулу TVγ-1=const для адиабатического
процесса 2—3 и 4—1, получим
и
откуда
(3)
Подставляя (1) и (2) в формулу
для КПД для тепловогот процесса и
учитывая (3), получаем
(4)
т. е. для цикла Карно КПД
действительно определяется только
температурами нагревателя и
холодильника. Для повышения КПД
нужно увеличивать разность температур
нагревателя и холодильника. Например,
при T1 = 400 К и T2 = 300 К η =
0,25. Если же температуру нагревателя
повысить на 100 К, а температуру
холодильника понизить на 50 К, то η =
0,5. КПД всякого реального теплового
двигателя из-за действыующего трения
и неизбежных тепловых потерь гораздо
меньше вычисленного для цикла Карно.
Обратный цикл Карно
применяется при проектировании
тепловых насосов. В отличие от
холодильных машин тепловые насосы
должны как можно больше тепловой
энергии отдавать горячему телу,
например системе отопления. Часть
этой энергии отбирается от окружающей
среды с более низкой температурой,
а часть — получается за счет
механической работы, производимой,
например, компрессором.
Теорема
Карно также стала основанием для
установления термодинамической
шкалы температур. Сравнив левую и
правую части формулы (4), получим
(5)
т. е. для сравнения температур
Т1 и T2 двух тел необходимо
произвести обратимый цикл Карно, в
котором одно тело используется как
нагреватель, другое как холодильник.
Из равенства (5) мы видим, что отношение
температур тел равно отношению
отданного в этом цикле количества
теплоты к полученному. По теореме
Карно, химический состав рабочего
тела не влияет на результаты сравнения
температур, поэтому такая
термодинамическая шкала не связана
со свойствами какого-то конкретного
термометрического тела. Обратим
внимание, что таким образом сравнивать
температуры практически трудно, так
как реальные термодинамические
процессы, как уже говорилось, являются
необратимыми.
|
|
|
|
|
Так
как энтропия задается с точностью
до аддитивной постоянной, то эту
постоянную для простоты возьмем
равной нулю. При этом отметим, что
это произвольное допущение, т.к.
энтропия по своей сущности всегда
задается с точностью до аддитивной
постоянной. Из теоремы Нернста —
Планка следует, что теплоемкости Ср
и СV при 0 К равны нулю.
|
|
|
|
|
(1)
Из равенства нулю интеграла
(1), взятого по замкнутому контуру,
следует, что подынтегральное выражение
δQ/T есть полный дифференциал некоторой
функции, которая определяется только
состоянием системы и не зависит от
пути, которым система пришла в это
состояние. Таким образом,
(2)
Функция состояния, у которой
дифференциал равен δQ/T, называется
энтропией и обозначается S.
Из
формулы (1) следует, что для обратимых
процессов изменение энтропии
(3)
В термодинамике доказывается,
что энтропия системы, совершающей
необратимый цикл, возрастает:
(4)
Выражения (3) и (4) применяются
только к замкнутым системам, если
же система обменивается теплотой с
внешней средой, то ее энтропия может
вести себя произвольным образом.
Соотношения (3) и (4) можно представить
в виде неравенства Клаузиуса
(5)
т. е. энтропия замкнутой
системы может либо возрастать (в
случае необратимых процессов), либо
оставаться постоянной (в случае
обратимых процессов).
Если
система совершает равновесный
переход из состояния 1 в состояние
2, то, согласно (2), изменение энтропии
(6)
где подынтегральное выражение
и пределы интегрирования определяются
через величины, которые характеризуют
рассматриваемый процесс. Формула
(6) определяет энтропию лишь с точностью
до аддитивной постоянной (слагаемого).
Физический смысл имеет не сама
энтропия, а разность энтропий.
Используя выражение (6), найдем
изменение энтропии в процессах
идеального газа. Taк как dU=(m/M)CVdT,
δA=pdV=(m/M)RT(dV/V) , то
или
(7)
т. е. изменение энтропии ΔS1→2
идеального газа при переходе его из
cоcтояния 1 в cоcтояние 2 не завиcит
от вида процеccа перехода 1→2.
Так
как для адиабатического процесса
δQ = 0, то ΔS = 0 и, следовательно, S=const,
т. е. адиабатический обратимый
процесс протекает при постоянной
энтропии. Поэтому его часто называют
изоэнтропийным процессом. Из
формулы (7) следует, что при изотермическом
процессе (T1= T2)
при
изохорном процессе (V1 = V2)
Энтропия
обладает свойством аддитивности:
энтропия системы равна сумме энтропий
тел, которые входят в систему.
Свойством аддитивности обладают
также внутренняя энергия, масса,
объем (но таким свойством не обладают
температура и давление).
Более
глубокий смысл энтропии показывается
в статистической физике: энтропия
связывается с термодинамической
вероятностью состояния системы.
Термодинамическая вероятность
W состояния системы — это число
способов, с помощью которых может
быть реализовано данное состояние
макроскопической системы, или число
микросостояний, которые осуществляют
данное макросостояние (по определению,
W≥1, т. е. термодинамическая вероятность
не есть вероятность в математическом
смысле (последняя ≥1 !!!)).
Cогласно
Больцману, энтропия cиcтемы и
термодинамическая вероятность
связаны между собой следующим
образом:
(8)
где k — постоянная Больцмана.
Таким образом, энтропия определяется
логарифмом числа микросостояний, с
помощью которых может быть осуществлено
данное макросостояние. Значит,
энтропия может рассматриваться как
мера вероятности состояния
термодинамической системы. Формула
Больцмана (8) позволяет дать энтропии
следующее статистическое толкование:
энтропия является мерой
неупорядоченности системы.
Действительно, чем больше число
микросостояний, которые реализуют
данное макросостояние, тем больше
энтропия. В состоянии равновесия —
наиболее вероятного состояния
системы — число микросостояний
максимально, при этом также максимальна
и энтропия.
Так как реальные
процессы необратимы, то можно
говорить, что все процессы в замкнутой
системе ведут к увеличению ее энтропии
— принцип возрастания энтропии.
При статистическом толковании
энтропии это означает, что процессы
в замкнутой системе идут в направлении
увеличения числа микросостояний,
другими словами, от менее вероятных
состояний к более вероятным, до тех
пор пока вероятность состояния не
станет максимальной.
Соотнося
выражения (5) и (8), видим, что энтропия
и термодинамическая вероятность
состояний замкнутой системы могут
либо увеличиваться (в случае
необратимых процессов), либо оставаться
неизменными (в случае обратимых
процессов).
Отметим, однако,
что эти утверждения имеют место для
систем, которые состоят из очень
большого числа частиц, но могут
нарушаться в системах с малым числом
частиц. Для систем с малым числом
частиц могут наблюдаться флуктуации,
т. е. энтропия и термодинамическая
вероятность состояний замкнутой
системы на фиксированном отрезке
времени могут уменьшаться, а не
увеличиваться, или оставаться
постоянными.
15) .Уравнение Ван-Дер-Ваальса. Изотермы Ван-Дер-Ваальса и их анализ. Внутренняя энергия реального газа.
Ван-дер-Ваальсом в уравнение Клапейрона — Менделеева введены две поправки.
1. Учет собственного объема молекул. Наличие сил отталкивания, которые противодействуют проникновению в занятый молекулой объем других молекул, сводится к тому, что фактический свободный объем, в котором могут двигаться молекулы реального газа, будет не Vm, а Vm — b, где b — объем, занимаемый самими молекулами.
Объем b равен учетверенному собственному объему молекул. Если, например, в сосуде находятся две молекулы, то центр любой из них не может приблизиться к центру другой молекулы на расстояние, меньшее диаметра d молекулы. Это означает, что для центров обеих молекул оказывается недоступным сферический объем радиуса d, т. е. объем, равный восьми объемам молекулы или учетверенному объему молекулы в расчете на одну молекулу.
2.
Учет притяжения молекул.
Действие сил притяжения газа приводит
к появлению дополнительного давления
на газ, называемого внутренним давлением.
По вычислениям Ван-дер-Ваальса,
внутреннее давление обратно пропорционально
квадрату молярного объема, т.
е.
где а
— постоянная
Ван-дер-Ваальса, характеризующая силы
межмолекулярного притяжения,Vm — молярный
объем.
Вводя
эти поправки, получим уравнение
Ван-дер-Ваальса для
моля газа (уравнение
состояния реальных газов):
Для произвольного количества вещества v газа (v=m/M) с учетом того, что V=vVm, уравнение Ван-дер-Ваальса примет вид
где поправки а и b — постоянные для каждого газа величины, определяемые опытным путем (записываются уравнения Ван-дер-Ваальса для двух известных из опыта состояний газа и решаются относительно а и b).
Изотермы Ван-дер-Ваальса — кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые имеют довольно своеобразный характер. При высоких температурах (T > Tк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Tк на изотерме имеется лишь одна точка перегиба К.
Эта изотерма называется критической, соответствующая ей температура Tк — критической температурой; точка перегиба К называется критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем Vк, и давление рк называются также критическими. Состояние с критическими параметрами (pк, Vк, Tк) называетсякритическим состоянием. При низких температурах (Т < Tк ) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
Для
пояснения характера изотерм преобразуем
уравнение Ван-дер-Ваальса к
виду
Уравнение
при заданных р и Т является
уравнением третьей степени относительно Vm;
следовательно, оно может иметь либо три
вещественных корня, либо один вещественный
и два мнимых, причем физический смысл
имеют лишь вещественные положительные
корни. Поэтому первому случаю соответствуют
изотермы при низких температурах (три
значения объема газа V1, V2 иV3 отвечают
(символ «m»
для простоты опускаем) одному значению
давления р1), второму
случаю — изотермы при высоких
температурах.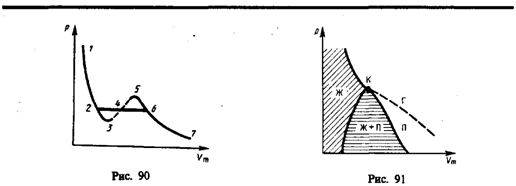 
Рассматривая различные участки изотермы при T<Тк (рис. 90), видим, что на участках 1—3 и 5—7 при уменьшении объема Vm давление р возрастает, что естественно. На участке 3—5 сжатие вещества приводит к уменьшению давления; практика же показывает, что такие состояния в природе не осуществляются. Наличие участка 3—5 означает, что при постепенном изменении объема вещество не может оставаться все время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы. Таким образом, истинная изотерма будет иметь вид ломаной линии 7—6—2—1. Часть 6–7 отвечает газообразному состоянию, а часть 2–1 — жидкому. В состояниях, соответствующих горизонтальному участку изотермы 6—2, наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.
Для нахождения критических параметров подставим их значения в уравнение
(символ «m» для простоты опускаем). Поскольку в критической точке все три корня совпадают и равны Vк уравнение приводится к виду
или 
Tax как
уравнения тождественны, то в них должны
быть равны и коэффициенты при неизвестных
соответствующих степеней. Поэтому
можно записать
Решая
полученные уравнения, найдем
Если через крайние точки горизонтальных участков семейства изотерм провести линию, то получится колоколообразная кривая (рис. 91), ограничивающая область двухфазных состояний вещества. Эта кривая и критическая изотерма делят диаграмму р,Vm под изотермой на три области: под колоколообразной кривой располагается область двухфазных состояний (жидкость и насыщенный пар), слева от нее находится область жидкого состояния, а справа — область пара. Пар отличается от остальных газообразных состояний тем, что при изотермическом сжатии претерпевает процесс сжижения. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
Сравнивая изотерму Ван-дер-Ваальса с изотермой Эндрюса (верхняя кривая на рис. 92), видим, что последняя имеет прямолинейный участок 2—6, соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния называютсяметастабильными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы.
При достаточно низких температурах изотерма пересекает ось Vm, переходя в область отрицательных давлений (нижняя кривая на рис. 92). Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются. Участок 8—9 на нижней изотерме соответствует перегретой жидкости, участок 9—10 — растянутой жидкости.
Внутренняя энергия реального газа складывается из кинетической энергии теплового движения его молекул (определяет внутреннюю энергию идеального газа, равную СVТ) и потенциальной энергии межмолекулярного взаимодействия. Потенциальная энергия реального газа обусловлена только силами притяжения между молекулами. Наличие сил притяжения приводит к возникновению внутреннего давления на газ (см. (61.1)):
Работа,
которая затрачивается для преодоления
сил притяжения, действующих между
молекулами газа, как известно из механики,
идет на увеличение потенциальной энергии
системы, т. е. 
или 
откуда
(постоянная интегрирования принята равной нулю). Знак минус означает, что молекулярные силы, создающие внутреннее давление р', являются силами притяжения. Учитывая оба слагаемых, получим, что внутренняя энергия моля реального газа
(63.1)
растет с повышением температуры и увеличением объема.
Если газ расширяется без теплообмена с окружающей средой (адиабатический процесс, т. е. Q=0) и не совершает внешней работы (расширение газа в вакуум, т. е. А=0), то на основании первого начала термодинамики (Q = (U2—U1)+ A) Получим, что
(63.2)
Следовательно, при адиабатическом расширении без совершения внешней работы внутренняя энергия газа не изменяется.
Равенство (63.2) формально справедливо как для идеального, так и для реального газов, но физический смысл его для обоих случаев совершенно различен. Для идеального газа равенство U1=U2 означает равенство температур (T1=T2), т. е. при адиабатическом расширении идеального газа в вакуум его температура не изменяется. Для реального газа из равенства (63.2), учитывая, что для моля газа
(63.3)
получаем
Так как V2> V1, то Т1 > Т2, т. е. реальный газ при адиабатическом расширении в вакуум охлаждается. При адиабатическом сжатии в вакуум реальный газ нагревается.