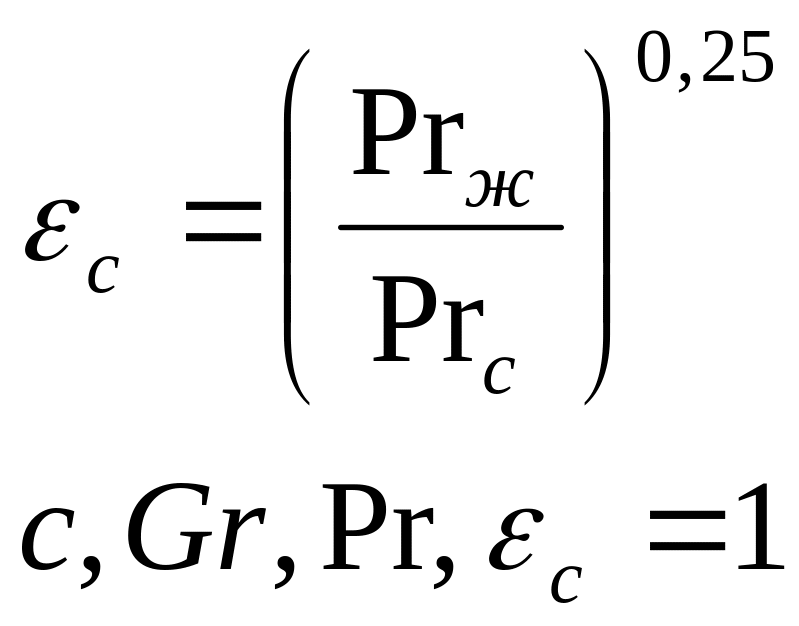Основной закон теплопроводности. Закон Фурье.

Теплопроводность – это физический параметр, характеризует способность вещества проводить теплоту, при этом перенос теплоты происходит через соприкосновение структурных частиц тепла, в разных средах механизм переноса теплоты различен.

В жидкостях и газах обусловлен двойными и тройными взаимодействиями молекул.

В металлах за счет диффузии перемещения свободных электронов.

В твёрдых диэлектриках связан с переносом тепловых колебаний микрочастиц, в виде упругих волн – фононов. В чистом виде теплопроводность проявляется в способах переноса теплоты:

1. Кондукция

2. Конвекция

3. Излучение

В чистом виде кондукция имеет место только в твёрдых телах, в жидкостях и газах она сопровождается конвекцией.

- Кондукция (теплопроводность)

- Конвекция

Закон Фурье

Плотность теплового потока прямопропорциональна градиенту температуры. „ - ” показывает разнонаправленность этих векторов, λ – теплопроводность,

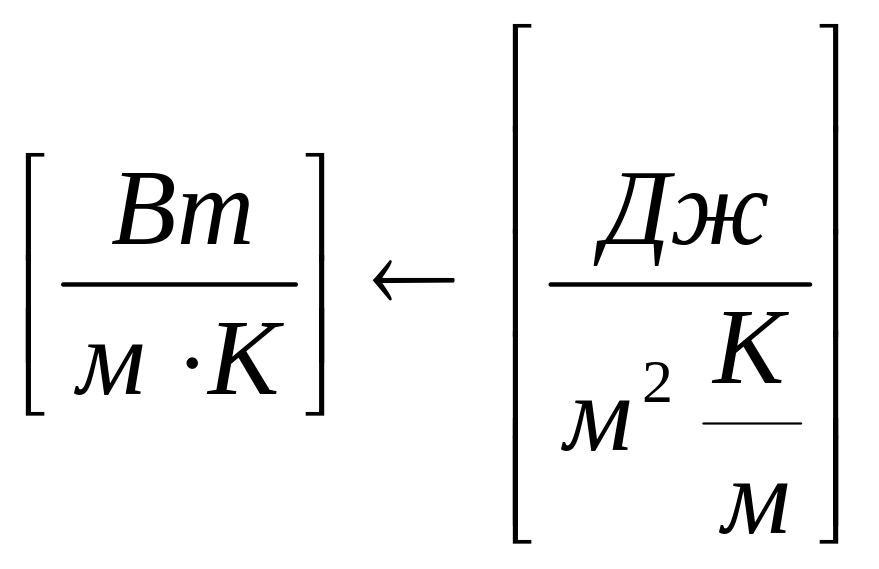
Теплопроводность численно равна количеству теплоты переносимому в единицу времени через единицу площади изотермической поверхности при grad t =1 .Она является физическим параметром и характеризует способность вещества проводить теплоту, зависит от природы и состояния вещества. Определяется опытным путём, находится по таблицам теплофизических свойств индивидуальных веществ.

Лучшими теплопроводниками являются металлы:

- λ= 3-468 (наибольшая для Ag)

Для жидкостей:

- λ= 0,07-0,7

Для больших жидких сред теплопроводность уменьшается с увеличением температуры.

Для газов:

λ= 0,005-0,5

Для воздуха при t = 8˚С , λ= 0,0294 . С увеличением влажности, теплопроводность увеличивается.

, где a-температуропроводность тела,(м²/с). a-это физическая величина, характеризующая скорость изменения температуры в теле и является мерой его теплоинерционных свойств, зависит от природы вещества и его физического состояния. Играет важную роль при нестационарной теплопроводности.

C-теплоёмкость, ρ -плотность. Для определения знака t в любой точке тела необходимо знать частные особенности температурной функции.

где С₁ и С₂ – производные постоянные, которые могут принимать любые значения. Для того, чтобы эта функция была однозначной, необходимую задать частные особенности её существования в конкретной задаче, что конкретизирует значения С₁ и С₂. К ним относится:

1. форма и размеры тела

2. его физические параметры (λ, ρ, C, a)

3. начальное распределение температуры в теле (начальное условие), при .

4. условие теплообмена на границе с внешней средой (граничные условия).

Совокупность начальных и граничных условий называют краевыми условиями.

1. граничные условия 1-го рода - задаётся распределением t на поверхности тела для любого момента времени

2. граничные условия 2-го рода – задаётся поверхностная плотность теплового потока для каждой точки в любой момент времени

3. граничные условия 3-го рода - задаётся температурой окружающей среды и законом теплоотдачи между поверхностью и окружающей средой.

Стационарная теплопроводность.

- плоская однослойная стенка

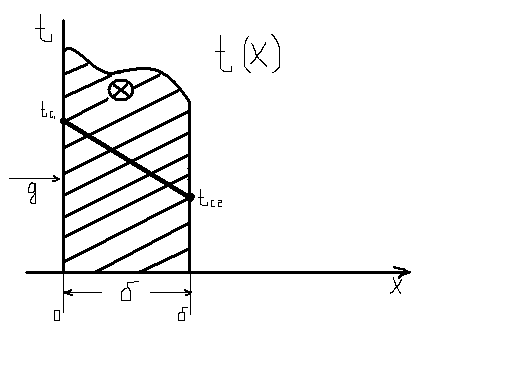
δ -толщина, рассмотрим установившийся режим, т.е. на поверхностях , при этом t_c1 › t_c2.

Теплопроводность λ=const.

Внутренний теплоисточник отсутствует q_v = 0, рассматриваются граничные условия 1-го рода.

1) при x=0 → t = t_c1

2) при x=0 → t = t_c2

Функция распределения теплоты по толщине стенки

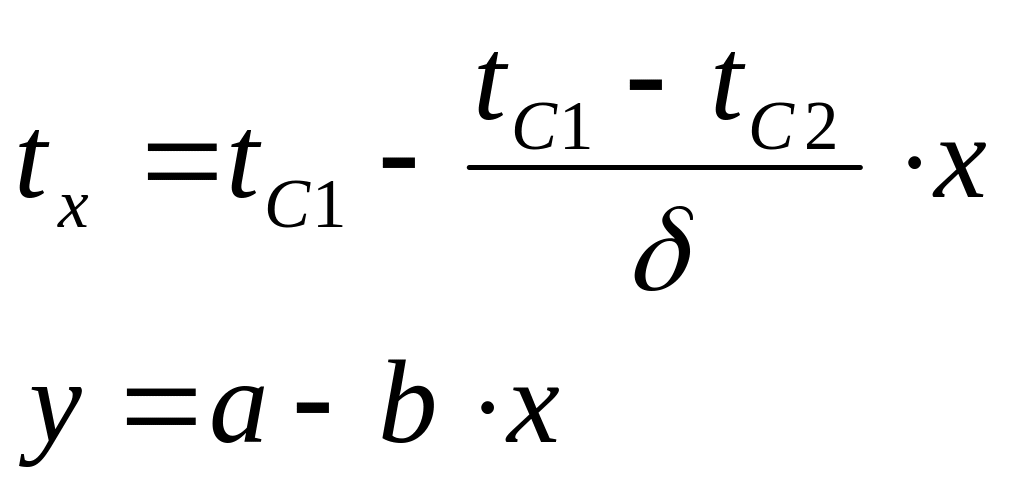
Чем больше угол наклона,

тем меньше теплопроводность стенки λ.

Температура измеряется по линейному закону. Зная температуру можно рассчитать другие характеристики:

1. плотность теплового потока

где R – термическое внутреннее сопротивление теплопроводности стенки.

- многослойная плоская стенка

λ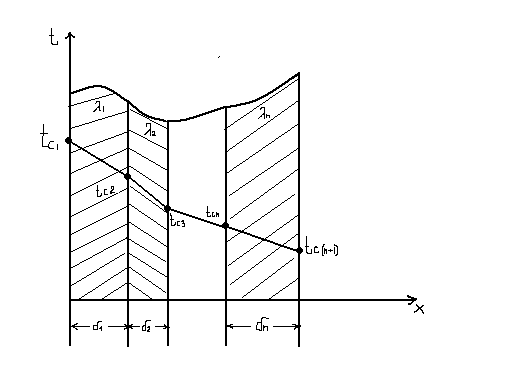 =const, , q_v=0,

1-й слой : q=const

Выражение справедливо для любого слоя (плотность теплового потока)

R_i- термическое сопротивление i-го слоя, К- номер стыка

Измеряется по линейному закону, но наклон их различен. С увеличением сопротивления, уменьшается теплопроводность.

- цилиндрические стенки

r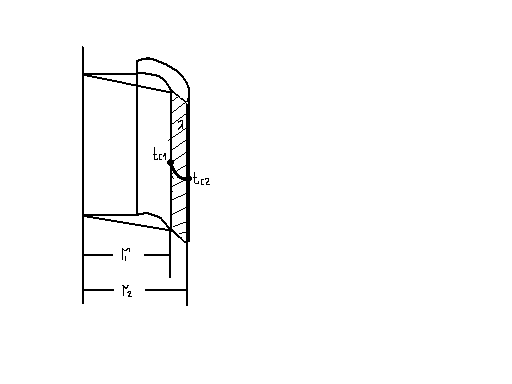 = r₁→ t = t_c1,

r = r₂→ t = t_c2, r →d

Уравнение для текущей температуры

где d – текущий диаметр. При анализах теплопроводности цилиндрических стенок используют линейную плотность теплового потока.

R_λl - линейное термическое сопротивление теплопроводности трубы.

Линейная плотность теплового потока для многослойной цилиндрической стенки.

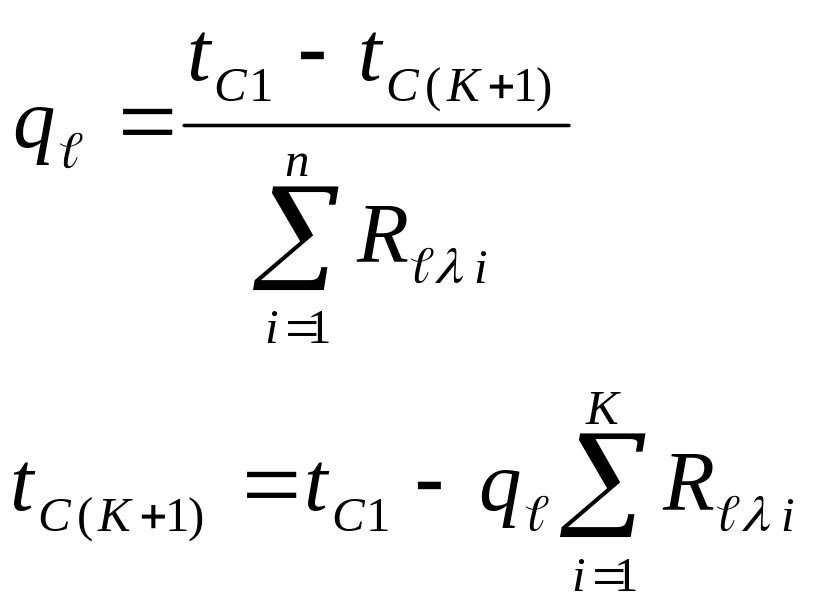
При трубка считается тонкостенной, и расчёт ведут, как для плоской стенки

где d_ср=0,5(d₂+d₁)

Нестационарная теплопроводность.

Одним из методов решения является регулярный режим измерения теплопроводности. Большое разнообразие прикладных задач нестационарной теплопроводности привело к созданию многочисленных методов их решения (нестационарные режимы – пуск оборудования). К ним относятся:

-аналитические

-приближенные

-численные

-аналоговые

-экспериментальные методы

Режим (нагревание) при котором t любой точки тела изменяется во времени экспоненциально называется регулярным режимом.

Средняя по объёму тела избыточная температура

t_v-среднеобъёмная температура тела измеряется во времени, t_ж-постоянная температура среды (жидкость) в которую внезапно вносится тело, при τ =0

тоже самое в начальный момент времени, m, темп охлаждения (нагревания).

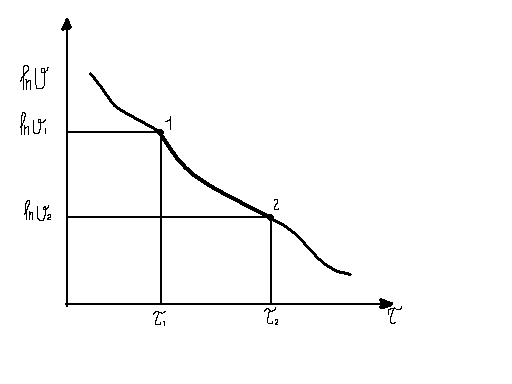
зависит от

- формы и размеров тела

- физические свойства

д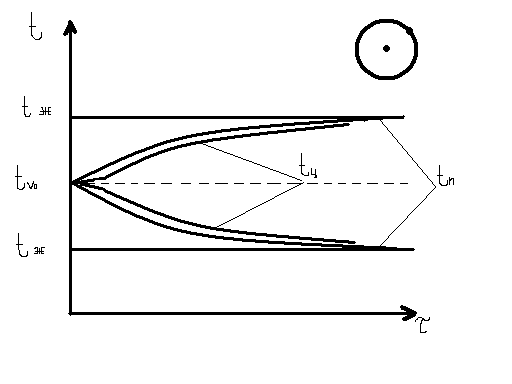 ля шара

для периферийных точек тела (t_п)

для центральных (t_ц)

Понятие о регулярном режиме широко используется для определенного времени нагревания (охлаждения) тела, а также для исследования теплофизических свойств (C, ρ, λ, a, v) вещества, термических сопротивлений.

Теплоотдача. Закон Ньютона - Рихмана.

Теплоотдача- это конвективный теплообмен между жидкостью и поверхностью твердого тела при их непосредственном соприкосновении.

Жидкость- это среда, обладающая свойством текучести, т.е. неограниченное дополнительное изменение формы под действием малых сил.

Конвекция- это способ переноса теплоты в жидкостях и газах.

Различают:

-естественную (свободную)

-вынужденную

Свободная - это перемещение жидкости, вызванное исключительно подъемными силами, возникшее вследствие изменения ρ жидкости и определяется разностью температур жидкости, и поверхности с которой она соприкасается.

Вынужденная - проявляется под действием внешних сил (компрессор, насос, вентилятор). Согласно закону Ньютона – Рихмана, кондуктивный теплообмен предстает уравнением:

берется по модулю, поскольку разность всегда положительная.

α - коэффициент теплоотдачи, характеризует её интенсивность.

Количество теплоты в единицах времени Дж/с = Вт, приходится на единицу площади поверхности 1м², при разности температур в 1К. Коэффициент теплоотдачи есть характеристика процесса, и может быть определён расчетным путем (в отличие от физических параметров C, ρ, которые табулированы).

Величина обратная α 

где R_α- термическое сопротивление теплоотдачи. α = f(ω, t_с, t_ж, C, ρ, λ, v, a)

-форма и размеры

где N_u- число Нуссельта, безразмерный коэффициент теплоотдачи,

l^*- определяющий (характерный) размер,

λ_ж- теплопроводность жидкости, физический параметр, и другие параметры, определяются при характерной (определяющей) температуре, в её качестве может быть рассмотрены: t_ж, t_с, t_ср,=(t_с+t_ж), она зависит от постановки задачи.

l^*- размер, который сильнее всего влияет на интенсивность теплоотдачи:

d_вн, d_н, l, h, d_экв, b_min

Гидродинамический и тепловой пограничные слои.

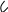
Ламинарный режим- упорядоченный, в x_кр1 наблюдается завихрения, а в x_кр2- турбулентный режим.

δ_п – толщина пограничного слоя (ламинарного)

δ_т – турбулентный слой

δ_лп- толщина ламинарного подслоя

Наличие ламинарного подслоя будет определять коэффициент термического сопротивления теплоотдачи, определяется термическим сопротивлением теплопроводности.

n –толщина пристенного слоя.

Решая эти уравнения совместно, имеем

Аналитическое определение α невозможно.

Теория подобия служит базой для моделирования процессов и аппаратов. Основная цель этой теории - это обобщить зависимости, полученные каким-либо способом на основе отдельных экспериментов, распространить эти результаты на ещё не изученные объекты. В общем случае для подобных систем должно соблюдаться гидродинамическое, геометрическое и тепловое подобие.

b₁ b₂

1) Число Нуссельта- это безразмерный комплекс, число подобия. Теория подобия рассматривает подобные явления

2) Числа гидродинамического подобия

-число Фруда

характеризует соотношение сил тяжести и сил инерции при вынужденном движении жидкости.

- число Грасгофа

β- температурный коэффициент объёмного расширения

g=9,8;

∆t- температура |t_с- t_ж|;

υ- кинематическая вязкость;

l*- определенный размер;

t^*- определенная температура, по ней определяется физические параметры, входящие в числа подобия (λ, υ, ρ, a), характеризует соотношение между подъёмной силой возникающей в среде, следует разности плотностей и силами молекулярного трения.

- число Рейнольдса

безразмерная скорость, режимный фактор, характерное соотношение между силами инерции и вязкости, который определяет гидродинамический режим вынужденного течения жидкости.

- число Эйлера

∆P- гидравл. сопротивление. Служит мерой соотношений перепада статических давлений в потоке (гидравл. сопротивления) к кинетической энергии потока.

3)Числа теплового подобия

– число Фурье

τ- безразмерное время. Характеризует связь между скоростью изменения температурного поля физическими параметрами и размерами тела

- число Био

λ_ст- теплопроводность стенки. Устанавливает соотношение между теплоотдачи с поверхности тела и подвода теплоты из внутренних слоев тела к поверхности кондукцией.

- число Пекле

характеризует соотношение между переносом теплоты конвекций и кондукцией в потоке.

- число Прандтля

характеризует влияние физических свойств жидкости (υ, a), является мерой подобия полей температур и скоростей.

- число Рэлея

- число Нуссельта

характеризует интенсивность теплоотдачи - безразмерный коэффициент теплоотдачи.

Критериальное уравнение теплоотдачи Nu = f(Fa, Re, Gr, Pr)- нестационарный теплообмен.

Примечание: различные определяемые и определяющие числа – они содержат все известные числа, определяемые – неизвестные.

Nu = f (Re, Gr, Pr) - стационарный теплообмен

Nu = f (Re, Pr) - вынужденное

Nu = f (Gr, Pr) - свободное

Теоремы подобия:

1. Подобные между собой явления имеют одинаковые числа подобия – т. Бертрана

2. Исходные математические уравнения характеризующие данное физическое явление всегда могут быть представлены в виде зависимости между числами подобия (уравнения подобия), характеризует это явление – т.Букингема

3. Подобны те явления, условия, однозначности которых подобны и для которых числа подобия состоят из условия однозначности численно равны – т. Кирпичева - Гухмана.

Критериальное уравнение в виде степенной функции.

Nu_жd- среднее значение, ж- температура жидкости опред-я, d- опред-ий размер- диаметр,

c, m, n, k- коэффициент и показатели степени

Nu	C	Rℓm	Grn	Prk	εc	εℓ	εn	Примечание
1)свободная конвекция	+	-	+	+	+	-	-
2)вынужд. движ. жидкости вдоль пл.ст.	+	+	-	+	+	-	-	CRem для возд.
3)движение жидкости в трубе а)ламинарн.	+	+	+	+	+	+	-	CRemGrn для возд.
б) турбулентн.	+	+	-	+	+	+	-

C, m, n, k- зависят от

-режима течения жидкости (ламинарный, турбулентный, переходной)

-физические свойства жидкости

-от характера обтекания поверхности (продольное, поперечное)

-состава поверхности (одиночная труба, пучок труб)

-условия теплообмена (при свободной, при вынужденной конвекции)

-агрегатное состояние (постоянство или изменение)

Ε-поправки, Е_с- поправки, учитывающие влияние направления теплового потока на теплоотдачу.

Если средой является газ, то Е_с=1. Для воздуха CRe^m

Е_l- поправка, учитывающая влияние начального участка стабилизации

Е_l=1

1, Е_l=1,9

5 Е_l=1,44

10 Е_l=1,28

20 Е_l=1,13

30 Е_l=1,05

40 Е_l=1,02

Для длинных труб , ε_ℓ = 1. В конце начального участка наступает стабилизация темп.поля

ламинарное турбулентное

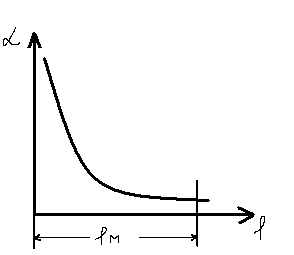
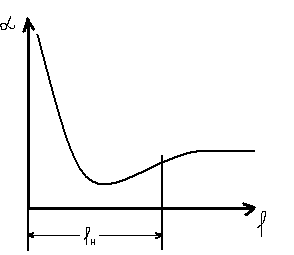
1. l_н^турб< l_н^лам

2. α_стаб^турб>α_стаб^лам (стаб- стабилизированный)

3. α_{на нач. уч-ке}>α_стб

При свободной конвекции

Т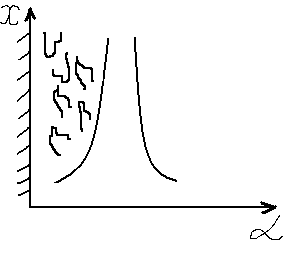 урбулизация

Теплоотдача при поперечном обтекании труб и трубных пучков. Nu= CRe^mGrⁿPr^kE_cE_lE_n - среднее значение, ж-опр.температура жидкости, d-опр.размер-диаметр

, с-температура стенки

, ж-температура жидкости

Nu=	c Rem Grn Prk Ec El En	Примечание
Одиночная труба	+ + - + + - -	Для возд. cRem
Пучок труб	+ + - + + - +	Для возд. cRemEn

Обтекание одиночной трубы

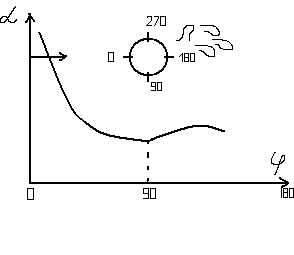
min толщина слоя Турбулизация

при Re = 10-10³, с = 0,5;

m = 0,5; k = 0,38

при Re = 10³- 2*10⁵, с = 0,25;

m = 0,6; k = 0,38

для возд. с = 0,43;

m = 0,5

для возд. с = 0,216;

m = 0,53

Срыв потока

Пучок труб

Е_п = Е_iЕ_ψЕ_s, Е_i - множитель, учитывающий N ряда труб в пучках, Е₁=0,6; Е_2(шахм)=0,4; Е_{2(корид)}=0,9; Е₃=1

Продольный Поперечный

S₂ S₂



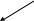
S _{1 60} S₁

^dн ₃₀

₀ происх.турбулиз.

К оридорный пучок Шахматный пучок

Интенсивность Интенсивность

С 3-го ряда установившийся теплообмен, Е₄-коэффициент, учитывающий влияние угла атаки потока на пучок

-если < атаки 0, Е₄=1

30^°, Е₄=0,95

60^°, Е₄=0,67

80^°, Е₄=0,55

Е_s- влияние относительных поперечного и продольного шагов.

относительный шаг

Для шахматного пучка при S₁/S₂<2, Е_s= (S₁/S₂)^1/6

S₁/S₂≥2, Е_s=1,12

Для коридорного пучка Е_s= (S₂/d_н)^0,15

Для коридорных пучков c=0,26; m=0,65; k=0,33

Для шахматных пучков c=0,41; m=0,6; k=0,33

Турбулизация потока в шахматном пучке выше, чем в коридорном, и теплоотдача при прочих равных условиях выше.

Теплоотдача при кипении и конденсации выше, чем в однофазной жидкости, за счет фазового перехода.

Теплоотдача при кипении

∆ t- степень перегрева жидкости стенки относительно t_н

режимы кипения в большом объёме:

1) Исп. при активной конвекции а;

2)Пузырьковый режим кипячения b, пленочное

кипение.

Плотность теплового потока достигает своего max значения. называемого критическим q_кр1,

r- удельная теплота парообразования,

σ-коэффициент поверхностного натяжения жидкости,

ρ- плотность

Для воды при атмосферном давлении

∆t_кр=23-27^°С

α_кр=46,5*10³ Вт/м²К

q_кр= 1,16*10⁶ Вт/м²

Лобунцов предложил Критериальное уравнение теплоотдачи:

σ- коэффициент повышения натяжения

α=3,0q^0,7p^0,15

α= 38,7∆t^2,33p^0,5

q- плотность теплового потока

p- давление в барах

∆t- разность температур

Теплоотдача при конденсации

t_с < t_н

В зависимости от состояния поверхности, природы жидкости конденсация может быть

- пленочная

- капельная

кондуктивный перенос

конвективный

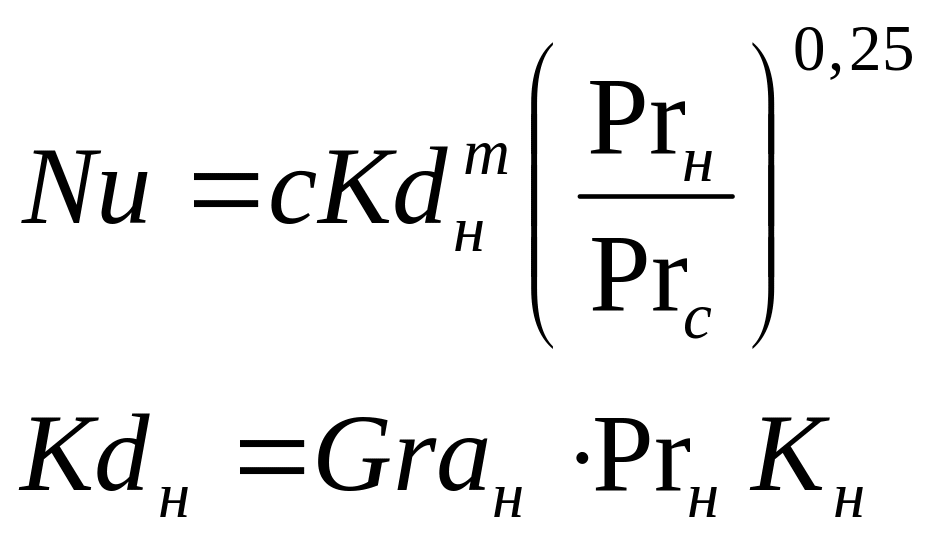
Кd- критерий конденсации,

Grа_н - критерий Галилея Grа_н = q(l^*)²/ υ_н²

К_н - критерий Кутателадзе К_н = r/(с_p∆t_н)

Определенный размер- высота или диаметр горизонтальной трубы

Коэффициент с для вертикальных труб и стенок 0,42, для горизонтальных 0,72

m_в=0,28; m_г=0,25.

Эмпирические формулы для определения среднего коэффициента теплоотдачи.

с=0,943-вертикальная труба, d опр.

с=0,728-горизонтальная труба, d опр.

l^*→d

Излучение, лучистый теплообмен.

Природа корпускулярно- волновая и состоит в испускании телом в окружающую среду электромагнитных колебаний. Отсутствует непосредственное соприкосновение между телами – главная особенность. Излучение осуществляется прямолинейно, со скоростью света, по всем направлениям и подчиняется закону геометрической оптики. При встрече потока частиц с препятствием, электромагнитные колебания преобразуются во внутреннюю энергию, что сопровождается нагреванием тела. Для любого тела можно записать баланс лучистой энергии:

Q_А+ Q_R+ Q_Д= Q : Q, А+R+Д=1

Q_R Q

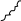
А - поглощательная способность

R - отражательная

Д - пропускательная

Q_Д

А = 1, R = 0, Д = 0-абсолютно черное тело (сажа), Е = 1- степень черноты

R = 1, А = 0, Д = 0- абсолютно белое тело (полированный металл)

Д = 1, А = 0, R = 0- абсолютно прозрачное тело (двухатомные газы О₂, N₂, H₂)

Основные законы теплового излучения.

закон Планка

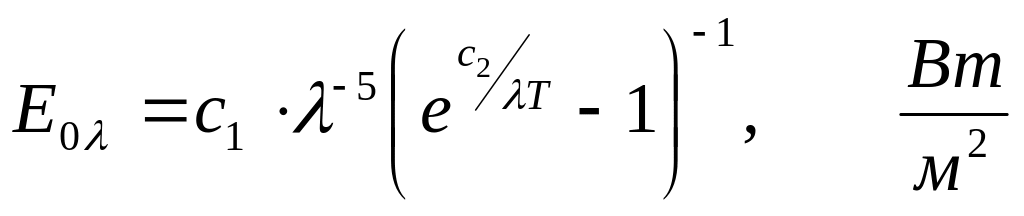
Плотность потока излучения при данном значении длины волны (спектральная плотность потока излучения) для абсолютно черного тела.

λ- длина волны

Т - абсолютная температура тела, К

с₁=3,68*10^-16, Вт/м²

с₂=1,44*10^-2, Вт/мК

е-экспонента

закон смещения Вина λ_maxТ=2,89*10^-3,мК

Отражает смещение максимума спектральной плотности с увеличением температуры в сторону коротких длин волн.

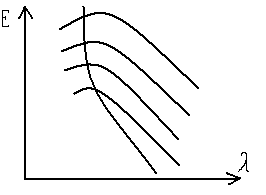
С увеличением Т,

2000˚ С max смещается в сторону

1500˚ С коротких волн.

1000˚ С С увеличением Т,

энергия излучения

500˚ С повышается.

Е = 0

Закон Стефана- Больцмана

Поверхностная плотность потока излучения (лучистый поток с единичной поверхности тела) по всем направлениям в пределах телесного полусферического угла, пропорциональна абсолютной температуре в 4-й степени

С₀ = 5,7 Вт/(м²К)⁴- коэффициент излучения абсолютно черного тела

Е = ε∙Е₀, ε-степень черноты

Кривая распределения спектральной плотности потока излучения

Е_λ=f (λ)

Для серого тела лежит несколько ниже, чем для аналогичной кривой для черного абсолютного тела при той же температуре.

Абсолютно серое тело

Абсолютно черное тело

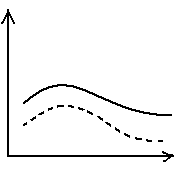
Е_λ

λ

Особенности к излучению газов

Опыт показывает, что излучение газов отклоняется от закона абсолютной температуры в 4-й степени. Оставляя в силе закон Стефана- Больцмана, с введением корректирующего множителя.

ε_г- степень черноты объема газа, ε_г=f(t,P_i*l),

P_i*l- произведение парциального давления на длину пути луча в объеме газов

закон Кирхгофа

Отношение энергии излучения к энергии поглощения для любого тела одинаково и равно энергии излучения абсолютно черного тела при той же температуре. Квантовый механизм преобразования энергии в теле в процессе её излучения и поглощения одинаков.

Степень черноты тела равна его поглощательной способности.

закон Ламберта

Е = Е_n = Е_max

В направлении нормали к излученной поверхности, излучение максимально, а в направлении <φ к нормали излучение составит

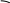Е = Е_ncos φ 

Лучистый теплообмен между телами

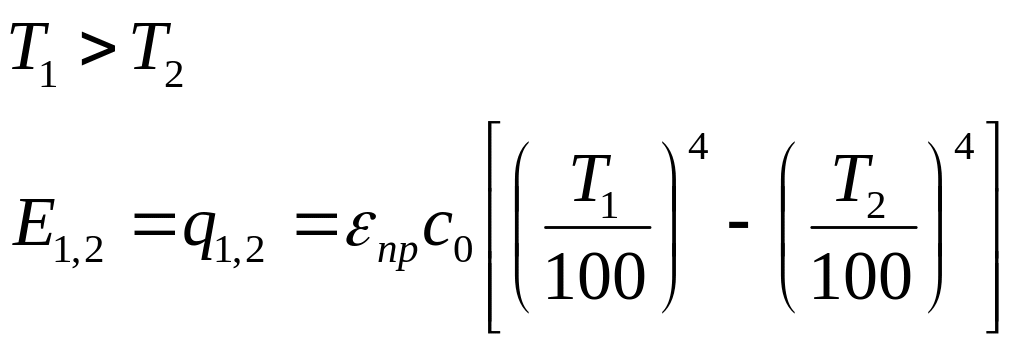
- приведенная степень черноты двух тел.

При установке экрана приведенная степень черноты выражается зависимостью.

Установка экрана между поверхностями уменьшает лучистый тепловой поток в 30-40 раз

ε_сэф = 0,5 (ε_с+1) - эффективная степень черноты тепловоспринимающей стенки.

ε_с-степень черноты материала

ε_г-степень черноты объема газа

радиационный теплообмен ( конвекция и излучение)

Теплопередача (сложный теплообмен):

1. кондуктивный,

2. излучение,

3. конвективный.

Многослойная плоская стенка

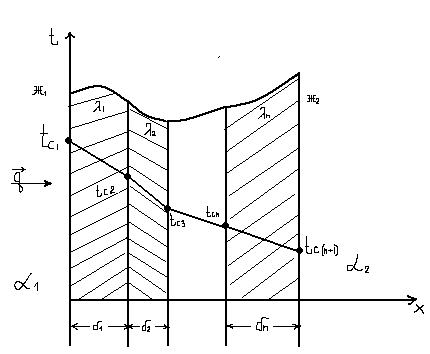
если заданы з. переноса теплоты между жидкостью и стенкой, то заданы гранитные условия 3-го рода

Наклон линий изменения температуры зависит от λ, чем выше λ, тем более пологая линия

q = const - уст-ся режим

q_υ = 0

закон Ньютона - Рихмана

q = α₁(t_ж1-t_с1) =

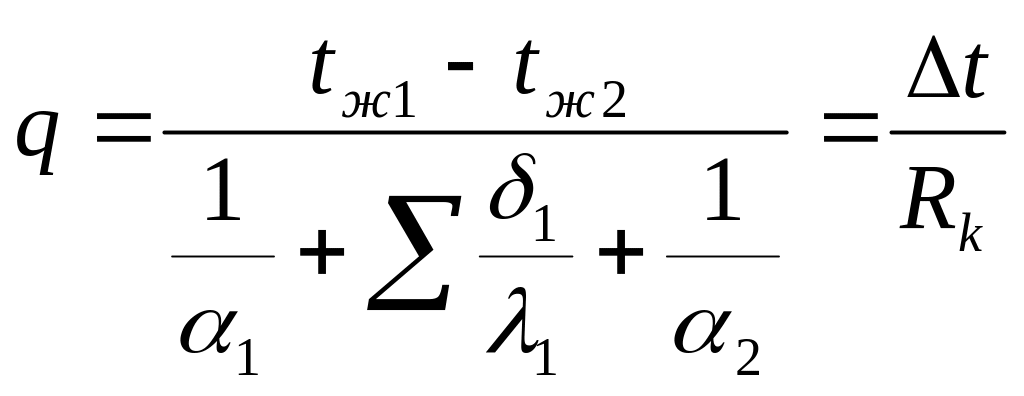
- термическое сопротивление теплопередачи

Rα-термическое сопротивление теплоотдачи

Величина, обратная R_к называется коэффициентом теплопередачи, характеризует интенсивность теплопередачи от горячего теплоносителя к холодному, через разд.поверхность.

линейное термическое сопротивление.

- линейная плотность теплового потока

Способы регулирования интенсивности теплопередачи.

1. создание развитых поверхностей теплообмене за счёт их оребрения, со стороны меньше α;

2. искусственная турбулизация потока;

3. оптимизация поверхностей теплообмена.

В зависимости от конечной цели расчета различают

1) конструктивный;

2) проверочный расчеты.

По роду носителя:

- водоводяной;

- пароводяной.

По компоновке:

- труба в трубе

По технологии сборки:

- секунонные

В основе расчетов лежит решение уравнений теплопередачи и теплового баланса

q=К∆t, Вт/м²

Q=КF∆t, Вт

К -коэффициент теплопередачи, ∆t-средний температурный напор

Процесс теплообмена протекает при постоянном давлении.

Теплота в изобарном процессе определяется как разность энтальпий.

Для оценки эф. теплообмена привлекают КПД

- эксергетический баланс

П - эксергетическая потеря:

→ вода, п.пар табл.

- энтальпия конденсата

С_р = 4,19