Литература:

1) Теплотехника под редакцией Баскакова – 1982, 1991

2) Техническая термодинамика и теплопередача – Нащекин

Термодинамика.

Изучает закономерности превращения одних видов энергии в другие. Энергия – это количественная мера движения материи.

1) Различают: внутреннюю энергию и энергию в переходе термодинамической системы из одного состояния в другое. Термодинамическая система – это совокупность материальных тел, находящихся в механической и тепловой взаимосвязи между собой. Тела не входящие в нее образуют окружающую среду. Между системой и окружающей средой существует контрольная поверхность, оболочка. Хаотическое движение, внутримолекулярное движение связаны с внутренней энергией.

Энергию в переходе можно рассматривать как формы переноса энергии: теплота и работа. Способы переноса теплоты: кондукция, конвекция и излучение. Виды работы: механическая, электрическая, магнитная.

О различиях в теплоте и работе судим по принципу превратимости: работа может быть полностью превращена в тепло, но, теплота не может полностью превратиться в работу. Перенос энергии в форме теплоты связан с хаотическим движением частиц, работа же связана с упорядоченным движением.

• - Работа L, Дж

• - Удельная работа l,

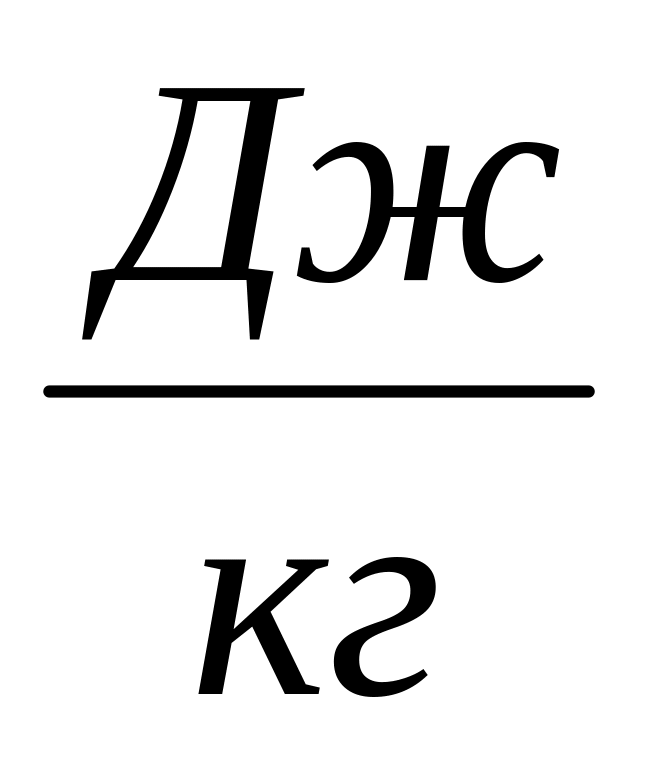
• - Теплота Q, Дж

• 1Дж (L) = 1Дж (Q) они разные по качеству

• - Удельная теплота q,

	Подвод	Отвод
L	−	+
Q	+	−

Открытой называется термодинамическая система, которая может обмениваться с окружающей средой веществом. Если вещество не проходит через границы системы, то она называется закрытой.

2) Основные термические параметры состояний.

• - абсолютное давление, ;

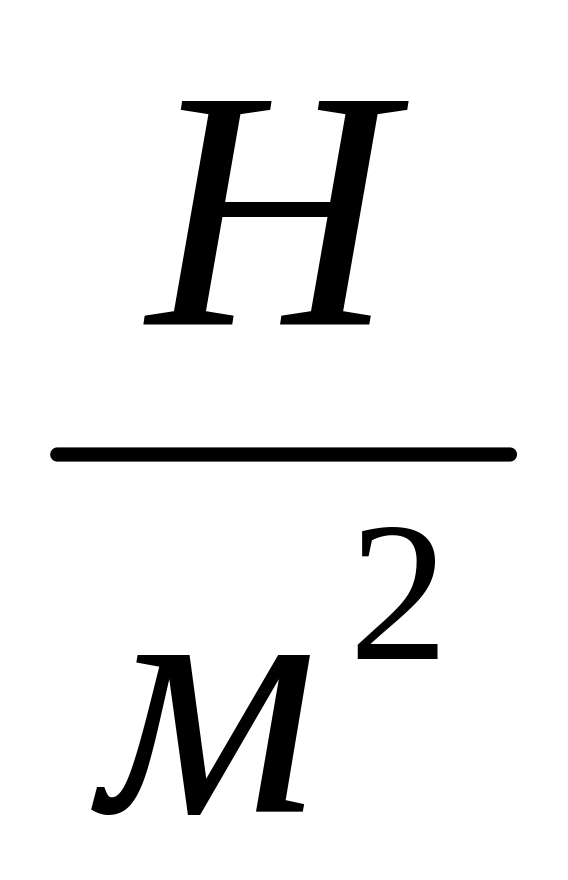
• - абсолютная температура;

• - удельный объем.

10³ Па = 1кПа

10⁶ Па = 1МПа

10⁵ Па = 1 бар

ат

мм. рт. ст.

м. вод. ст.

Теплоизолированной (адиабатной) называется термодинамическая система, которая не может обмениваться теплотой с окружающей средой.

Система, не обменивающаяся с окружающей средой ни энергией, ни веществом называется изолированной.

Давление обусловлено взаимодействием молекул рабочего тела с поверхностью.

Температурой называется физическая величина, характеризующая степень нагретости тела.

, то _(манн)

, то _(разр)

Абсолютная температура

Т, К

0 К – всякое движение отсутствует

273,16 К – соответствует состоянию характерного для тройной точки, лед + вода + пар, находящейся в термодинамическом равновесии.

1 К =

t, C˚

0˚ C – таянье льда

100˚ С – кипение воды при нормальном

1˚ С = , t_тр = 0,01˚ С, Р_тр = 611 Па

Т – 273,16 = t – 0,01

Т = 273,15 + t ∆T = ∆t

Фаренгейт

t =

Ренкин 1R =

Удельный объем:

удельный объем – это объем единицы массы вещества.

Нормальные условия

Р = 760 мм. рт. ст. = 101,325 кПа

Нормальные физические условия

t = 0˚ С = 273 К

Р = 735,6 мм.рт.ст = 98,1 кПа

Нормальные технические условия

t = 15˚ С = 288 К

Идеальным называется газ, в котором отсутствуют силы взаимодействия между молекулами, размер самих частиц бесконечно мал по сравнению с расстоянием между ними.

К идеальным газам относят: атмосферный воздух (водяной пар), продукты сгорания органического топлива. Водяной пар полученный из Н₂О в результате подвода к ней Q – есть реальный газ.

Уравнение Клапейрона.

- газовая постоянная – это есть работа, которую надо совершить над 1 кг газа в изобарном процессе с тем, чтобы его температура изменилась на 1К.

Уравнение Менделеева – Клапейрона.

универсальная газовая постоянная.

Для реального газа данное уравнение справедливо, для них используется уравнение Ван-дер-Ваальса:

a и b – на практике используют таблицы и диаграммы.