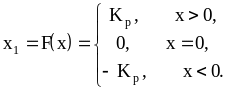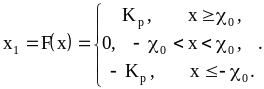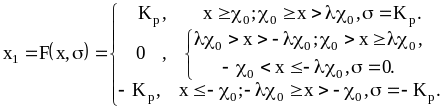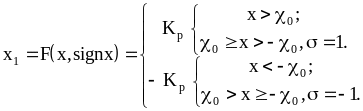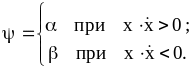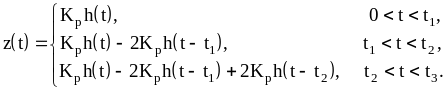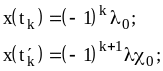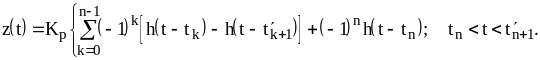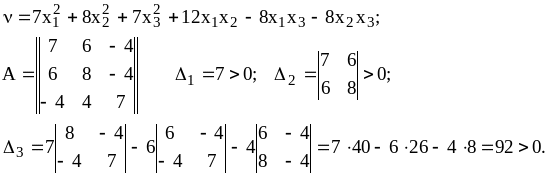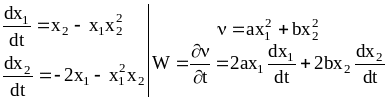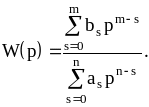7.2 Оценка качества сау по расположению корней характеристического уравнения

Рассмотрим характеристическое уравнение САУ:

. (7.6)

Если при имеем , то ему соответствует составляющая переходного процесса:

, (7.7)

если есть пара комплексно-сопряженных корней , то для них

. (7.8)

Как видно из выражений (7.7) и (7.8), интенсивность затухания переходного процесса определяется величиной отрицательной вещественной части корня. Потребуем, чтобы все составляющие переходного процесса за время уменьшилась не менее чем в раз. Тогда

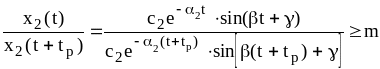. (7.9)

Поскольку огибающей составляющей переходного процесса является экспонента, за которую кривая не выходит, то, предположив, что точки и находятся на ней, получим:

. (7.10)

откуда . (7.11)

Условие (7.11) указывает на то, что если по модулю отрицательная часть всех корней характеристического уравнения (7.6) будет не менее , т.е. все корни будут располагаться левее прямой, проведенной на комплексной плоскости параллельно оси ординат на расстоянии слева, то каждая составляющая переходного процесса уменьшается за время не менее чем в раз (рисунок 7.1).

Это условие можно определить не решая характеристическое уравнение. И.Н.Вознесенский впервые использовал для этой цели критерий Гурвица (1941 г.) и связал его с длительностью переходного процесса.

Для того чтобы все корни характеристического уравнения (7.6) находились левее прямой , проведенной на расстоянии, обеспечивающим требуемую абсолютную степень затухания, необходимо, чтобы преобразованное характеристическое уравнение заменой удовлетворяло условию устойчивости. Для рисунка 7.1 справедливы соотношения: .

Заменив в (7.6) на , получим:

. (7.12)

Применяя к (7.12) критерий Гурвица, определяем выполнение условия требуемой абсолютной степени затухания. Рассматриваемое условие может быть проверено с помощью критерия Михайлова.

Для того чтобы вектор скользил по линии , обеспечивая поворот против часовой стрелки при изменении от до , необходимо в характеристическом уравнении

(7.13)

выбрать соответствующим образом . Из рисунка 7.1 видно:

; , т.е. .

Подставляя в выражение (7.6) вместо , получаем . (7.14)

Если , то САУ обладает требуемой абсолютной степенью затухания.

Иногда требуется уменьшение амплитуды гармонических колебаний каждой составляющей переходного процесса за период в раз. В этом случае

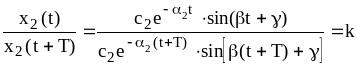, (7.15)

или , где , поэтому . (7.16)

Для выполнения указанного условия необходимо, чтобы все корни характеристического уравнения располагались в секторе, ограниченном лучами, проведенными под углом к мнимой оси (рисунок 7.2).

Проверка этого условия может быть произведена с помощью критерия Михайлова. В данном случае вектор должен скользить по лучам и при изменении от до .

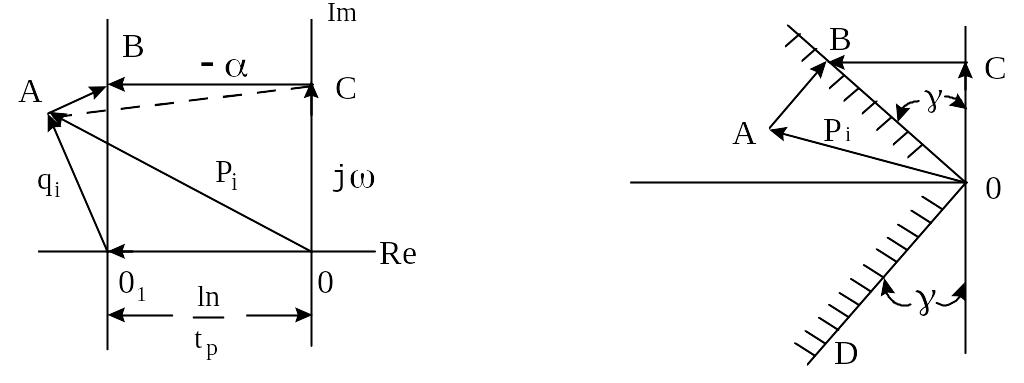
Рисунок 7.1 - Оценка абсолютной Рисунок 7.2 - Оценка относительной

степени затухания степени затухания

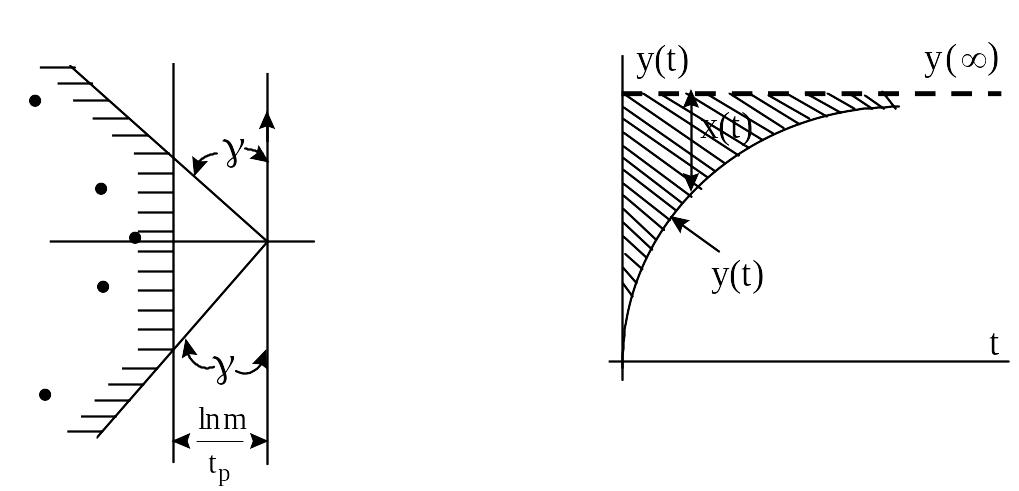
Рисунок 7.3 - Область требуемой абсолют- Рисунок 7.4 - Интегральная

ной и относительной степени затухания оценка качества САУ

Рисунок 7.5 - Вид колебательных процессов

Из рисунка 7.2 , откуда

; .

Подставляя найденное значение в выражения (7.6) и (7.13), получим годограф

. (7.17) При изменении от до каждый из составляющих векторов повернется на угол , если он находится вне сектора .

Если все корни характеристического уравнения (7.6) находятся внутри сектора, ограниченного углами , то выполняется условие относительной степени затухания и

.

Учитывая, что вещественная часть - четная функция, можно изменять от до , при этом

. (7.18)

Можно потребовать чтобы САУ одновременно удовлетворяла условию абсолютной и относительной степени затухания. В этом случае корни характеристического уравнения должны находиться в области, ограниченной двумя лучами проведенными под углом к мнимой оси, проведенной слева от нее на расстоянии (рисунок 7.3).

7.3 Интегральные оценки качества САУ

Наиболее простым интегральным критерием качества САУ является критерий учитывающий интеграл отклонений регулируемой величины.

, (7.19)

где . Здесь - регулируемая величина, - установившееся значение регулируемой величины (рисунок 7.4). Этим критерием можно пользоваться только в случае знакопостоянства . САУ тем лучше, чем меньше , т.е. чем меньше площадь, ограниченная кривой и прямой (рисунок 7.4). В пределе она может быть равна нулю, когда выходная величина устанавливается мгновенно на новом заданном значении.

Вычислить интеграл (7.19) можно двумя способами. В первом способе учитывается то, что является фактически свободной составляющей процесса, поскольку отсчитывается от нового установившегося состояния. Если имелось исходное дифференциальное уравнение

,

то сделав замену , мы получим однородное дифференциальное уравнение

. (7.20)

Выражение (7.19) с учетом уравнения (7.20) можно записать так :

.

Так как , то

.

Поскольку при имеем новое установившееся состояние, от которого производим отсчет, то

и

. (7.21)

Начальные условия определяются из исходного уравнения с учетом правой части.

Второй метод вычисления предложил в 1940 академик В.С. Кулебакин.

Пусть САУ имеет передаточную функцию

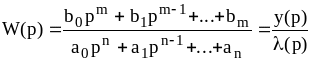и (7.22)

Тогда .

Поскольку , то, устремив к нулю, получим

.

По теореме о конечном значении оригинала функции

.

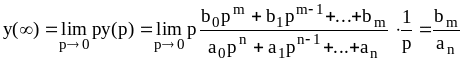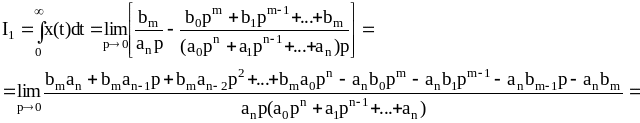
С учетом полученного результата получим формулу (7.23):

(7.23)

Этой формулой можно пользоваться при нулевых предначальных условиях, в то время как на выражение (7.21) это условие не распространяется.

Интегральный квадратичный критерий качества

(7.24)

Идея его использования принадлежит Л. Н. Мандельштаму и Н. Д. Папалекси (1907-1910 гг.). Оценка качества САУ по может производиться для случая колебательных систем (рисунок 7.5). Однако частота колебаний при этом не учитывается. Параметры САУ стремятся выбрать так, чтобы квадратичная оценка приняла минимальное значение. Для этой цели выражают через эти параметры и затем ищут их значения, минимизирующие значения из уравнений:

; , ,

где , , - варьируемые параметры.

Лишен недостатка, присущего , улучшенный квадратичный критерий качества:

, (7.25)

где - некоторая постоянная времени, учитывающая долю влияния скорости изменения регулируемой величины на .

При получаем обычный квадратичный критерий качества.

Оптимальный вид переходного процесса для представляет скачок, как и возмущение . Для улучшенного квадратичного критерия, как доказал А.А. Красовский, оптимальным является переходный процесс, изменяющийся по экспоненте с постоянной времени, равной :

.(7.26)

Из выражения (7.26) следует, что достигает максимума,

если . Это возможно в том случае, когда , или .

Для конкретной системы это условие может оказаться недостижимым, когда . В выражение для входят параметры регулятора, поэтому выбирают их из условия минимума , как в предыдущем случае.

7.4 Оценка качества САУ по частотным характеристикам

Рассматривая запас устойчивости САУ по модулю и фазе, было установлено, что они определяются расположением на комплексной плоскости АФХ разомкнутой системы. Для обеспечения соответствующих параметров (запаса устойчивости по модулю и фазе) необходимо, чтобы АФХ разомкнутой САУ не заходила в определенную зону на комплексной плоскости (рисунок 7.6).

Широкое распространение для анализа качества главным образом следящих систем (с единичной обратной связью) получил так называемый показатель колебательности. Некоторые зарубежные авторы под показателем колебательности понимают величину максимального значения АФХ замкнутой системы по задающему воздействию , отечественные ученые В.А.Бесекерский, А.А.Красовский, В.В.Солодовников принимают за отношение к ее начальной ординате при :

. (7.27)

В общем любую систему управления можно рассматривать как САУ с единичной обратной связью, если измеритель отнести к объекту. Тогда, обозначив АФХ разомкнутой САУ через , АФХ замкнутой системы по заданию запишем в следующем виде:

. (7.28)

Для астатической системы и понятия для совпадают. Для статической системы эти понятия будут тем ближе, чем больше коэффициент усиления разомкнутой САУ :

. (7.29)

Недостатком задания запаса устойчивости по модулю и фазе является необходимость знания двух чисел и . Анализ САУ по показателю колебательности требует знания одного числа .

Чем меньше запас устойчивости, тем больше склонность САУ к колебаниям, тем выше резонансный пик на . Допустимое значение показателя колебательности определяется на основе опыта эксплуатации САУ. Считается, что в хорошо демпфированной системе .

Для отыскания показателя колебательности нет необходимости строить АФХ замкнутой САУ. Можно его определить по АФХ разомкнутой системы, если на комплексной плоскости нанести окружности с известным показателем колебательности.

По определению

.

.

.

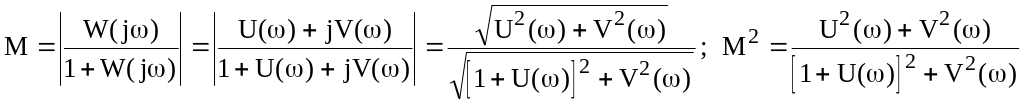Разделим все слагаемые на :

.

Обозначим , тогда .

Прибавим и вычтем в левой части уравнения.

Тогда ;

Обозначим ; .

С учетом обозначений исходное уравнение можно записать так:

. (7.30)

Это есть уравнение окружности радиусом и с центром, смещенным влево от начала координат на величину , рисунок 7.7. Если обозначить через - расстояние от начала координат до окружности с заданным значением , то

.

При окружность вырождается в прямую, параллельную мнимой оси, смещенную влево от нее на расстояние .

При окружность вырождается в точку с координатами .

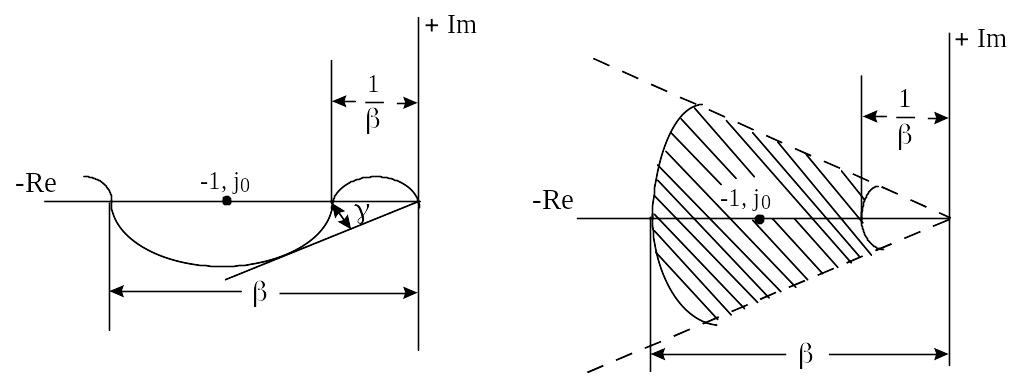
Рисунок 7.6 - Запретная зона для АФХ разомкнутой САУ

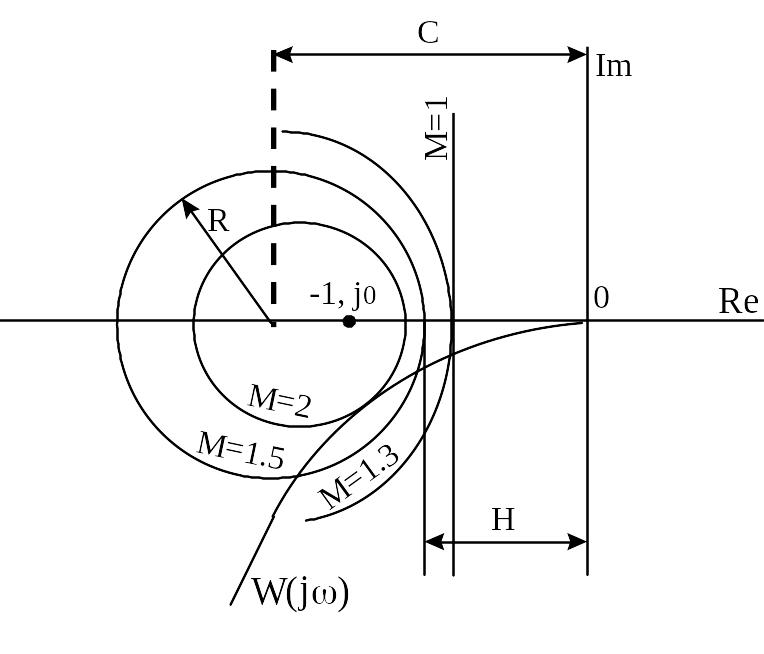
Рисунок 7.7 - САУ обладает требуемым показателем

Нанеся в тех же координатах АФХ разомкнутой САУ, мы найдем значение для минимальной окружности, касающейся АФХ и характеризующей колебательность замкнутой системы.

Очевидно, что запас устойчивости САУ по фазе будет определяться так: , откуда . (7.31)

Быстродействие САУ может быть определено по частоте среза. Если переходный процесс заканчивается за колебания, то .

Время достижения первого максимума или ,

где - частота, соответствующая точке АФХ, ближе всего расположенной к точке на комплексной плоскости .

8 УЛУЧШЕНИЕ КАЧЕСТВА САУ

8.1 Введение производной в закон регулирования

Рассмотрим систему, изображенную на рисунке 8.1. Здесь пунктиром показано корректирующее звено с передаточной функцией .

Передаточная функция разомкнутой нескорректированной САУ . При анализе устойчивости САУ по критерию Найквиста - Михайлова строится АФХ разомкнутой системы . После введения корректирующего звена результирующая передаточная функция разомкнутой системы будет . При этом ее АФХ также изменится. Обозначим ее :

. (8.1)

Из выражения (8.1) видно, что наличие производной приводит к деформации исходной АФХ за счет добавления к каждому вектору дополнительного вектора , направленного перпендикулярно исходному в положительном направлении, рисунок 8.2. (против хода часовой стрелки).

На рисунке 8.2 деформированная АФХ пересекает отрицательную вещественную ось правее исходной, т.е. введение производной может увеличить запас устойчивости по модулю. Однако это не всегда так. В зависимости от формы и выбора величины наличие производной может как повысить, так и понизить запас устойчивости по модулю (удалить или приблизить АФХ к критической точке на комплексной плоскости ).

Введение производной повышает быстродействие САУ.

Действительно, пусть . Тогда, подобрав ,

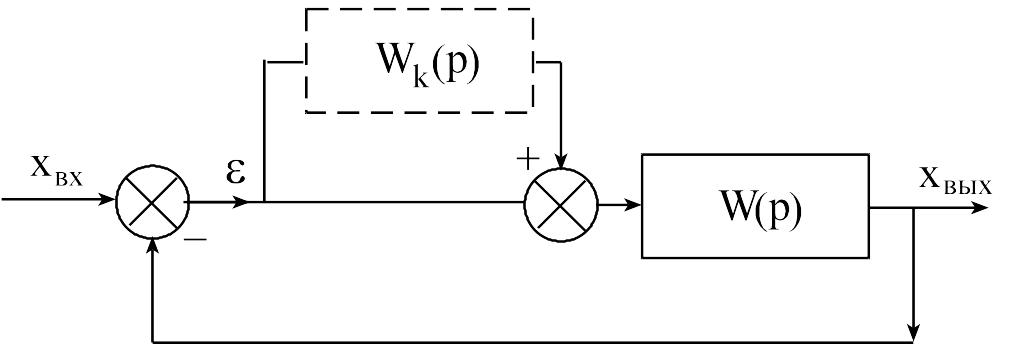
Рисунок 8.1 - Структурная схема инвариантной САУ

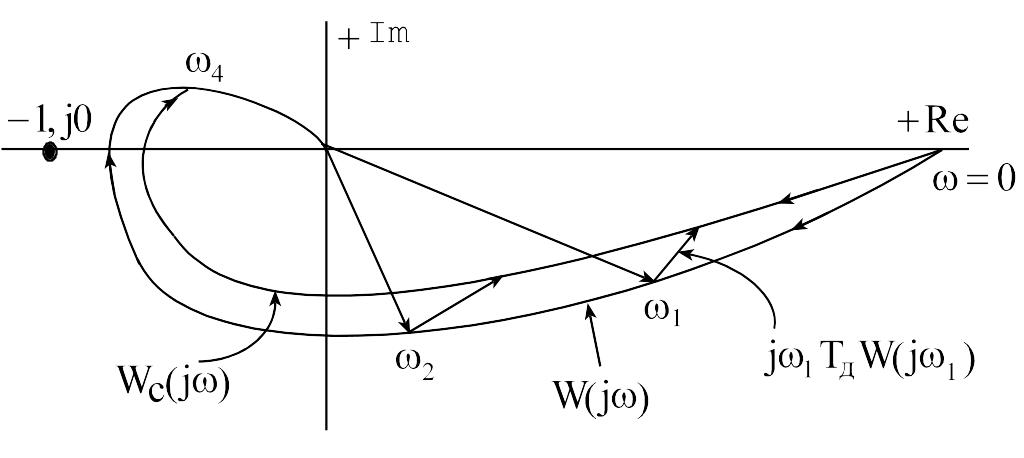
Рисунок 8.2 - АФХ исходной САУ и при введении производной

получим систему, на выходе мгновенно воспроизводящую входной сигнал. Передаточная функция замкнутой системы:

.

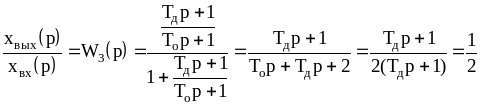В итоге система превращается в усилительное звено, мгновенно воспроизводящее во времени и по форме входной сигнал.

Для системы с после коррекции получаем . Характеристическое уравнение замкнутой САУ: . Условие устойчивости по Гурвицу .

Предельное значение , при котором исходная система приходит к границе устойчивости: . Для скорректированной САУ , т.е. . Это позволяет увеличить коэффициент усиления разомкнутой системы и таким образом, снизить статическую погрешность САУ.

8.2 Введение интеграла в закон регулирования

Пусть на рисунке 8.1 в качестве корректирующего звена используется интегрирующее с . Тогда передаточная функция разомкнутой скорректированной системы .

Введение корректирующего интегрирующего звена деформирует АФХ ра­зомкнутой системы:

К каждому вектору исходной АФХ добавляется вектор

, который направлен вод углом 90° по часовой стрелке по отношению к основному. Кроме того, величина его тем больше, чем меньше . Как видно из рисунка 8.3, наличие интегрирующего зве­на в законе управления всегда деформирует АФХ исходной системы в сторону ее разбухания.

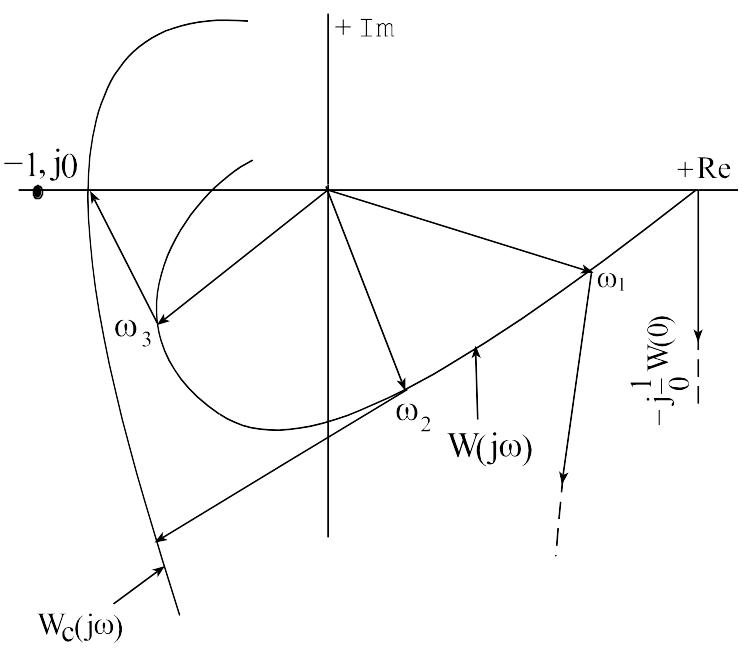
Рисунок 8.3 - АФХ исходной САУ при введении интеграла

При этом запас устойчивости САУ по модулю и фазе уменьшается.

Для выяснения влияния интегрирующей составляющей на статичес­кую погрешность обратимся опять к рисунку 8.1. Здесь статическая погрешность . Передаточная функция замкнутой САУ между и входным сигналом - для не скорректированной системы.

Пусть , тогда

(8.2)

Для скорректированной системы

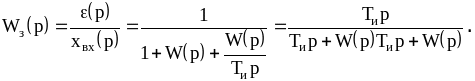
Предположив, как и в первом случае , получим

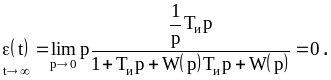(8.3)

Введение интегральной составляющей исключает статическую ошибку регулирования.

Введение звеньев в цепь прохождения основного сигнала называ­ется последовательной коррекцией. Она проста, но чувствительна к помехам и требует дополнительных усилителей. Если корректирующее звено вводится в цепь обратной связи, то коррекция называется параллель­ной. Она уменьшает нестабильность и нелинейность характеристик отдельных элементов.

Питание цепей обратной связи осуществляется с выхода последую­щих элементов, имеющих большую мощность и не вызывает затруднений. Высокочастотная составляющая фильтруется звеньями прямой связи, поэтому параллельная коррекция нечувствительна к помехам. Однако она требует применения громоздких устройств (трансформаторы, тахогенераторы и т.д.).

8.3 Создание инвариантных САУ

Основоположником теории инвариантности является В.Г. Щипанов, опубликовавший свою первую работу в 1939 году. Однако она подверг­лась резкой критике многих ученых (Н.Н.Вознесенского, А.В.Михайлова, Е.Л.Николаи, Ф.Ф.Гантмахера). Расхождение во взглядах уче­ных основывалось на том, что они смешивали две различные постановки задачи. В.Г. Щипанов решал задачу об устранении вынужденной сос­тавляющей отклонения регулируемой величины, а в критических работах рассматривалась задача о тождественном равенстве нулю общего решения, т.е. суммы свободной и вынужденной составляющей.

В настоящее время существует три направления создания инвари­антных САУ:

1. Системы с одной регулируемой величиной, работающие по отк­лонению. В таких системах условие абсолютной инвариантности достигается при коэффициенте усиления разомкнутой САУ равном бесконеч­ности.

2. Создание комбинированных систем.

3. Использование принципа двухканальности Б.Н. Петрова в многосвязных системах.

САУ называется инвариантной по отношению к возмущающему воз­действию, если после завершения переходного процесса, определяе­мого начальными условиями, регулируемая величина и ошибка систе­мы не зависят от этого воздействия.

САУ называется инвариантной по отношению к задающему воздейст­вию, если после завершения переходного процесса, определяемого начальными условиями, ее ошибка не зависит от этого воздействия.

При нулевых начальных условиях

где - передаточная функция САУ,

В соответствии с правилами определения оригинала функции при отсутствии кратных корней

(8.4)

где - корни полинома ; - корни полинома .

Вынужденная составляющая будет тождественно равна нулю, если:

- входное воздействие отсутствует;

- условие абсолютной инвариантности (равенство нулю пе­редаточной Функции замкнутой САУ по отношению к возмущающему воз­действию).

Корни совпадают с корнями и и сомножители, соответст­вующие им, можно сократить. Этот случай соответствует частичной инвариантности, когда САУ будет инвариантна только к определенному виду возмущений.

Под частичной инвариантностью (до ) понимается не тождественное равенство нулю вынужденной составляющей, а приближенное, мерой выполнения которого является некоторая величина .

8.4 Создание комбинированных САУ

Основным методом, используемым при создании инвариантных систем, является применение комбинированного управления, при котором управляющее воздействие реализуется не только по отклонению регулируемой величины, но и по возмущению, для этого измеряется ос­новное возмущающее воздействием и сигнал через корректирующее зве­но вводится в САУ.

При этом реализуется принцип двухканальности и не возникает противоречия между устойчивостью и инвариантностью, как это имеет место в одноконтурных системах, реализующих условие инвариантнос­ти за счет повышения коэффициента усиления системы. Введение сиг­нала по задающему или возмущающему воздействиям (рисунок 8.4,8.5) позволяет получить абсолютную инвариантность САУ. В терминах пе­редаточных функций ранее данные определения инвариантности можно сформулировать следующим образом:

САУ инвариантна к задающему воздействию, если ее передаточ­ная функция по отношению к нему равна единице;

САУ инвариантна к возмущающему воздействию, если ее передаточ­ная функция по отношению к нему равна нулю.

Условия реализации абсолютной инвариантности легко проследить на примерах (рисунок 8.4,8.5).

Для системы (рисунок 8.4)

Отсюда (8.5)

Для системы (8.5):

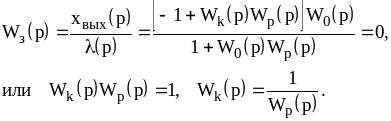(8.6)

Введение дополнительных воздействий не изменяет характеристического уравнения замкнутой САУ, поскольку корректирующие звенья не входят в замкнутый контур прохождения сигнала. При этом не бу­дет нарушаться не только устойчивость САУ, но и сохраняться оценки качества переходного процесса, базирующиеся на использовании кор­ней характеристического уравнения.

Однако при создании инвариантных САУ очень остро возникает вопрос физической реализуемости . Поскольку для физической реализации передаточной функции 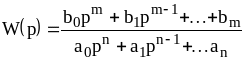необходимо, чтобы , то при реализации условия абсолютной инвариантности сталкиваются с затруднениями реализации производных. Например, если

Это звено физически реализуемо, . Это реальное дифференцирующее звено.

При

Если регулятор обладает астатизмом -го порядка, то должно реализовать производную -го и выше порядков и не иметь производных до порядка, что физически невозможно реа­лизовать.

В этом случае реализуется частичная инвариантность за счет замены идеальных дифференцирующих звеньев реальными.

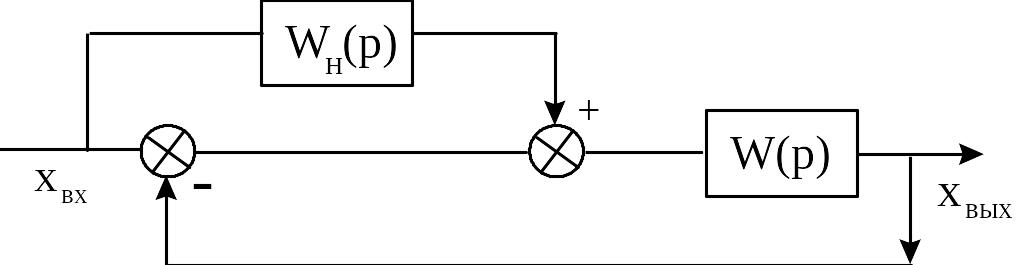
Рисунок 8.4 - Реализация инвариантности по заданию САУ

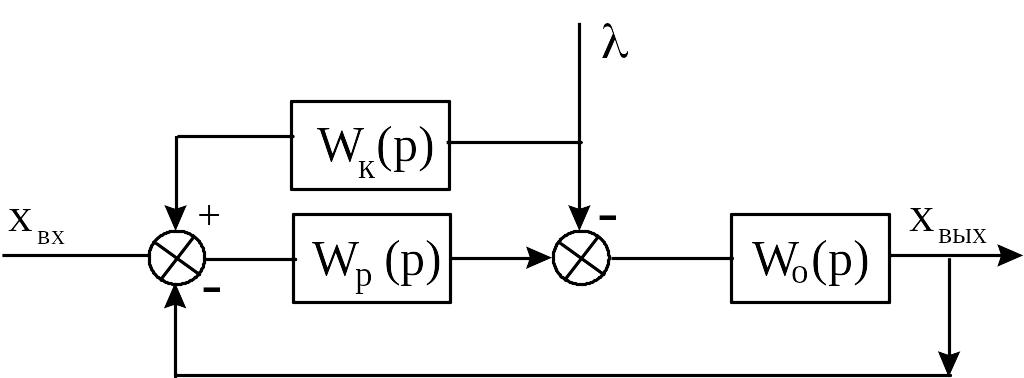
Рисунок 8.5 - Реализация инвариантности по возмущению САУ

Можно реализовать инвариантность по нескольким возмущениям, но это практически сложно.

Для САУ, описываемых дифференциальными уравнениями 1-го и 2-го порядка, когда необходимое условие устойчивости (положи­тельность коэффициентов характеристического уравнения) является и достаточным, можно корректирующие звенья не устанавливать, а увеличивать коэффициент усиления разомкнутой САУ. При этом (рисунок 8.4):

Коэффициент усиления разомкнутой САУ равен . Для того, чтобы САУ была инвариантна к задающему воздей­ствию, необходимо, чтобы

. Это отношение будет стремиться к единице при . При этом САУ будет инвариантна и к возмущающему воздействию (рисунок 8.5).

Если

8.5 Многомерные автоматические системы

Принципиальной особенностью многомерных автоматических систем (MAС) является наличие перекрестных межконтурных связей. Связи осуществляются как через моменты САУ, так и через внутренние каналы в объекте регулирования, имеющем несколько регулируемых величин (давления, температура, концентрация и т.д.).

Структурная схема объекта с двумя связанными регулируемыми величинами изображена на рисунке 8.6.

Связь выходных и входных величин можно представить с помощью передаточной матрицы.

В матричной форме уравнение объекта записывается так:

, (8.7)

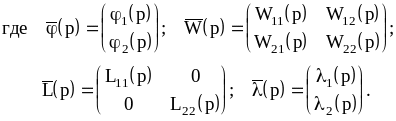
Как видно из рисунка 8.6 и уравнения (8.7), каждой регулируе­мой величине можно поставить в соответствие свой регулирующий орган и выявить прямые или сепаратные связи (каналы). Они обыч­но выделяются по признаку интенсивности воздействия или быстродействию. Каждый сепаратный канал образует совместно с регулято­ром свою сепаратную систему.

Канал воздействия, берущий начало в одной сепаратной системе и приложенный к другой, называется перекрестной связью.

Перекрестные связи, существующие вследствие физических осо­бенностей объекта или устройства, называются естественными. Искусственно вводимые перекрестные связи, служащие для придания МАС желаемых свойств, называются корректирующими. При этом связь называется прямой перекрестной, если сигнал передается в направлении прохождения основного сигнала, и обратной перекрестной связью, если сигнал передается против прохождения основного сигнала.

Матричное звено характеризует передачу воздействия в линей­ной динамической системе и отражает зависимость каждого выхода системы от каждого ее входа.

Совокупность входных сигналов образует вектор входа, выходных - вектор выхода.

Для многосвязного регулятора входным вектором будет , выходным . Уравнение регулятора в матричной форме

. (8.8)

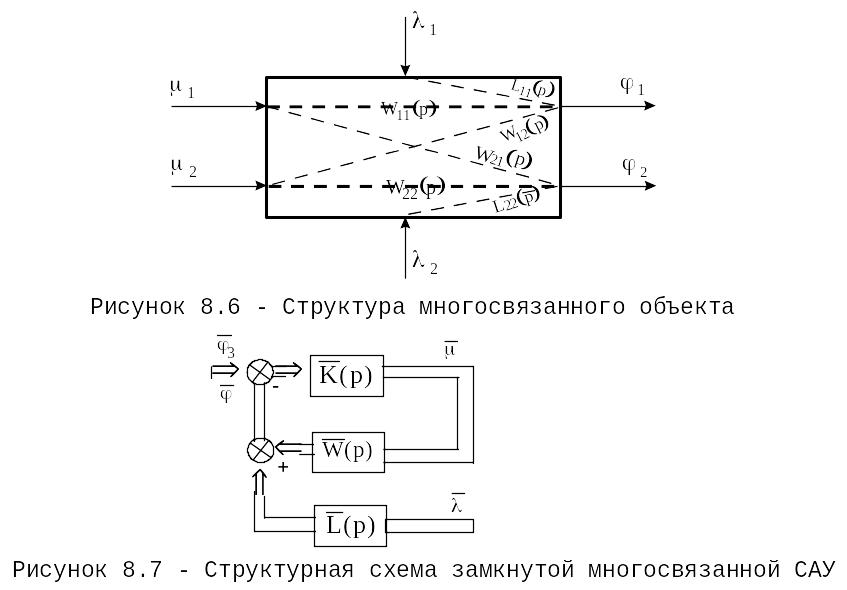
Структурная схема замкнутой МАС изображена на рисунке 8.7.

Правила преобразования матричных структур имеют нормальное сходство с правилами преобразования обычных структурных схем, однако некоммутативностъ произведения матриц предопределяет некоторые особенности правил преобразования.

1. Передаточная матрица последовательно включенных звеньев равна их произведению в обратной последовательности.

2. Передаточная матрица параллельно включенных матриц равна их сумме. Суммировать можно только матрицы одного порядка, при­чем сумма обладает переместительным и сочетательным законом.

3. Для встречно-параллельно включенных звеньев (рисунок 8.7) запи­шем соотношения:

; (8.9)

. (8.10)

Решая совместно уравнения (8.9) и (8.10), получаем

или (8.11)

где - единичная матрица; - характеристическая матрица замкнутой многосвязной автоматической системы.

Для получения передаточной матрицы МАС по задающему и воз­мущающему воздействию необходимо все слагаемые выражения (8.11) слева домножить на .В итоге получим

Передаточная матрица по задающему воздействие:

(8.12)

Передаточная матрица по возмущающему воздействию:

(8.13)

Для обеспечения абсолютной инвариантности MAС необходимо добиться:

Иногда очень желательной является независимость регулируе­мых величин друг от друга, т.е. изменение регулируемой величины не приводило к изменению каждой из « » регулируемых величин. Такой случай инвариантности называется автономностью по И.Н.Вознесенскому.

Очевидно, что развязать контуры регулирования по задающим воздействиям можно, обеспечив диагональность передаточной мат­рицы . Условием автономности будет равенство нулю всех элементов этой матрицы, кроме диагональных.

Аналогично можно MAС сделать автономной по возмущающим воз­действиям. Для этого необходимо, чтобы диагональной была матрица .

Если рассмотреть , то можно установить, что она может быть диагональной только тогда, когда будет диагональной. В самом деле, если матрица диагональная, то диагональными будут и матрицы , и, следовательно .

Таким образом, условие автономности МАС, разомкнутой по основным обратным связям, является необходимым и достаточным условием автономности замкнутой МАС по задающим воздействиям.

Благодаря наличию в МАС естественных перекрестных связей ус­ловия инвариантности можно добиться без введения дополнительных связей, принцип двухканальности здесь осуществляется структурой самой системы.

9 НЕЛИНЕЙНЫЕ СИСТЕМЫ

Линейная теория, используемая для анализа и синтеза линей­ных моделей систем управления, обычно бывает полезна на первой стадии исследований для приближенной оценки их качества и не может охватить всего многообразия движений, наблюдающихся в реальных системах.

В то время как линейная теория автоматического управления приобрела строгую законченную форму, теория нелинейных систем до сих пор остается предметом исследований многих российских и зарубежных ученых. Это объясняется тем, что многие явления, специфичные для нелинейных систем, не могут быть объяснены на ос­нове общих методов исследования, и каждая задача требует инди­видуального подхода. Поэтому для решения проблем нелинейной теории привлекается различный математический аппарат, тем не менее многие важные практические вопросы далеко не разрешены.

Можно утверждать, что практически все системы управления нелинейные. Но, допуская некоторые идеализации, их свойства в первом приближении могут быть описаны линейными дифференциаль­ными уравнениями, что облегчает процесс исследования. Однако не все реальные звенья допускают линеаризацию обычным способом (разложением в ряд Тейлора, методом средних или методом наименьших квадратов) без потери при исследовании важнейших свойств системы. В этом случае одно или несколько звеньев сис­темы описывается нелинейными зависимостями, а остальные нелинейными. Вся такая система относится к классу нелинейных и исследуется соответствующими методами, описанными ниже.

10.1 Основные типы нелинейностей

Существует множество разнообразных нелинейных описаний, поскольку к ним относится все, что чем-либо отличается от ли­нейного (нелинейности в непрерывных системах с постоянными па­раметрами, с переменными во времени параметрами, в дискретных системах, системах с распределенными параметрами и т.д.).

Наиболее часто встречающиеся нелинейности можно классифи­цировать следующим образом.

Нелинейность релейного типа, рисунок 9.1. Обозначив через -выходную, а через - входную величину релейного элемента, в общем случае можно записать

.

(9.1)

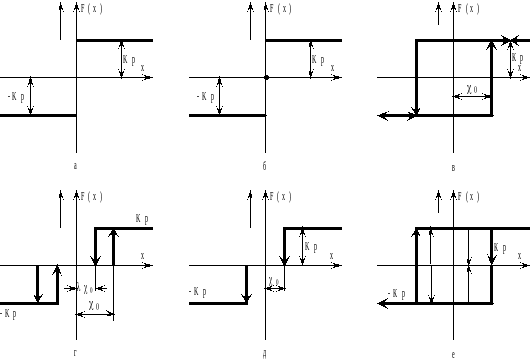
Рисунок 9.1 - Характеристики релейных элементов

На рисунке 9.1.а, изображена характеристика релейного элемента без среднего положения (двухпозиционного), а на рисунке 9.1,б трехпозиционного (со средним положением). Связь выходной и входной величин для них следующая: для 9.1,а -

(9.2)

для 9.1,б

(9.3)

Релейный элемент может иметь зону нечувствительности (рисунок 9.1,д). Тогда

(9.4)

Если коэффициент возврата релейного элемента не равен единице, рисунок 9.1,г, то характеристика оказывается неоднозначной,

(9.5)

Релейный элемент может иметь положительный гистерезис, рисунок 9.1.в, и отрицательный гистерезис, рисунок 9.1,е. Особенность релейных элементов с гистерезисом в том, что уравнение, опи­сывающее связь между выходной величиной и входной, включает параметр , характеризующий состояние релейного элемента после последнего переключения.

Для описания релейного элемента с отрицательным гистерези­сом, рисунок 9.1,е, необходимо знать не только величину входного сигнала, но и скорость его изменения. Обозначим ,тогда

(9.6)

Характеристики релейных элементов могут быть несимметричными, или релейно-импульсными, когда при превышении некоторого уровня входного сигнала подается импульс определенной длитель­ности, а в случае превышения другого уровня - импульс другой длительности и т.д. При достижении входным сигналом больших ве­личин включается релейный элемент, подающий сигнал постоянной величины.

Нелинейности непрерывных статических характеристик, рисунок 9.2.

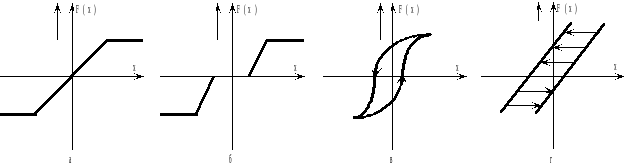
Рисунок 9.2 - Статические нелинейности

Они записываются в форме (9.1) и могут задаваться анали­тически в виде степенных и других функций. Характеристика с насыщением изображена на рисунке 9.2,а, с нечувствительностью и насыщением на рисунке 9.2,б, с петлей гистерезиса - на рисунке 9.2,в, с зазором - на рисунке 9.2,г.

Динамические нелинейности, которые описываются нелинейны­ми дифференциальными зависимостями. Примером может служить не­линейное введение производной наряду с самой величиной, изме­нение постоянной времени в зависимости от входной величины, нелинейное трение.

Нелинейность переменной структуры, связанная с изменением значения переменной . В этом случае система, состоящая из линейных звеньев, создает нелинейное устройство, реализую­щее определенную функцию переключения , которая, например, будет равна

(9.7)

Нелинейности логического типа, когда элемент, имеющий несколько входов, выдает ступенчатый сигнал (1,0,-1) в зависимости от определенных логических комбинаций свойств входных величин.

Релейные автоматические системы

Релейные системы относятся к наиболее простому классу нелинейных систем, поскольку благодаря специфике релейного элемента, создающего воздействия на линейную часть системы в виде прямоугольных импульсов постоянной высоты, исследование их сво­дится к исследованию линейной части, подверженной указанным импульсам.

Управляющее воздействие, приложенное к линейной части системы, можно представить в виде суммы воздействий простейшего вида, а реакцию линейной части найти, применив принцип суперпозиции, как сумму реакции на каждое из них.

Релейные системы, отличаясь простотой, имеют иногда лучшие динамические свойства, чем другие. Создание бесконтактных релейных элементов, допускающих изменение параметров, позволяет придавать системе новые свойства. Поскольку при наличии рассо­гласования между заданным и действительным значением регулируе­мой величины управляющее воздействие всегда будет максимальным, то, естественно, быстродействие системы станет большим, однако в ней возникнут незатухающие колебания (автоколебания). Как правило, автоколебания нежелательны, но в некоторых системах они являются основным рабочим режимом.

Если на релейную систему подействовать периодическими воз­действиями, то при определенных условиях (условия захватывания) ранее существующие в ней автоколебания устраняются, но при этом возникают вынужденные колебания с частотой, равной частоте внешнего воздействия.

При достаточно большой частоте вынужденные колебания будут иметь малую амплитуду, допустимую по технологическим требованиям.

Наличие автоколебаний ослабляет отрицательное влияние на динамику системы сухого трения, гистерезиса и придают ей свой­ства пропорциональности, линеаризуют ее.

Применяя внутренние обратные связи, можно получать скользя­щие режимы и строить на их основе частотно-импульсные системы.

Исследовать релейную систему удобнее, если отдельно выде­лять релейный элемент и линейную часть, а все возмущающие воз­действия приводить к входу релейного элемента. В итоге получим структурную схему, представленную на рисунке 9.3, где обозначе­ны в изображениях Лапласа

- возмущения, приведенные к входу релейного элемента;

- входная величина релейного элемента;

- выходная;

-регулируемая величина.

Для линейной части	(9.8)
уравнение замыкания ;	(9.9)
уравнение релейного элемента	(9.10)

где - символ прямого преобразования Лапласа.

Рисунок 9.3 - Структурная схема релейной системы

Исключая промежуточные переменные и из сис­темы уравнений (9.8), (9.9), (9.10), получаем уравнением замк­нутой системы

(9.11)

или, если нас интересует регулируемая величина

.

(9.12)

Как видно из уравнений (9.11) и (9.12), их нельзя разрешить в явном виде относительно и , поскольку они входят в качестве аргумента нелинейной функции и, следовательно, не могут быть использованы для построения переход­ного процесса в релейной системе.

9.2 Построение переходных процессов в релейных системах

Линейная часть релейной системы подвержена воздействию прямоугольных импульсов постоянной высоты. Знак, длительность и расположение импульсов зависят от внешнего воздействия. На основании принципа наложения результирующую реакцию можно най­ти простым суммированием реакций системы на каждое воздействие порознь.

Для определенности всегда будем считать, что управляющий сигнал впервые проходит пороговое значение, уменьшаясь, т.е. (рисунок 9.4).

Под пороговым значением управляющего сигнала понимают та­кое значение, при котором выходная величина релейного элемента всякий раз изменяется скачком. Например, для релейного элемента, изображенного на рисунке 9.1,д, пороговое значение , для рисунков 9.1,а и 9.1,б .

Условие позволяет выбирать знак неравенства условия надлежащего направления переключения.

Рассмотрим систему с релейным элементом (рисунок 9.1,а) без гистерезиса и зоны нечувствительности (идеальным релейным элементом ).

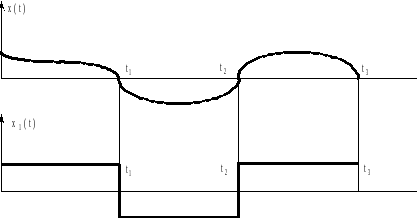
Рисунок 9.4 - Графики входного и выходного сигналов релейного элемента

Моменты переключения ( ...) есть те моменты, в

которые x(t) проходит пороговые значения, т.е. эти моменты являются корнями уравнения

. (9.13)

Условие (9.13) есть условие надлежащих моментов переключения. Кроме того, для последовательного чередования направлений переключений необходимо, чтобы выполнялось условие

(9.14)

или

(9.15)

Условия (9.14) и (9.15) называются условиями надлежащих направлений переключения.

Изображения любого из прямоугольных импульсов можно записать так:

(9.16)

где

- значение амплитуды прямоугольного импульса на выходе релейного элемента.

Изображение управляющего воздействия есть сумма изображений всех импульсов

Следовательно,

(9.17)

Поскольку

где - символ обратного преобразования Лапласа,

- переходная функция линейной части системы,

то и

(9.18)

Принимая во внимание (10.18) из выражения (10.17), получаем

(9.19)

Итак, для отдельных участков переходного процесса на ос­новании (10.19) получаем

Легко заметить, что выражение для можно записать в виде:

(9.20)

Из выражений (9.18), (9.19), (9.20) следует, что для построения переходного процесса в релейной системе необходимо иметь переходную характеристику линейной части системы и знать момен­ты переключения . Поскольку априори неизвестна, то аналитически вычислить нельзя. Наиболее простой способ на­хождения - это графический.

Если на графике изобразить и нанести функцию (рисунок 10.5), то точка их пересечения даст значение . Начиная с момента , откладываем величину и складываем ее с так, что при t₁<t<t₂ получаем . Абсцисса точки пересече­ния с даст значение t₂ и т.д. Продолжая указанную последовательность действий, строим переходный процесс в системе при заданном входном воздействии.

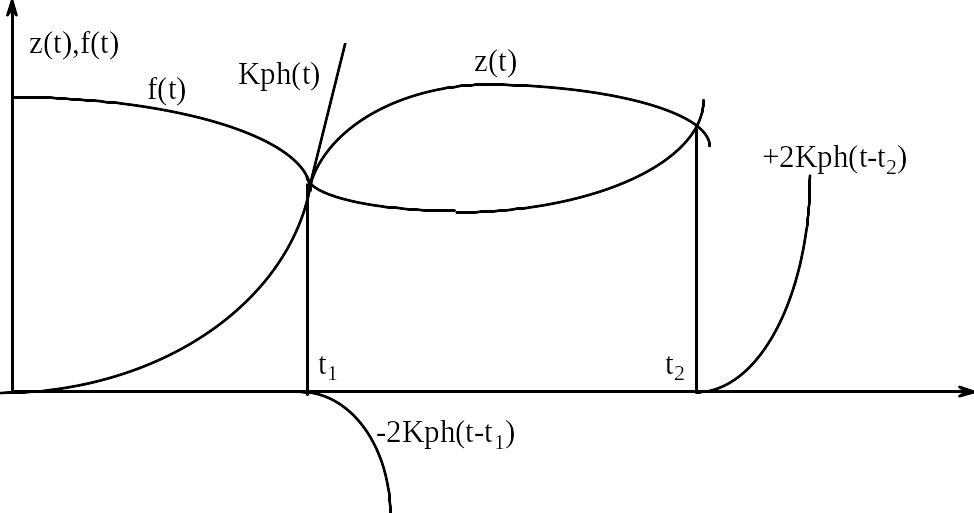
Рисунок 9.5 - Графический способ определения

Если релейный элемент имеет гистерезис (рисунок 10.1,в), то условие надлежащих моментов переключения будет таким:

(9.21)

a условие надлежащих направлений переключения останется преж­ним (9.14).

Как видно из рисунка 9.6, последовательность импульсов, воз­действующих на линейную часть, имеет прежний вид, поэтому и вы­ражение для вычисления выходной величины системы остается преж­ним.

Если характеристика релейного элемента смещена (рисунок 9.7), то можно считать, что к линейной части дополнительно приложено постоянное возмущение

(9.22)

Для релейного элемента с зоной нечувствительности и гисте­резисом (рисунок 9.1,г) условия надлежащих моментов переключения принимают вид (рисунок 9.8):

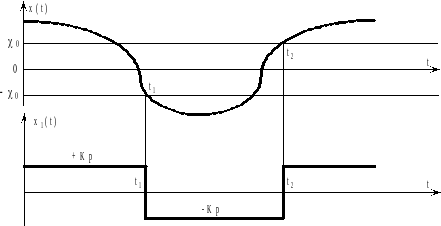
Рисунок 10.6 - Последовательность управляющих импульсов при наличии зоны нечувствительности

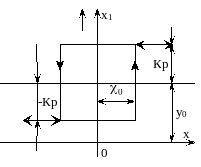
Рисунок 10.7 - Характеристика реле со смещением

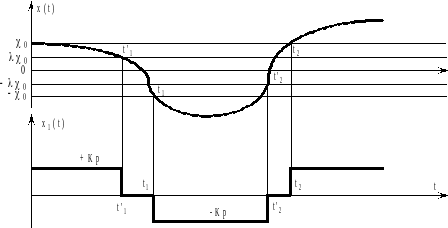
Рисунок 9.8 - Характеристика управляющих воздействий при наличии зоны нечувствительности и гистерезиса

(9.23)

а условия надлежащих направлений

(9.24)

Как следует из рисунка 9.8, в данном случае форма прямоуголь­ных импульсов, действующих на линейную часть системы, изменя­ется по сравнению с ранее рассмотренной. В промежутки времени от до отсутствует воздействие на линейную часть.

Если рассуждать таким же образом, как и в предыдущих слу­чаях, то можно записать выражения для выходной величины систе­мы в следующем виде:

(9.25)

и

(9.26)

Выражение (9.25) соответствует наличию управляющего воз­действия на систему, а выражение (9.26) - отсутствию управляю­щего воздействия.

Рассмотренный метод построения переходных процессов может быть использован только в том случае, если заданы численные значения параметров релейного элемента и линейной части систе­мы. Он применим к системам с распределенными параметрами, запаздыванием и т.д., если найдена каким-либо способом переходная характеристика линейной части. Однако этот метод не дает возможности найти общие условия устойчивости и возникновения различных режимов, существующих в релейных системах.

При машинном методе построения переходных процессов непрерывную часть системы следует представить в виде системы дифференциальных уравнений первого порядка (в форме Коши). Релейную характеристику описывают системой логических выражений, соответствующих условиям (9.2 - 9.6), которые необходимо дополнить уравнением замыкания .

9.3 Устойчивость нелинейных систем

Основополагающей работой в этой области является работа А.М. Ляпунова (1892) "Общая задача об устойчивости движения". Однако наибольшее значение для исследования устойчивости не­линейных систем имеет так называемый второй (прямой) метод Ляпунова, основанный на использовании некоторой функции, называемой функцией Ляпунова. В своей работе он указал способ по­строения такой функции лишь для линейных систем. Для нелиней­ных систем общего метода определения функции Ляпунова нет, по­этому можно подобрать несколько функций, каждая из которых даст свои условия устойчивости, т.е. второй метод Ляпунова позволя­ет получить лишь достаточные условия устойчивости. Сложность метода не позволяла его использовать почти 60 лет.

В настоящее время существует большое число различных определений понятия устойчивости. Это прежде всего понятие асимптотической и абсолютной ус­тойчивости (А.И. Лурье, В.Н. Постников,1945 г.) устойчивости в малом, большом, целом (Я.3.Цыпкин, В.М. Попов - румынский уче­ный, 1959 г.); технической или практической устойчивости на конечном интервале времени (К.А. Карагаров, А.Г.Пилютин.1962г.); устойчивость по Лагранжу (Ж.П.Ла-Салль,С.Лефшец,1964 г.), ус­ловной устойчивости (Ж.П.Ла-Салль,1964 г.) гиперустойчивости (В.М.Попов,1960 г.).

В настоящее время существуют аналитические и частотные методы исследования нелинейных систем. Сложность аналитическо­го исследования привели к разработке критериев (Я.3.Цыпкина, В.М. Попова) позволяющих упростить решение задачи.

Общие положения об устойчивости нелинейных систем

При отсутствии возмущающих воздействий уравнения динами­ки для нелинейной системы -го порядка в общем виде в нор­мальной форме Коши имеют вид:

(9.27)

Пусть есть невозмущенное движение системы, а - отклонение возмущенного состояния системы, тогда

(9.28)

где - возмущенное движение системы, определяемое уравнениями (9.27) при определенных начальных условиях .

Уравнение возмущенного движения в отклонениях запишется в виде:

(9.29)

В общем случае вид уравнений (10.29) зависит от вида установив­шегося процесса , поскольку (9.29) получается из (9.27) подстановкой (9.28). Это могут быть гармонические коле­бания, линейная временная функция и т.д.

Невозмущенное движение называется устойчивым, если задав "трубку" -мерного сечения , можно подобрать в начальный момент такую область начальных условий , зависящую от , что с увеличением возмущенное движе­ние не выйдет из заданной трубки .

Невозмущенное движение будет неустойчивым, если указанное условие не выполняется хотя бы для одного .

Если условия определения выполнены и при то невозмущенное движение называется асимптотически устойчивым.

Если же при после любых начальных отклонений, то система называется устойчивой в целом.

Абсолютно устойчивой называют асимптотически устойчивую систему в целом внутри определенного класса нелинейностей.

Таким образом, в отличие от линейных систем, устойчивость нелинейных определяется величиной возмущающего воздействия (отклонения координат состояния).

Функция Ляпунова

Знакоопределенной функцией называется такая, которая во всей рассматриваемой области, содержащей начало координат, сохраняет один и тот же знак и обращается в нуль только в начале координат. Она может быть положительно определенной или отрицательно определенной. Функция назы­вается знакопостоянной, если имеет один и тот же знак, но обращается в нуль не только в начале координат, например:

Знакопеременной называется функция, не сохраняющая знака в рассматриваемой области.

Согласно критерию Сильвестра любая квадратичная форма бу­дет знакоопределенной (положительно), когда все главные диаго­нальные миноры матрицы ее коэффициентов будут положительными.

Например:

, обращающаяся в нуль в начале координат, называ­ется функцией Ляпунова, если она знакоположительна.

Производная функции Ляпунова:

(9.30)

Учитывая (10.29), можно записать:

(9.31)

также является функцией координат системы.

Поскольку ,а то

(9.32)

т.е. производная функции Ляпунова по времени представляет со­бой скалярное произведение градиента этой функции на вектор фазовой скорости.

Скалярным произведением двух векторов называется , или, если векторы заданы в декартовых коор­динатах, то

и

Вектор grad  перпендикулярен и направлен в сторону возрастания . Если , то с вектором grad  составляет острый угол и фазовая траекто­рия пересекает в сторону увеличения. Если , угол между grad  и тупой, (ко­синус отрицательный) и фазовая траектория идет в сторону умень­шения . Если для системы уравнений (9.29) существует знакоопределенная функция , производная которой является знакопостоянной противоположного знака, то решение систе­мы устойчиво, если - знакоопределенная, то решение системы будет устойчивым асимптоти­чески. Действительно, если , то фазовая траектория может остаться на поверхности . Если же , фазовая траектория будет монотонно убывающей и x(t)0 при .

Пример:

Подставив и , имеем

При - знакоопределенная отри­цательная функция. При этом остается положительной, следовательно исходная нелинейная система асимптотически устойчива.

9.4 Устойчивость релейных систем

При рассмотрении устойчивости релейных систем воспользуем­ся определением, приведенным Я.3.Цыпкиным. Это объясняется не только удобством формулировки (существует большое число различ­ных определений понятия устойчивости), но и распространенностью релейных систем в классе нелинейных.

Нелинейная система будет устойчивой, если для всякого за­данного числа можно найти такое число , что для всех исчезающих воздействий таких, что входная величина нелинейного элемента удовлетворяет неравенству для всех . Если потребовать, чтобы то такая система называется асимптотически устойчивой. Воздействие называется исчезающим, если комбинация и абсолютно интегрируема, т.е.

.

Это понятие асимптотической устойчивости несправедливо для нелинейных элементов с зоной нечувствительности. В этом слу­чае следует считать положение равновесия устойчивым, если

где - любое значение, принадлежащее зоне нечувствительности.

Итак, если на нелинейную систему действует ограниченное по модулю внешнее воздействие, то в асимптотически устойчивой системе существует вынужденное движение, ограниченное по модулю, и, кроме того, отклонение от вынужденного движения стремится к нулю с течением времени. Если условия асимптотической устойчивости выполняются при малых отклонениях от положения равновесия, то система устойчива в малом. Если условия устойчивости выполняются при любых конечных значениях (), то система устойчива в большом. И, наконец, если автоматическая система асимптотически устойчива при любых (), то она ус­тойчива в целом.

Особенность нелинейных систем - в том, что система может быть асимптотически устойчивой в малом, но условия асимптоти­ческой устойчивости в большом могут не выполняться.

Невозможность получения решения в большинстве случаев для систем выше второго порядка привела к разработке методов на­хождения достаточных условий устойчивости нелинейных систем без точного решения описывающих их уравнений.

При отсутствии зоны нечувствительности у нелинейного элемента его выходной сигнал стремится к нулю только тог­да, когда частота переключений в системе неограниченно возрас­тает.

Для определения условия устойчивости нелинейной системы в малом рассмотрим наиболее тяжелый случай, когда нелинейный эле­мент имеет вид идеального реле. В этом случае нелинейную сис­тему можно представить состоящей из линейной части и усилителя с бесконечным коэффициентом усиления. Для устойчивости такой системы необходимо, чтобы выполнялось условие устойчивости ли­нейной системы при неограниченном возрастании ее коэффициента усиления.

Если на рисунке 10.3 предположить, что у нелинейного элемента коэффициент усиления К, а , то передаточ­ная функция замкнутой системы будет равна

Отсюда - характеристическое уравнение замкнутой системы

(9.33)

Условием устойчивости нелинейной системы в малом являет­ся отрицательность действительных частей корней характеристи­ческого уравнения (9.33).

При получаем предельную систему, характеристичес­кое уравнение которой .

Найдем критерий устойчивости нелинейных систем, позволяю­щий по или линейной части судить об устойчивос­ти замкнутой системы в малом. Для этого воспользуемся - раз­биением по основному параметру .

Полагая в уравнении (9.30) , получаем .

Для устойчивости системы необходимо, чтобы при больших , включая , точка принадлежала отрезку устойчи­вости, который представляет собой отрезок вещественной оси на комплексной плоскости, находящийся в заштрихованной области. На комплексной плоскости штрихуется область, расположенная слева от при возрастании . Поскольку велико, то нас интересует поведение только при больших значениях . Если разложить по степеням , т.е.

(9.34)

то поведение ее при больших  определяется первыми членами разложения. приближается к нулю по прямой под углом к действительной оси.

На рисунке 9.9 изображены различные варианты при раз­личных знаках , а также различных индексах передаточной функции линейной части системы l, под которым понимается разность степеней полиномов знаменателя и числителя :

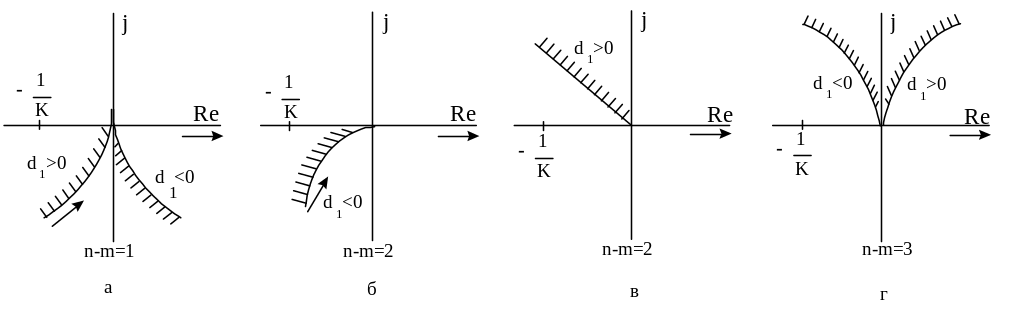
Рисунок 10.9 - Вид АФХ линейной части при различных индексах

При этом предполагается, что , поскольку всегда соответствует неустойчивости.

Анализ изображенных на рисунке 9.9 кривых показывает, что если предельная система устойчива, то и линейная система при будет устойчивой, но лишь при и . Линейная система при стремится к границе устойчивости при и и , причем, когда - велико, то линейная система бу­дет устойчивой при и неустойчивой при .

Линейная система будет заведомо неустойчивой при , если .

Коэффициенты и легко найти через коэффициенты передаточной функции линейной части системы.

(9.35)

Разложив по отрицательным степеням , получим

(9.36)

Производя перемножение в правой части, а затем приравни­вая коэффициенты при одинаковых степенях слева и справа, получаем

(9.37)

Из системы алгебраических уравнений (9.37) по правилу Крамера находим коэффициенты

(9.38)

где - определитель, полученный из правой части уравнения (9.37) заменой столбца с коэффициентами на столбец левой части системы. Поскольку нас интересуют только два коэффициента и , то из их первых двух уравнений (9.37) найдем

(9.38)

Коэффициенты и можно легко определить, если использовать следующий прием:

(9.39)

Пусть , тогда

(9.40)

Если , то

(9.41)

Итак, релейная автоматическая система будет устойчивой в малом в том случае, если нули передаточной функции находятся в левой полуплоскости комплексной плоскости, а индекс передаточной функции не превышает двух, причем

при ;

при ; .

Устойчивость предельной системы (нули передаточной функ­ции линейной части находятся в левой полуплоскости комплексной плоскости) может быть исследована любым из известных критериев устойчивости линейных систем (Гурвица, Михайлова).

9.5 Условия устойчивости нелинейной системы « в целом »

Часто в системах регулирования нелинейная характеристика не может быть точно задана или изменяться в процессе работы (например, характеристика регулирующего органа при изменении давления в питающей сети, трения в сальнике и т.д.). В таких случаях, задаваясь лишь главными свойствами нелинейности, можно найти достаточные условия асимптотической устойчивости в большом или целом.

А.M. Летовым введено определение функций класса , обладающих следующими свойствами:

- непрерывная функция,

, .

(9.42)

Этому определению удовлетворяют функции произвольной фор­мы. Использовав этот подход, можно выделить класс нелинейных функций , когда характеристика нелинейного элемента лежит внутри сектора, ограниченного прямыми линиями и рисунок 9.10

. (9.43)

Если лежит в ограниченном секторе и принадлежит классу , то асимптотическую устойчивость системы называют абсолютной устойчивостью (А.И. Лурье, В.Н. Постников).

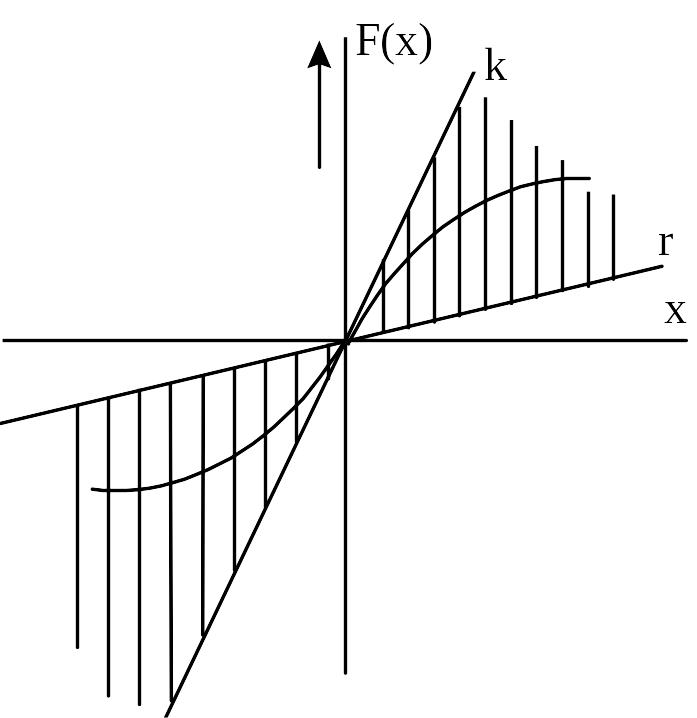
Рисунок 9.10 - График нелинейности класса

Если и , то говорят об абсолютной устойчивости в большом или некоторой области.

Работы В.М Попова стали основополагающими при исследова­нии абсолютной устойчивости нелинейных систем частотными методами. В.М. Попов доказал, что для абсолютной устойчивости по­ложения равновесия нелинейной системы, состоящей из нелинейно­го элемента с характеристикой , удовлетворяющей услови­ям (10.42) и устойчивой или нейтральной линейной частью, доста­точно, чтобы при существовало такое действительное чис­ло , при котором для всех выполнялось бы неравенство

(9.44)

Я.3.Цыпкин обобщил этот критерий и распространил на сис­темы с релейными характеристиками (разрывными). Он доказал, что для устойчивости релейной системы в целом достаточно, чтобы линейная часть системы была устойчива или нейтральна, а частотная характеристика и параметры релейного элемента удовлетворя­ли бы условию

(9.45)

где - при положительном гистерезисе;

- при отрицательном гистерезисе.

Этому критерию можно дать простую геометрическую интерпретацию. Пусть

. (9.46)

Тогда (10.45) перепишем в форме

(9.47)

В плоскости параметров и выражение (10.47) для знака равенства определяет прямую, проходящую через точку на оси абсцисс с наклоном, равным . Эта прямая называется прямой Попова и делит плоскость на две полуплоскости - правую и левую, рисунок 9.11.

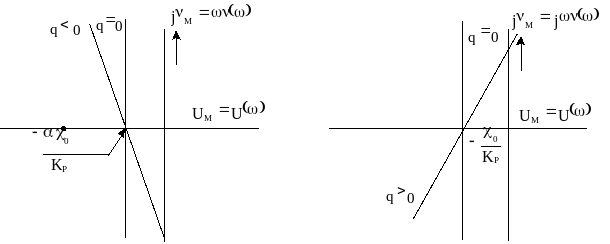
Рисунок 9.11 - Вид прямых Попова для и

Неравенство (9.45) соответствует точкам области, располо­женной справа от этой прямой.

Введем понятие модифицированной частотной характеристики линейной части релейной системы

(9.48)

где

.

Из выражения (9.46) видно, что для получения модифициро­ванной частотной характеристики достаточно в обычной изменить масштаб мнимой части в каждой точке в  раз.

Релейная система будет устойчива в целом, когда модифици­рованная частотная характеристика ее линейной части расположе­на справа от прямой Попова при , если гистерезис положительный и если гистерезис отрицательный.

Построив на комплексной плоскости модифицированную частот­ную характеристику линейной части, находим неравенство

(9.49)

где - координата точки пересечения с вещественной осью, рисунок 9.12.

Это неравенство позволяет выбирать необходимые параметры релейного элемента, обеспечиваю­щие устойчивость релейной системы в целом.

Если релейный элемент не имеет гистерезиса, то для устой­чивости релейной системы в целом необходимо, чтобы условие (9.45) выполнялось при любом .

Если релейный элемент идеальный, то автоматическая систе­ма будет устойчива в целом, когда линейная ее часть устойчива или нейтральна а частотная характеристика линейной части рас­положена в нижней полуплоскости. Эти очевидные формулировки вы­текают из условия (9.45) и общей формулировки устойчивости ре­лейных систем в целом.

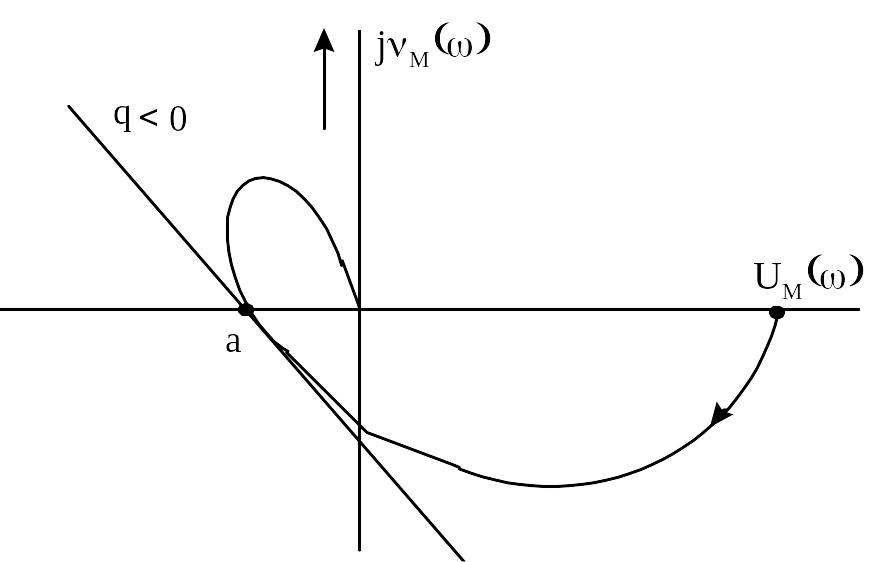
Рисунок 9.12 - Анализ устойчивости релейной САУ по критерию Цыпкина

9.6 Автоколебания в релейных автоматических системах

Следуя определению А.А.Андронова, автоколебаниями называ­ют такие периодические движения в нелинейной системе, которые возникают под действием сил, зависящих от состояния системы (а не в результате внешних периодических воздействий).

Спецификой релейных систем является то, что форма выходной величины релейного элемента в периодическом режиме предопре­делена. Поэтому исследование автоколебаний сводится к изучению воздействия периодической последовательности прямоугольных им­пульсов на линейную часть системы и отысканию их параметров, удовлетворяющих существованию периодических режимов.

Периодическая последовательность прямоугольных импульсов (рисунки 9.4, 9.6, 9.8) может быть представлена с помощью ряда Фурье в виде суммы гармонических составляющих

(9.50)

Для симметричной функции четные слагаемые от­сутствуют, поэтому

(9.51)

или в вещественной форме

(9.52)

Рассмотрим наиболее простой случай, когда используется идеальный релейный элемент (без зоны нечувствительности, рисунок 9.1,а,б). Определив коэффициенты ряда Фурье для этого случая, выражение (10.52) перепишем в виде.

(10.53)

Для нахождения реакции линейной части на сумму гармонических воздействий необходимо амплитуду каждого гармонического воз­действия умножить на модуль частотной характеристики линейной части при этой частоте, а к фазе гармонического воздействия прибавить фазу частотной характеристики системы и все произведения сложить, т.е.

(9.54)

где -амплитудно-частотная характеристика линейной части системы.

Для исследования автоколебаний в релейной системе вводится понятие годографа релейной системы

(9.55)

где мнимая равна значению выходной величины линейной части системы при с обратным знаком, а действительная часть значению производной выходной величины линейной части системы при , отнесенной к частоте  тоже с обратным знаком.

Для релейных систем с зоной нечувствительности с увеличе­нием числа условий существования автоколебаний дополнительно вводится характеристика

где характеризует отношение длительности существо­вания управлявшего воздействия одного знака к величине полупериода колебаний. Этот случай мы рассматривать не будем.

Производная берется по при

Если релейный элемент имеет зону нечувствительности, то вводятся два годографа релейной системы, которые мы не будем рассматривать.

С помощью годографов релейной системы удобно качественно и количественно исследовать влияние структуры и параметров линей­ной части системы и параметров релейного элемента на частоту и форму колебаний.

Годограф релейной системы может быть определен:

1) по частотной характеристике линейной части системы;

2) по временной характеристике линейной части системы;

3) по передаточной функции линейной части системы.

Рассмотрим методику определения по частотной харак­теристике линейной части системы. Используя (10.54), находим составляющие годографа релейной системы

(9.56)

(9.57)

Запись выражений (9.55) и (9.56) объясняется тем, что че­рез полупериод сама периодическая функция и ее производ­ная изменяют знак по сравнению со знаком, выбранным в момент начала отсчета. Подставив значения (9.56), (9.57) в выражение (9.55), получим

(9.58)

Здесь:

Выражение (9.58) указывает на метод построения годографа релейной системы по АФХ разомкнутой линейно части. Первое слагаемое для заданной частоты представляет собой частотную характеристику разомкнутой системы, в которой релейный эле­мент заменен усилителем с коэффициентом усиления, равным . Остальные слагаемые зависят от частот, кратных .

Методика нахождения иллюстрирована на рисунке 9.13.

1. Задаются значениями частот , и т.д.

2. Находят значения , ,... и т.д.

3. Строят по полученным точкам на комплексной плоскости годограф релейной системы .

Для нахождения на АФХ линейной части определяют точки, соответствующие , , , и т.д. Уменьшают ординаты точек соответственно в раз и проводят к концам уменьшенных ординат векторы из начала координат. Гео­метрически суммируя все эти векторы и умножая результат на , получают значения , рисунок 9.13.

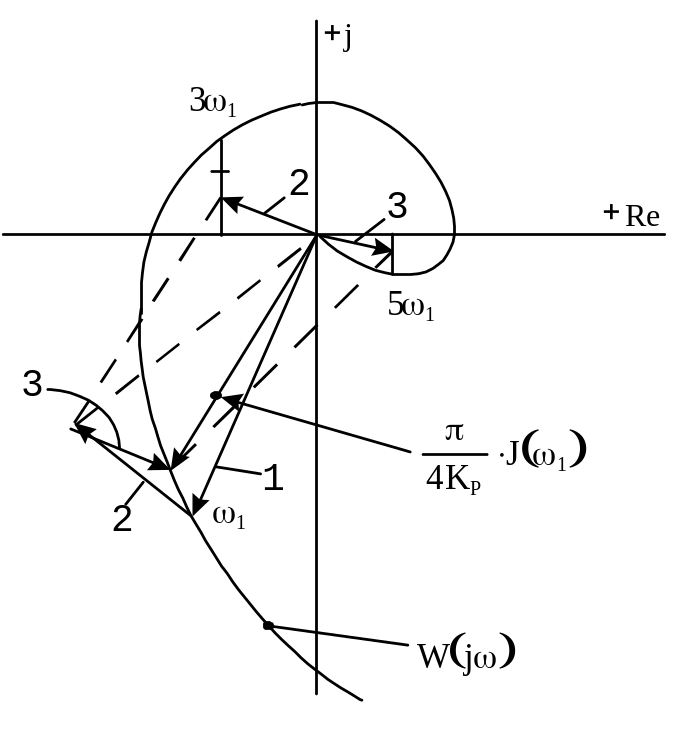
Рисунок 9.13 - Методика построения

Если известна и , то найдя на значе­ния , , и т.д. и просуммировав их, получим . Аналогично, определив по графику значения и т.д. и просуммировав их, получим . По полученным координатам легко построить .

Годограф релейной системы позволяет проверять условия существования автоколебаний и определять их частоту. Для этого на комплексной плоскости строят при изменении . Пусть релейный элемент имеет характеристику, как показано на рисунке 9.1в. Если на комплексной плоскости провести прямую, параллельную действительной оси и отсекающую на мнимой оси отрезок, равный -₀, то наличие точки ее пересечения с годографом в левой полуплоскости комплексной плоскости говорит о возможных автоколебаниях с частотой, равной частоте, соответствующей точ­ке пересечения . Для этой точки справедливы соотношения :

(9.59)

Если учесть (9.55), то (9.59) перепишем так:

(9.60)

т.е. мы получили условие надлежащего момента переключения и надлежащего направления переключения. Для точек пересечения в правой полуплоскости (рисунок 9.14) эти условия не выполняются.

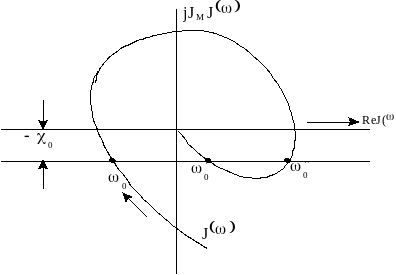
Рисунок 9.14 - Автоколебания в релейной системе

При отрицательном гистерезисе прямая заменяется на . Если в релейной системе зона нечувствительности отсутствует, то следует считать , т.е. роль этой прямой будет выпол­нять ось абсцисс.

9.7 Вынужденные колебания в релейных системах

Если на релейную систему действует периодическое

воздей­ствие, то в ней могут быть три режима работы:

1) биение между автоколебаниями и вынужденными колебания­ми;

2) вынужденные колебания, когда система синхронизируется автоматически частотой внешнего воздействия, подавляя автоколебания. Этот режим еще называют режимом принудительной синхрони­зации или захватывания;

3) режим субгармонических колебаний, при котором подавляются автоколебания и системе навязываются вынужденные колебания, частота которых составляет от частоты внешнего воздействия, где - целое положительное число.

Режим захватывания и субгармонический режим являются пе­риодическими, тогда как режим биений является непериодическим.

Пусть на систему действует внешнее воздействие вида

где - максимальное значение внешнего воздействия;

При этом входная величина релейного элемента также изменяется по периодическому закону.

Условия существования вынужденных колебаний в релейной системе с релейным элементом, изображенным на рисунке 10.1,в, пред­ставим в виде

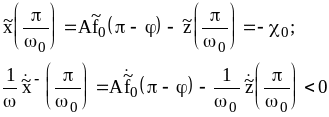
и

.

При исследовании вынужденных колебаний в релейной системе без зоны нечувствительности частота их задана, а искомой величиной является сдвиг фаз между вынужденными колебания­ми и внешним периодическим воздействием. Величина должна быть действительной и удовлетворять условиям существования вынужден­ных колебаний.

Для определения воспользуемся годографом релейной системы. Введем комплекснозначную функцию.

Если на вход подается гармоническое колебание, то

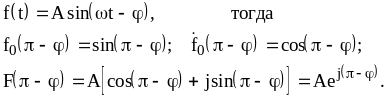
Отсюда следует, что соответствует окружности радиуса .

Рассмотрим сумму этой функции и годографа релейной системы.

Разделим на вещественную и мнимую часть сумму этих функций

При мнимая и действительная части тождествен­ны условиям надлежащих моментов и направлений переключений. По­этому условия существования вынужденных колебаний частоты можно записать в следующем виде:

Последнее условие указывает на путь определения наличия вынужденных колебаний.

Строят годограф релейной системы и на нем находят точку, соответствующую частоте . Из этой точки проводит окружность радиусом .

Условие существования автоколебаний будут выполняться для тех значений , при которых кривая пересекает прямую , в левой полуплоскости. Число найденных таким обра­зом значений определяет число периодических решений, соответствующих возможным вынужденным колебаниям.

1. При малых ( рисунок 9.15,а) точка пересечения с прямой отсутствует, вынужденные колебания частоты , которые бы подавили автоколебания, тоже отсутствуют. В систе­ме может быть режим биений либо субгармонический режим.

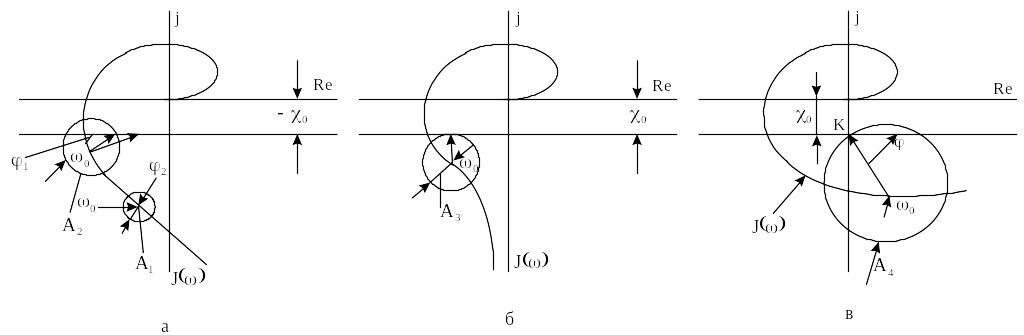
Рисунок 9.15 - Вынужденные колебания в релейной системе

2. - большое, появляются точки пересечения кривой с прямой в левой полуплоскости и, следователь­но, наблюдается режим вынужденных колебаний.

3. Если , то - касается прямой , рисунок 9.15.б.

4. Если , то кривая при некотором зна­чении , пересекает прямую лишь в точке , где прямая пересекает мнимую ось, рисунок 9.15.в. Если (рисунок 9.15.а) находится ниже прямой , то и положительны, ес­ли выше - отрицательны.

Если находится в правой полуплоскости, то опре­деляется как отрезок от точки, соответствующей до точки пересечения с мнимой осью.

Если частота внешнего воздействия соответствует частоте возможных автоколебаний, то , т.е. режим вынужден­ных колебаний возможен при весьма малой амплитуде внешних воз­действий. Поскольку годограф уменьшается при увеличении , то при достаточно высоких частотах внешнего воздействия критическое значение амплитуды становится малым и, сле­довательно, может быть выбрана и малая амплитуда внешнего воз­действия, чтобы сорвать автоколебания и установить режим вынуж­денных колебаний частоты .

9.8 Линеаризация релейных систем

Из-за существенно нелинейных свойств релейного элемента нарушается линейная связь между входной и выходной величинами, однако это позволяет коммутировать большие мощности простыми средствами. Указанный недостаток может быть устранен линеариза­цией релейных систем, которую можно провести несколькими спосо­бами.

1. Линеаризация вынужденными колебаниями. Идея ее заключается в том, что на вход релейного элемента подается, кроме основного, медленно изменяющегося сигнала, высокочастотный сигнал, ампли­туда которого больше амплитуды основного. Если на выходе релей­ного элемента включить фильтр низких частот, то на выходе фильт­ра получим среднее значение, зависящее от величины основного входного сигнала. При малых значениях отношения основного сигна­ла к амплитуде дополнительного гармонического сигнала получает­ся линейная зависимость между входной и выходной величинами ре­лейного элемента.

Неудобство такого метода линеаризации заключается в необхо­димости наличия отдельного независимого генератора, хотя это придает ей гибкость и позволяет изменять амплитуду и частоту до­полнительного периодического воздействия.

2. Линеаризация автоколебаниями. В этом случае источником дополнительного периодического воздействия, производящего линеа­ризацию, являются автоколебания самой релейной системы, если частота их намного выше частоты внешнего воздействия.

В этих случаях обычно стремятся повысить частоту автоколе­баний введением в управляющий сигнал производной от отклонения, упругих внутренних обратных связей, и т.д. Такая линеаризация релейных систем называется вибрационной. Она не позволяет в желаемом диапазоне изменять частоту и амплитуду автоколебаний.

3. Линеаризация с помощью скользящего режима. Смысл сколь­зящего режима выясним, рассмотрев простейший пример следящей системы, изображенной на рисунке 9.16.

Релейный элемент РП имеет зону нечувствительности и гис­терезис, рисунок 9.10.г. При перемещении движка задающего потенцио­метра увеличивается напряжение, приложенное к РП.

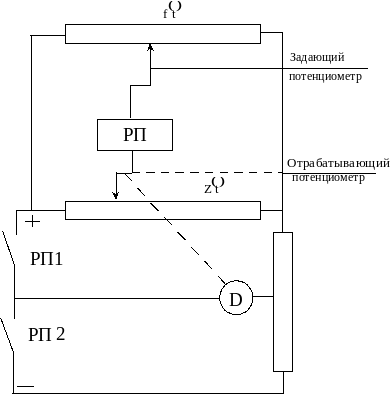
Рисунок 9.16 - Схема иллюстрации скользящего режима

При дости­жении этим напряжением значения релейный элемент срабаты­вает и включает замыкающим контактом или двигатель , который перемещает движок отрабатывающего потенциометра. Как только движок отрабатывающего потенциометра приблизится к поло­жения задающего настолько, что напряжение на реле РП станет равным напряжению отпускания , реле РП отключится, и двигатель остановится.

При дальнейшем изменении положения задающего потенциометра работа системы повторяется. Таким стразом, движок отрабатываю­щего потенциометра будет следить за положением задающего с по­грешностью, равной .

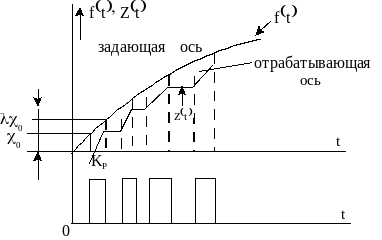
Рисунок 9.17 - График перемещений задающей и отрабатывающей оси

Если характеристики РП представляет собой характеристику идеального релейного элемента (рисунок 9.1,б), то частота включений релейного элемента будет стремиться к бесконечности, при этом движок отрабатывающего потенциометра точно следит за по­ложением движка задающего потенциометра .

Под скользящим режимом понимается режим работы системы, при котором регулирующий орган в процессе компенсации возмущения перемещается кратковременными включениями в одном направлении. При этом очевидно, что средняя его скорость перемещения всегда будет меньше скорости при длительном включении

,

где - постоянная времени сервомотора.

Скользящий режим не может возникнуть в системе с двухпозиционным релейным элементом, поскольку в таком случае происхо­дит реверсирование сервомотора. Скользящий режим, наблюдаемый в релейной системе, линеаризует ее и позволяет применять к ней общие методы исследования линейных систем. В обычной релейной системе при (рисунок 9.18,а) , , однако переключение не изменяет знака производной, хотя в общем случае

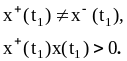(9.66)

Однако в системе возможен другой случай (рисунок 9.18,б), когда

. (9.67)

Этот случай соответствует возникновению скользящего режима. Условием возникновения такого режима, очевидно, является то, что скорость роста сигнала обратной связи больше скорости роста входного внешнего воздействия, что и приводит к отключению релейного элемента.

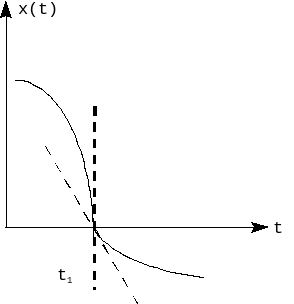
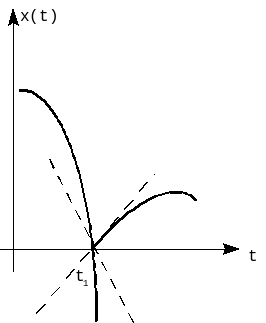
Рисунок 9.18 - Изменение сигнала на входе реле при отсутствии и наличии скользящего режима

Выходной сигнал , будет иметь , если индекс переда-точной функции элемента обратной связи, охватывающего релейный элемент равен единице, рисунок 9.19.

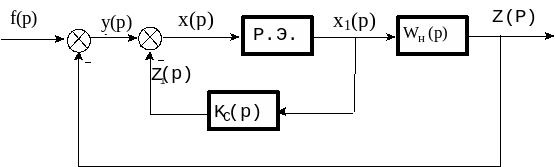
Рисунок 9.19 - Схема реализации скользящего режима

При в релейной системе наблюдается идеальный скользящий режим,при этом

. (10.68)

На основании выражения (10.68) для системы, изображенной на рисунке 9.19, можно записать:

, откуда

, или

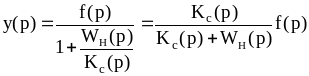. (9.69)

Выражению (9.69) соответствует линейная система, изображенная на рисунке 9.20.

Рисунок 9.20 - Структурная схема линеаризованной системы

Такой же будет схема, у которой вместо релейного элемента установлен усилитель с бесконечным коэффициентом усиления,

.

При

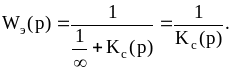
Здесь есть результирующая передаточная функция релейного элемента, охваченного обратной связью.

Таким образом, система, линеаризованная скользящим режимом, совпадает с предельной системой, получаемой при исследовании устойчивости положения равновесия релейной системы в малом.

Для скользящего режима индекс , или прос­то , всегда должен быть равен единице.

Если последовательно с релейным элементом включено звено, охватываемое обратной связью, то индекс произведения передаточ­ных функций этого звена и звена обратной связи должен быть ра­вен единице. В этом случае изменение параметров передаточной функции, последовательно включенной с релейным элементом, не будут сказываться на работе CAP, и, кроме того, в релейной си­стеме наблюдается скользящий режим.

Итак, если релейная автоматическая система устойчива в целом (или малом), и индекс передаточной функции линейной час­ти равен единице, то, начиная с некоторого момента, в релейной системе наступит скользящий режим, который называется частично скользящим режимом.

Непрерывный скользящий режим будет в том случае, если в любой момент времени

. (9.70)

Для выявления скользящего режима необходимо в явном виде найти и , причем находят в предположении , а определяют как реакцию звена обрат­ной связи на ступенчатое воздействие с выхода релейного элемента.

9.9 Метод гармонической линеаризации

Этот метод является приближенным и основан на работах Н.М.Крылова и Н.И.Боголюбова. Впервые он был представлен Е.П.Поповым на II Всесоюзном совещании по теории автоматического регули­рования в 1953 году. Метод отличается простотой, универсально­стью и применим к различным видам нелинейности, позволяет исследовать системы любого порядка с несколькими нелинейностями.

Область использования метода гармонической линеаризации ограничена системами, обладающими высокими фильтрующими свойст­вами и тем точнее, чем выше эти фильтрую­щие свойства.

Метод гармонической линеаризации позволяет опреде-лить условия устойчивости, амплитуду и частоту автоколе-баний, выбрать параметры коректирующих звеньев, обеспечи-вающие заданные характеристики системы.

Входная и выходная величина нелинейного элемента связаны нелинейной зависимостью .

Предполагают и изменяются по гармоническому звкону; выходная величина не зависит от производной и интегра-лов входной величины; среднее значение за период равно нулю

.

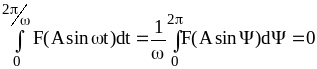Линеаризация нелинейной характеристики нелинейного элемента может быть произведена различными способами, например разложением в ряд Тейлора в окрестности рабочей точки

где

Если на вход нелинейного звена подаются прямоугольные импульсы, то на выходе наблюдаются тоже прямоугольные импульсы причем

Величина в этом случае не остается постоянной, а зависит от - амплитуды входного сигнала.

Если на вход нелинейного звена подан синусоидальный сигнал то на выходе получим

(9.71)

если ограничится в разложении Фурье функции первой гармоникой.

Если учесть, что

, ;

, ;

, ;

, ;

, ;

, четно,

то легко найти коффициенты разложения

Обозначим , тогда

(9.72)

Коэффициент можно записать в таком виде:

или,

изменив пределы интегрирования, 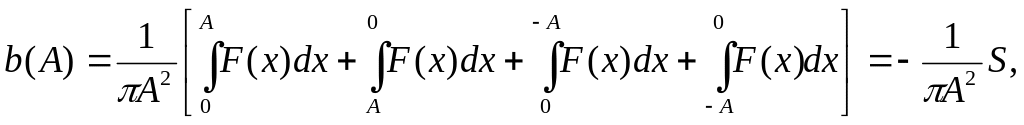(9.73)

где -значение площади петли, образуемой характеристикой нелинейлого элемента, рисунок 9.21. Из этого же рисунка очевидно, что для однозначных характеристик .

Таким образом, для однозначной нечетносимметричной характеристики гармонически линеаризованную связь выходной и входной величин можно представить в виде

. (9.74)

Для нечетносимметричной неоднозначной характеристики

или в операторном виде

С учетом сказанного из выражения (9.71) получаем:

(9.75)

Выражения (9.74) и (9.75) являются приближенными уравнениями нелинейных звеньев. В приложениях даются характеристики неленейностей и их коэффициенты гармонических линеаризаций.

Иногда пользуются понятием эквивалентной переда-точной функции (эквивалентный комплесный коэффициент усиления)

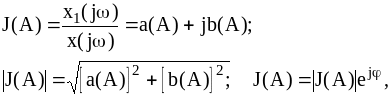(9.76)

где

Нелинейное отставание по координате в виде гистерезисной петли превращается при гармонической линеаризации в эквивалентное линейное отставание по фазе.

Рассмотрим способ вычисления коэффициентов гармони-ческой линеаризации для наиболее часто встречающихся видов нелинейностей (релейных характеристик) (рисунок 9.1 а,б,в,г,д). Наиболее сложный случай представляет релейная характеристика с зоной чувствительности и гистеризисом, изображена на рисунке 9.21.

При симметричных нелинейных характеристиках:

,

а для симметричных относительно начала координат характеристик получаем

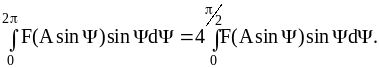
C учетом сказанного рассмотрим характеристику изображенную на рисунке 9.21. Для этого случая

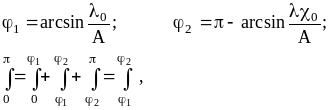
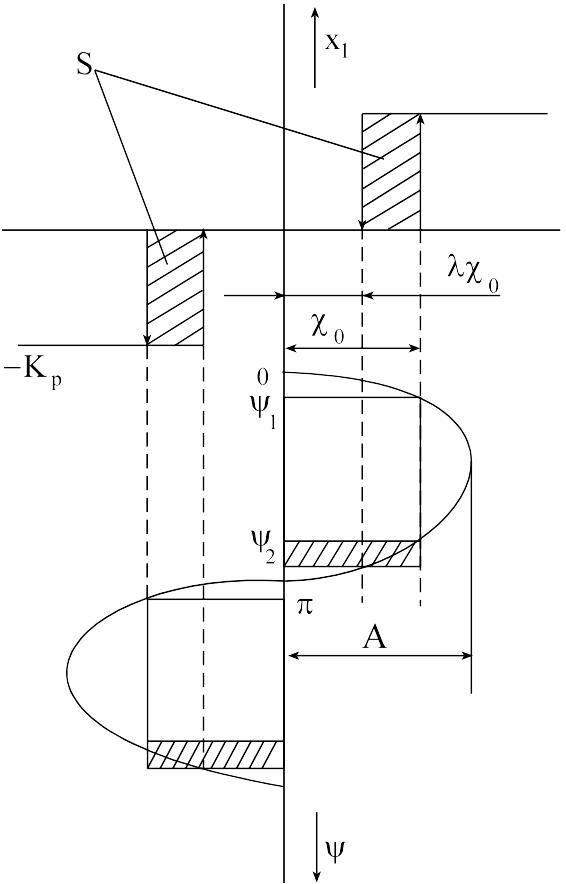
Рисунок 9.21 - Физический смысл коэффициента

поэтому

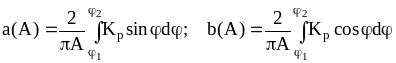. (9.77)

Интегрируя выражения (9.77), находим

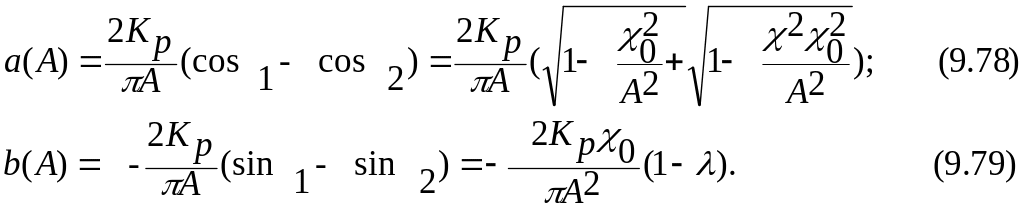
В частном случае, если

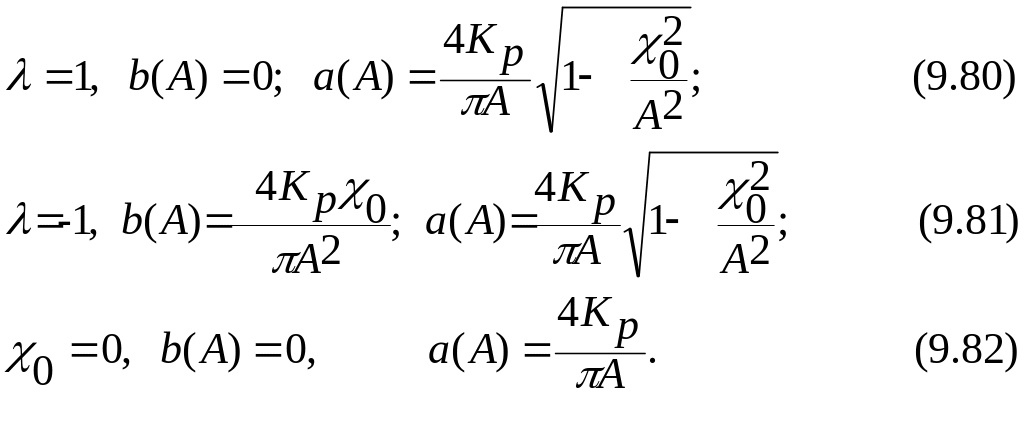
Таким образом, мы получили выражения для коэффициентов гармонической линеаризации для наиболее распространенных видов релейных характеристик.

Уравнение свободных колебаний в нелинейной системе

Для нелинейной системы, состоящей из одного нелинейного элемента и линейной части (рисунок 10.22), составим приближенное уравнение замкнутой системы.

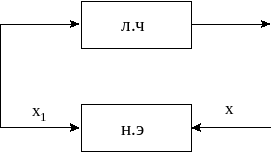
Рисунок 9.22 - Расчетная схема нелинейной системы

Для линейной части

. (9.83)

Для нелинейного элемента

. (9.84)

Передаточная функция разомкнутой системы

. (9.85)

Складывая числитель и знаменатель передаточной функции

разомкнутой системы (10.85) и приравнивая сумму к нулю, полу­чаем условное характеристическое уравнение замкнутой линеаризованной системы

. (9.86)

Если в системе регулирования возникают свободные незату­хающие колебания постоянной амплитуды и частоты

, то коэффициенты характеристического уравнения становятся постоянными. В этом - условность характеристического уравнения (9.86), поскольку , входящее в уравнение, является пара­метром системы, а не частотой, задаваемой извне.

Если решение характеристического уравнения (9.86) при дает вещественные положительные значения и , то в системе возможны автоколебания с полученной амплитудой и час­тотой. Это соответствует появлению незатухающих колебаний в ли­нейной системе, что говорит о наличии чисто мнимых корней ха­рактеристического уравнения. Поэтому появление незатухающих свободных колебаний в нелинейной системе может быть обнаружено с помощью методов отыскания границы устойчивости линейной сис­темы.

Способы определения автоколебательных режимов в нелинейной системе

а) Метод Гольдфарба

Условие возникновения незатухающих колебаний в системе, рисунок 9.22,

,

или

. (9.87)

Решение может быть получено графически, если на комплекс­ной плоскости изобразить и . Если указанные характеристики пересекаются, то решение существует, и в системе возможны автоколебания с частотой, соответствующей частоте точки пересечения характеристик. Если и не пересекаются, то в системе не могут существовать колебания ко­нечной амплитуды.

Изменяя амплитудно-фазовую характеристику линейной части системы , можно избежать возникновения автоколебаний и сделать систему устойчивой.

В том случае, когда и пересекаются, возникает вопрос, а будут ли автоколебания устойчивыми?

Для ответа на этот вопрос рассмотрим рисунок 9.23. Пусть амплиту­да колебаний в точке возросла и равна Тогда точка переместится из в точку и будет соответство­вать . Общий коэффициент усиления разомкнутой системы равен .

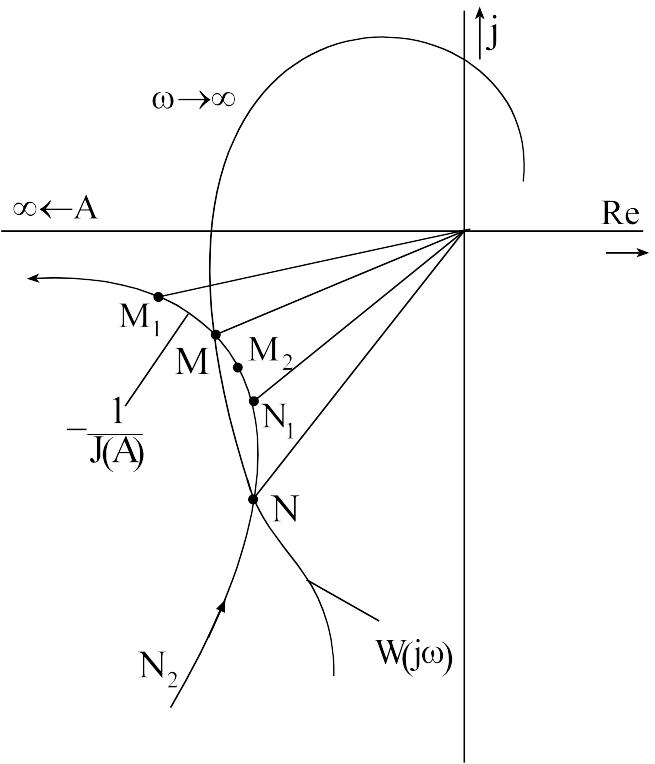
Рисунок 9.23 - Иллюстрация метода Гольдфарба.

Согласно критерию устойчивости Найквиста-Михайлова система ре­гулирования будет устойчива, если не схватывает точ­ку , или, если не охватывает точку конца вектора , т.е. . В рассматриваемом случае охватывает точку , и, следовательно, амплитуда колебаний будет возрастать.

Если амплитуда колебаний уменьшается, то вектору будет соответствовать точка . Вектор не охватывает ее и, следовательно, амплитуда колебаний умень­шается дальше, система будет устойчива, автоколебания с часто­той, соответствующей точке , будет неустойчивы.

Пусть в системе есть автоколебания, соответствующие точ­ке . При увеличении амплитуды значение сместится в точку . При этом не будет охваты­вать точку , следовательно, система устойчива, автоколеба­ния уменьшатся по амплитуде, и точка переместится в точку . Если амплитуда автоколебаний уменьшится по сравнению с амплитудой, соответствующей точке , то (здесь: ) сместится в точку . При этом будет охватывать точ­ку , система станет неустойчивой, и амплитуда колебаний начнет возрастать, смещая точку к .

Таким образом, точке соответствует наличие в системе устойчивых автоколебаний.

Анализ рассмотренных случаев показывает, что автоколеба­ния в нелинейной системе будут устойчивы, если характеристика пересекает и выходит из зоны охвата при увеличении . Если заходит в зону охвата при увеличении , то автоколебания в системе неус­тойчивы.

Аналитический метод

В общем случае нелинейный элемент может иметь характеристику

. (9.88)

Для неоднозначной нелинейности, когда выполняется условие (10.88), коэффициенты гармонической линеаризации " " и " " зависят как от , так и от . Подставив в характеристическое уравнение (10.86) , получим

или

, (9.89)

где и - вещественная и мнимая часть характе­ристического уравнения.

Приравняв отдельно нулю вещественную и мнимую часть, полу­чим два уравнения с двумя неизвестными .

. (9.90)

Полученные совместным решением системы (9.90) значения и  должны быть вещественными положительными. Только в этом случае имеет смысл проверять их на устойчивость. На рисунок 9.24 построена серия годографов типа Михайлова в плоскости координат , .

Устойчивой системе соответствует охват начала координат

годографом.

Пусть годограф проходит через начало координат. Дадим при­ращение амплитуде колебаний . Этому будет соответствовать смещение годографа относительно начала координат, оце­ниваемое вектором. .

Рисунок 9.24 - Годографы типа Михайлова

Изменению >0 будет соответствовать вектор .

Если, , то годограф типа Михайлова будет охваты­вать начало координат. Но , поэтому

автоко­лебания будут устойчивы, если

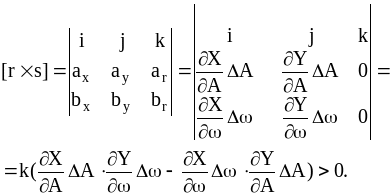
Это будет иметь место, если выполняется условие:

, (9.91)

поскольку .

Система управления будет устойчива, если выполняется не­равенство (9.91).

Частные производные (9.91) берутся в точке ; =₀. Для систем, описываемых дифференциальным урав­нением 5-го порядка и выше, необходимо проверить выполнение критерия устойчивости Михайлова для остальной части годографа.

Использование определителя Гурвица

Условием наличия в характеристическом уравнении пары мнимых корней является равенство нулю предпоследнего определителя Гурвица .Все остальные определители должны быть положительными.

Этот способ имеет практический смысл лишь в том случае, если коэффициенты характеристического уравнения не зависят от , т.е. когда нелинейность однозначна.

Приравнивая нулю предпоследний определитель, находят зна­чение амплитуды автоколебаний. Для отыскания частоты автоколе­баний можно воспользоваться одним из уравнений (9.90), в кото­рых амплитуда колебаний будет уже известной величиной.

Автоколебания в системе устойчивы, если при увеличении амплитуды колебаний выше расчетного значения будет по­ложительным, а при уменьшении - отрицательным. Иными словами, нелинейная система имеет устойчивые автоколебания, если

. (9.92)

Использование годографа типа кривой Михайлова

Этот метод нахождения параметров автоколебаний использует­ся тогда, когда другие методы оказываются слишком громоздкими.

Рассматривая как прямоугольные коорди­наты, строят на комплексной плоскости кривые для серии конкрет­ных значений и . Амплитуда и частота автоколебаний опре­деляются параметрами той кривой, которая проходит через начало координат, рисунок 9.24.

Задаваясь различными значениями , строят серию кри­вых при изменении  в диапазоне, соответствующем их располо­жению у начала координат.

Если нет значений , при которых кривая типа Михайлова проходит через начало координат, то автоколебания в системе отсутствуют.

Устойчивость автоколебаний может быть проверена по значе­ниям для различных кривых. Если для случая, изображенного на рисунке 9.24 , то автоколебания устойчивы, поскольку для кривая типа Михайлова соответствует устойчивой сис­теме. При этом амплитуда колебаний будет уменьшаться и при в системе возникнут незатухающие автоколебания. Для система неустойчива, амплитуда колебаний в системе будет возрастать, и при наступит состояние устойчивого периодического движения с частотой .

9.10 Метод фазовой плоскости

Исследование нелинейных систем сопряжено со значительны­ми трудностями, потому что не существует единого точного мето­да решения нелинейных уравнений. Для каждого вида нелинейности приходится изыскивать специфический частный метод.

Существенный интерес в теории управления представляет собой класс систем, состоящих из ряда линейных элементов и одного нелинейного.

Метод изображения переходных процессов на фазовой плоскости был введен академиком А.А.Андроновым. Метод дает воз­можность получить наглядную и точную картину всей совокупности переходных процессов при любых начальных условиях для систем второго порядка, содержащих нелинейные элементы.

Фазовой плоскостью называется плоскость, в которой по осям координат откладываются какие-либо две переменные, харак­теризующие переходный процесс в системе. Наиболее часто в ка­честве таких координат используются отклонения регулируемой ве­личины и скорость ее изменения. Нелинейное дифференциальное уравнение вида

(9.93)

сводится к двум дифференциальном уравнениям первого порядка введением переменной .

, . (9.94)

Эта система уравнений является частным случаем более обще­го

, (9.95)

где и - нелинейные функции координат.

Для изображения переходного процесса на фазовой плоскости исключим из этих уравнений время. Для этого разделим второе на первое.

. (9.96)

В итоге получили нелинейное дифференциальное уравнение, у кото­рого нет общего решения, поэтому всякий раз приходится изыскивать частный метод его решения. Решение уравнения (9.96) есть некоторая функция , графическое изображение которой на фазовой плоскости называется фазовой траекторией. Каждой точке фазовой плоскости соответствует только одна фазовая траектория, кроме особых точек. Это позволяет для различных начальных ус­ловий и получить наглядные фазовые портреты. Особыми точками называются такие, в которых происходит одновременное обращение в нуль функций и :

. (9.97)

На основании выражения (9.97) в особых точках и обра­щаются в нуль, т.е. движение в них прекращается, они представляют собой точки равновесия системы. Это могут быть реали­зуемые особые точки, т.е. устойчивые, или нереализуемые, существующие формально.

Если координата , т.е. дана система уравнений (9.94), тогда фазовые траектории приобретают некоторые дополни­тельные свойства.

1. В верхней полуплоскости , поэтому при возрастании координата увеличивается и, следовательно, движение происходит на фазовой плоскости слева направо. В нижней полу - плоскости , движение происходит справа на налево.

2. Если второе управление (9.94) разделить на первое, то

.

При , т.е. в точках пересечения фазовых траекторий с осью касательные к фазовым траекториям перпендикулярны оси .

Фазовые траектории линейного звена второго порядка

На примере построения фазовых траекторий линейного звена второго порядка легко проследить получение фазовых траекторий и особых точек наиболее важных типов, встречаемых в нелинейных системах. Пусть уравнение свободных колебаний в системе пред­ставимо в виде

или

. (9.98)

Геометрическое место точек, в которых наклон касательных ко всем фазовым траекториям одинаков, представляет собой линии, называемые изоклинами. В рассматриваемом случае изоклины прямолинейны

, (9.99)

где - угловой коэффициент касательной к траектории. Пря­мая линия проходит через начало координат. Угловой коэффициент изоклины равен

.

Из (10.99) следует, что при ,

при .

1. Если , то все траектории пересекают ось у под от­рицательным углом тем большим, чем больше коэффициент демпфиро­вания . Если , то траектории будут пересекать ось у под прямым углом. Биссектрисы квадратных углов имеют , экстремумам фазовых траекторий соответству­ет .

Вид фазовой траектории зависит от корней характеристического уравнения

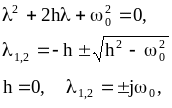, (9.100)

где ₀ - частота собственных колебаний идеального осцилятора без демпфирования.

Из системы уравнений (9.98)

. (9.101)

Решив это уравнение, получаем уравнения фазовой траектории.

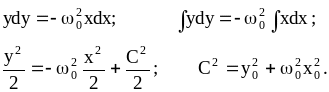
Произвольная постоянная определяется из условия ,

. В итоге получаем уравнение эллипса

,

где ,

и - оси эллипса, , (рисунок 9.25).

Для получаем уравнение , эллипсы превращаются в концентрические окружности.

Начало координат в данном случае не принадлежит ни одной из траекторий и называется особой точкой типа центр.

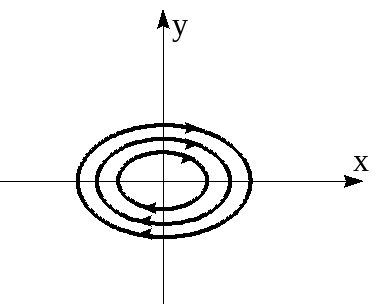
Рисунок 9.25 - Фазовые траектории, соответствующие особой точке типа центр

Для всякой заданной области, включающей центр, можно найти такие начальные условия и , при которых замкнутая кривая не будет выходить из заданной области. Это значит, что равновесие в точке (0,0) будет устойчивым в смысле Ляпунова, но асимптотической устойчивостью точка типа центр не обладает.

2. .Уравнение фазовой траектории принимает вид:

. (9.102)

Корни характеристического уравнения (9.100)- комплексно сопряженные, т.е.

(9.103)

Можно доказать, что логарифмические спирали с уравнением в полярной системе координат соответствуют системе (9.103).

Если , то при и стремятся к нулю, рисунок 9.26,а,б. Начало координат - это особая точка, которая в данном случае называется фокусом. Все траектории стягиваются к началу координат (или уходят).

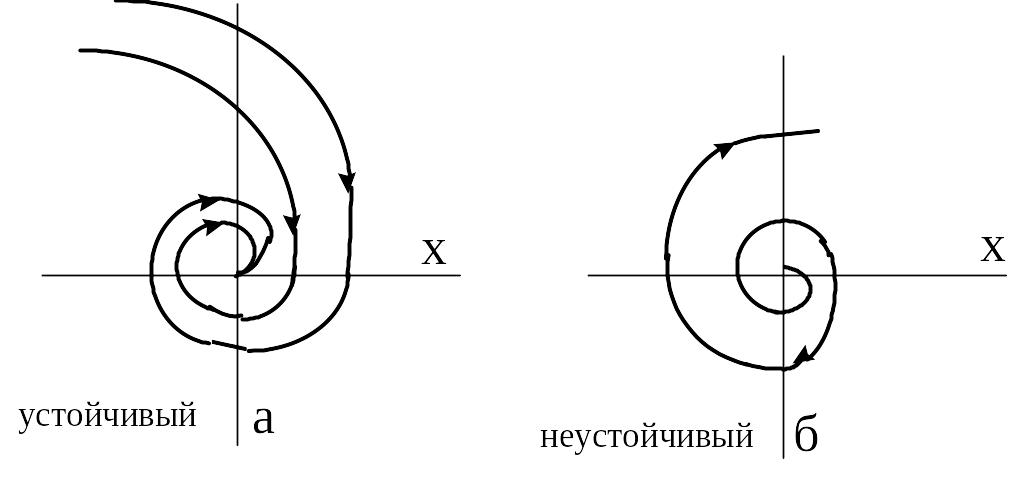
Рисунок 9.26 - Фазовые траектории, соответствующие особой точке типа фокус

3. . Рассмотрим вначале положительное демпфирование . Можно доказать, что существует два прямых луча, проходящих через начало координат, которые одновременно являются фазовыми траекториями.

Пусть уравнение искомого луча .

Подставляя это выражение в уравнение (10.99), получаем

.

Получили уравнение такое же, как и исходное характеристическое уравнение (9.100). Угловой коэффициент является корнем характеристического уравнения исходного зве-на. Это говорит о том, что, во-первых, такой луч существует и, во-вторых, таких лучей два, рисунок 9.27.

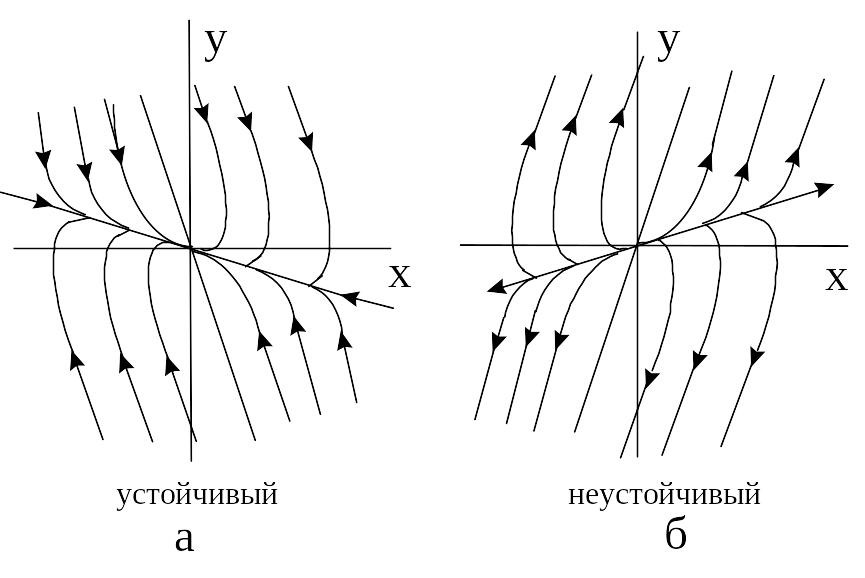
Рисунок 9.27 - Фазовые траектории, соответствующие особой точке типа узел

Луч, ближайший к оси ординат совпадает с одной из траекторий. Другой луч представляет собой предельную траекторию, к которой стремятся все остальные фазовые траектории. Внутри угла, образованного лучами, траектории идут монотонно, приближаясь к началу ординат, т.е. область внутри луча представляет собой область начальных условий, при которых процесс будет монотонным. За пределами этого луча переходный процесс будет не монотонен и с перерегулированием. Устойчивый процесс, когда корни вещественные отрицательные, приведен на рисунке 9.27,а, неустойчивый переходный процесс (корни положительные) - на рисунке 9.27,б.

Все траектории, стягиваясь к началу координат, имеют в точке равновесия одинаковые касательные и с вполне определен­ным наклоном. Такая точка равновесия называется устойчивым узлом (неустойчивым узлом).

4. Случай с отрицательной упругой силой. Уравнение динами­ки в этом случае принимает вид

. (9.104)

Существуют два луча с угловыми коэффициентами

,

которые разделяют фазовую плоскость на четыре характерные об­ласти, в каждой из которых фазовые траектории имеют гиперболи­ческий характер. Лучи, являясь асимптотами гипербол, представ­ляют собой особые траектории.

От луча, проходящего во втором и четвертом квадрантах ги­перболы удаляются, к лучу в первом и третьем квадрантах они приближаются асимптотически.

Наклон лучей зависит от . При он становится равным , и фазовые траектории располагаются симметрично относительно осей координат, рисунок 9.28.

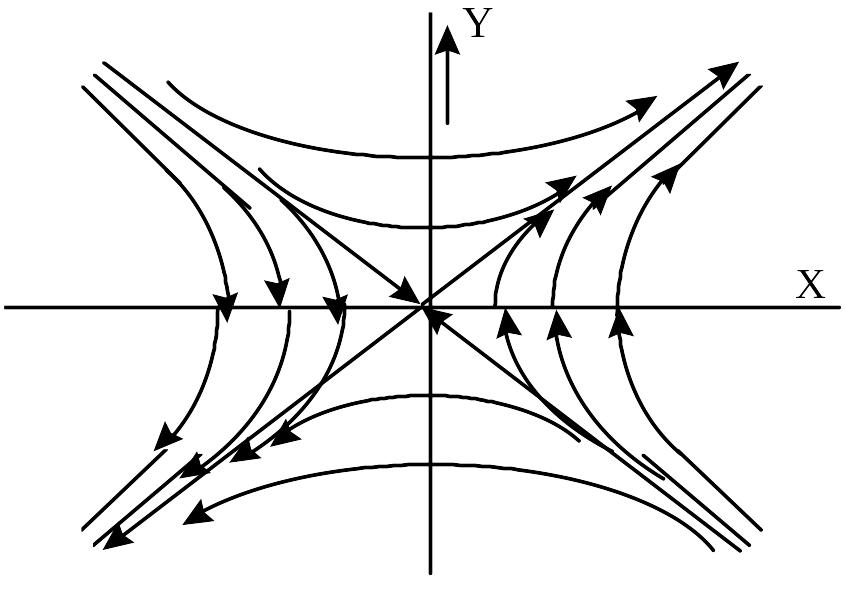
Рисунок 9.28 - Фазовые траектории, соответствующие особой точке типа седло

Особая точка - начало координат - является неустойчивой особой точкой. Фазовые траектории сначала приближаются к ней, а затем начинают удаляться. Такая особая точка называется сед­лом.

Если интегрирование дифференциальных уравнений фазовых траекторий затруднено или невозможно, фазовый портрет может быть построен графоаналитическим или графическим методом. Од­ним из таких методов является метод изоклин. Чтобы получить уравнение изоклины, необходимо в дифференциальном уравнении фазовой траектории положить .

При этом уравнении изоклины

, (9.105)

где - есть тангенс угла наклона фазовой траектории к оси абсцисс. Задаваясь различными значениями , получим семей­ство кривых, изоклин, рисунок 9.29.

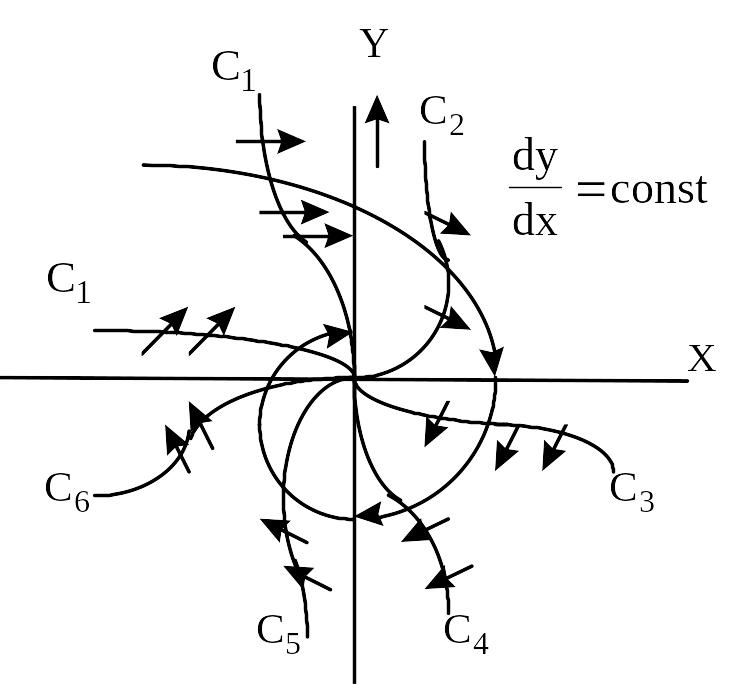
Рисунок 9.29 - Построение фазовых траекторий методом изоклины

В первом приближении фазовая траектория может быть построе­на по стрелкам на изоклинах, указывающим наклон фазовых траек­торий в точках, образующих изоклин

Более точно фазовую траекторию можно построить, если использовать метод канонических полигонов, заключающийся в том, что, если известны направления касательных к интегральной кри­вой на соседних изоклинах, то угол наклона траектории кривой выбирается как биссектриса угла, образованного этими направлениями на предыдущей изоклине, рисунок 9.30

Метод изоклин достаточно громоздок и трудоемок, его точность определяется числом изоклин и (при желании) может быть достаточно высокой, если выбрать соответствующее число изоклин и масштаб чертежа.

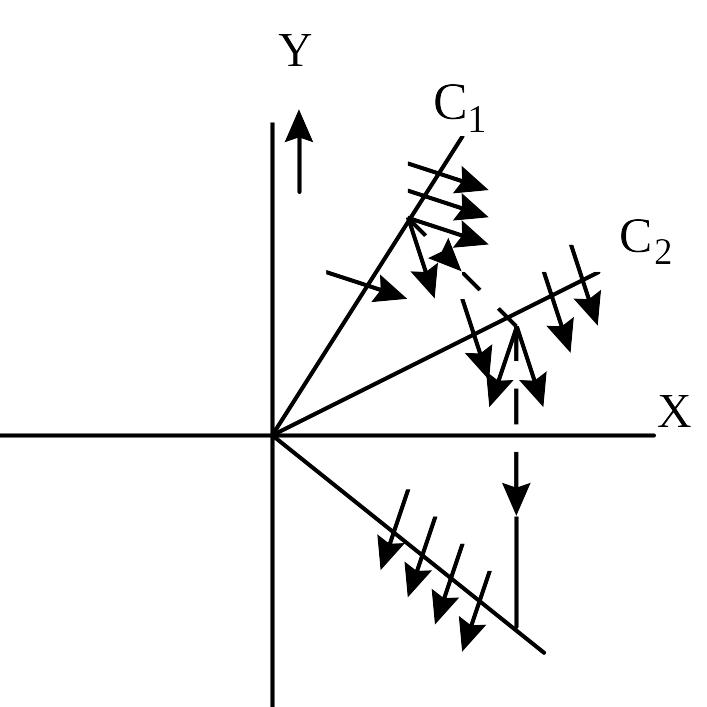
Рисунок 9.30 - Иллюстрация метода канонических полиномов

Метод точечных преобразований

Применение метода фазовых портретов для многомерных авто­матических систем становится затруднительным, особенно в слу­чае медленно затухающих или автоколебательных систем вследст­вие возрастающей трудоемкости графических построений. Поэтому актуальна разработка метода, позволяющего без построения пол­ного фазового портрета определять характер колебаний, наличие автоколебаний и их характеристик в системе. Эту задачу решил академик А.А.Андронов с помощью метода точечных преобразований.

Практически рассматриваемый метод получил распространение лишь для систем второго порядка, описываемых кусочно-линейными уравнениями.

Сущность его состоит в том, что фазовая плоскость разбива­ется на ряд областей, в пределах которых переходные процессы описываются линейными дифференциальными уравнениями.

При переходе их из одной области в другую уравнения тоже изменяются скачком к новой форме. С помощью этих уравнений ана­литически определяются положения начальных и конечных точек фа­зовых траекторий на стыках областей (линии переключения). По расположению граничных точек фазовых траекторий можно судить о характере колебательных движений, о наличии предельных циклов и т.д.

Пусть известны уравнения линий переключения (пунктирные линии) и уравнения фазовых траекторий в первой и второй облас­тях, рисунок 9.31.

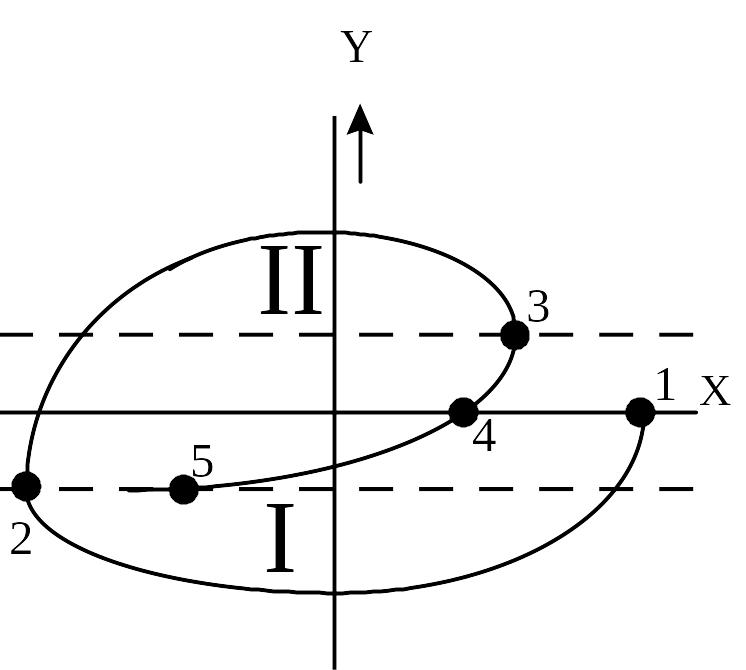
Рисунок 9.31 - Иллюстрация к методу точечных преобразований

Выбрав начальную точку 1, с помощью уравнений линии пере­ключения и фазовой траектории в первой области находим точку 2. Аналогично находим точки 3 и 5. В итоге получаем точечное пре­образование правой полуоси X самой в себя. Достаточно вычис­лить точки 2,3,4,5 не строя фазового портрета.

Точка 4 лежит ближе к началу координат, чем 1, следователь­но, колебания затухают. Задаваясь различными начальными усло­виями в пределах возможных, можно построить характеристику за­висимости , которая называется функцией последования, рисунок 9.32.

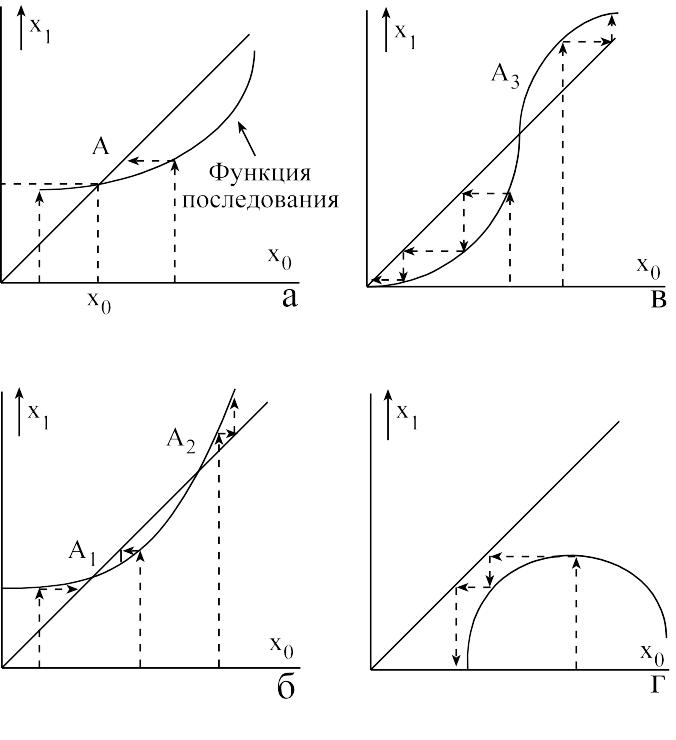
Рисунок 9.32 - Виды функций последования

Если провести линию под углом в 45°, то получим точку пересечения с функцией последования. В этой точке , т.е. точка преобразуется сама в себя, что соответствует предельному циклу. Произведя простые построения, легко определить характер автоколебаний. Эти построения носят название диаграм­мы Ламерея, рисунок 9.32,б,в,г. На рисунке 9.32,6 точке соответствуют устойчивые автоколебания и, следовательно, устойчивый предельный цикл, а точка - неустойчивый предельный цикл. Точке на рисунке 9.32. в соответствует неустойчивый предель­ный цикл. Для функции последования, изображенной на рисунке 9.32.г предельные циклы отсутствуют, автоколебаний в системе тоже нет.

Особенности метода точечных преобразований

1. Применим только для кусочно-линейных систем, так как только для них возможно аналитическое вычисление положения граничных точек.

2. Необходимо знание уравнений линий переключения.

3. Полученные характеристики не имеют прямой связи с параметром времени.

В настоящее время разработан обобщенный метод точечных преобразований, используемый для существенно нелинейных и многократных колебательных систем. Он свободен от недостатков классического метода А.А. Андронова (см. А.В. Башарин, И.А. Башарин "Динамика нелинейных автоматических систем управления").

Литература

1 Теория автоматического управления. В част./ Н.А.Бабаков, А.А.Воронова и др. под. ред. А.А.Воронова. - М.: Высшая школа, 1986 г. ч.1 - 367 с .

2 Зайцев Г.Ф. Теория автоматического управления и регулирования. - Киев: Вища школа, 1988 г. - 430 с., ил.

3 Попов Е.П. Теория линейных систем автоматического регулирования и управления. - М.: "Наука", 1978 г. - 256 с.

4 Пугачев В.И. Методические указания и программы расчета основных характеристик систем автоматического управления. Краснодар, Изд. КубГТУ, 1996, - 77с.

5 Теория автоматического управления. В част./ Н. А. Бабаков, А. А. Воронова и др. под. ред. А.А.Воронова. - М.: Высшая школа, 1986 г.

Ч 2 - 504 с., ил.

6 Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. - М.: Наука, 1988 г. - 256 с.

7 Цыпкин Я.З. Релейные автоматические системы. -М.: Наука, 1974, -575 с.

156