6.5 Ошибки сау при типовых режимах работы

Стабилизирующие САУ работают при постоянном значении заданий величины. В программных или следящих системах заданное значение может изменяться по линейному закону. В этом случае точность ас­татической системы будет определяться по установившейся погрешности отработки сигнала постоянной скорости, которая называется ки­нетической погрешностью:

; ; .

. (6.14)

Поскольку система астатическая, то , поэтому необходимо раскрыть неопределенность по правилу Лопиталя:

.

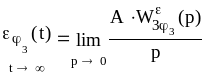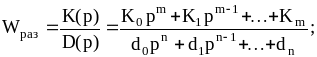если , то

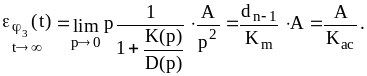(6.15)

Здесь добротность разомкнутой астатической

системы.

Статическая ошибка замкнутой астатической САУ пропорциональна скорости входного сигнала и обратно пропорциональна добротности разомкнутой САУ.

При подаче на вход гармонического сигнала ошибка регулирова­ния определяется через комплексный коэффициент уси­ления САУ по тому или другому воздействию, т.е. через амплитудно-фазовую характеристику.

Возмущающие воздействия САУ должна подавлять (не пропускать), а задающие пропускать без искажений. В системах, предназначен­ных для воспроизведения гармонического сигнала (следящие системы), необходимо, чтобы

. (6.16)

Очевидно, что условие идеального воспроизведения неосуществимо, поэтому можно поставить условие, чтобы в диапазоне частотного спектра воздействия выполнялось неравенство:

, (6.17)

где - допустимая величина амплитудной погрешности, . Отсюда следует, что

.

Для подавления нежелательных гармонических помех необходимо, чтобы

. (6.18)

Поскольку указанное условие может быть выполнено лишь при , что нереально, то необходимо, чтобы в рабочем диапазоне частот возмущений , где -допустимое отношений колебаний выходной величины к амплитуде входного внешнего возмущения.

6.6 Метод коэффициентов ошибок

Точность работы системы при произвольной форме входного сигнала может быть оценена с помощью коэффициентов ошибок, формулу которых записывают в виде:

, (6.19)

где - коэффициенты ошибок в случае возмущающего воздействия. Аналогичное выражение можно записать для случая задающего воздействия. Чем меньше коэффициенты ошибок, тем точнее САУ относительно произвольного входного сигнала (в смысле воспроизведения или подавления).

Пусть (6.20)

Его изображение .

Изображение ошибки

, где (6.21)

Изображение ошибки можно записать так:

(6.22)

где - полином, соответствующий полюсам

Из последнего выражения легко найти коэффициенты и т.д.

Продифференцировав один раз левую и правую части и приравняв , получим .

Поступая и дальше аналогичным образом, для любого коэффициента получаем выражение:

.

Поскольку , где ,

, то

.

Переходя к оригиналам, получаем формулу коэффициентов ошибок по задающему воздействию:

(6.24)

Коэффициенты легко определить, разложив передаточную функцию замкнутой системы по положительным степеням :

Приводя к общему знаменателю и сравнивая коэффициенты при одинаковых степенях , получаем систему уравнений:

,

,

.

Необходимо записать столько уравнений, сколько коэффициентов желают определить. Систему уравнений можно решить по правилу Крамера

,

где - определитель системы, в котором вместо -го столбца стоит столбец свободных членов.

6.7 Структурная неустойчивость САУ

САУ называется структурно неустойчивой, если никаким измене­нием величины параметров (но не их знака или структуры системы) ее нельзя сделать устойчивой. Наиболее существенные исследования в этом вопросе принадлежат М.А.Айзерману (1948 г.) и Гантмахеру Ф.P. (1954 г.). В качестве примера рассмотрим систему, изобра­женную на (рисунке 6.7). Пусть ; ; . В соответствии с правилом определения харак­теристического уравнения замкнутой системы по передаточной функции разомкнутой имеем:

, или

.

Это уравнение не содержит члена с оператором , т.е. не вы­полняется необходимое условие устойчивости - положительность и наличие всех коэффициентов характеристического уравнения.

Пусть теперь система имеет консервативное звено , а два других, соответственно: усилительное

, апериодическое .

Характеристическое уравнение такой замкнутой системы будет:

, или

.

Как видно из характеристического уравнения, все коэффициенты его присутствуют и положительны. По критерию Гурвица условие устойчивости САУ запишем так:

.

Это условие выполнено быть не может при положительных значе­ниях т.е. без изменения знака. Следовательно САУ структурно неустойчива.

Для того, чтобы при проектировании заранее отбросить вариан­ты, соответствующие структурной неустойчивости, необходимо проверить некоторые условия.

Пусть одноконтурная система содержит:

- интегрирующих звеньев,

- неустойчивых звеньев,

- консервативных звеньев.

При отсутствии производных в законе управления (в числителях передаточных функций отсутствуют производные) система будет устойчивой структурно, если , где - степень характеристическом уравнения.

При наличии воздействия по первой производной и при для структурной устойчивости необходимо выполнение следующих усло­вий:

для ,

для ,

для .

Имеются и другие условия структурной устойчивости, учитываю­щие степень числителя и знаменателя передаточной функции разомкнутой системы, число вещественных и нулевых корней знаменателя, число мнимых, ненулевых и комплексных корней знаменателя справа от мнимой оси, которые здесь не приводятся.

6.8 Граница устойчивости и область устойчивости в плоскости одном и двух параметров

Для выделения области параметров, обеспечивающих устойчивую работу САУ, используются критерии устойчивости. Рассмотрим приме­нение каждого из них для выделения области устойчивости по одному и двум параметрам.

Критерий устойчивости Гурвица.

Пусть САУ имеет один параметр настройки . Для выделения об­ласти значений , обеспечивающих устойчивость САУ запишем все условия устойчивости - положительность всех главных диагональных миноров до « » при . В частном случае может входить и в . Равенство нулю миноров соответствует границе устойчивости.

Если построить зависимости , , то значение параметра , удовлетворяющие условию устойчивости, будет лежать на оси абсцисс в той области зна­чений , для которых миноры положительны (рисунок 6.8).

Если САУ имеет два параметра настройки и , то приравняв нулю получим уравнение границы устойчивости в плоскости двух пара­метров. Задаваясь значениями одной из них, по каждому уравнению можно найти значение другого и построить линии границы устойчивости. При этом плоскость параметров и будет разделена на области. Для определения области, удовлетворяющей условию устойчивости, необходимо из каждой области взять одну точку и проверить на устойчивость (рисунок 6.8).

САУ находится на границе устойчивости, если характеристиче­ское уравнение имеет нулевые или мнимые корни.

Выделив вещественную мнимую часть годографа Михайлова и приравняв их к нулю, получим аналитические выражения, которые должны удовлетворяться при одном и том же значении , равном, в частности, нулю:

Следует убедиться в том, что все остальные корни имеют отрицательную вещественную часть, т.е. удовлетворяет условию устойчивости.

Если - параметр, для которого необходимо найти область устойчивости, то, сгруппировав все коэффициенты характеристического уравнения с , представим его в виде:

. (6.26)

Построим на комплексной плоскости кривую при изменении до , которая соответствует границе устой­чивости.

Область устойчивости находится только левее этой кривой, ес­ли двигаться по ней в сторону возрастания . Это условие приводится без доказательства, однако для запоминания удобно представлять границу устойчивости корней характерис­тического уравнения на комплексной плоскости - мнимую ось, область устойчивых корней для которого находится слева. При записи области значений параметра необходимо учесть знак перед .

Для построения области устойчивости в плоскости двух параметров необходимо приравнять нулю вещественную и мнимую часть годографа Михайлова:

. (6.27)

Решая их относительно и , находим, и . Исключив из них , получим искомую границу устойчивости .

Если это сделать не удается, то, задаваясь , находят и и строят кривые в плоскости параметров и . Их может оказаться несколько, поскольку и могут быть неоднозначными функциями. Однако полученные кривые соответст­вуют мнимым корням. Для нахождения границы, соответствующей нулевому корню, необходимо положить . Действительно, нулевой ко­рень может быть только тогда, когда .

Для определения границы, соответствующей бесконечному корню, необходимо положить , так как в

можно разделить все слагаемые на , тогда

. Если , то все слагае­мые , , и т.д. стремятся к нулю. Но в правой части равенства также ноль, следовательно . Предельные линии мож­но получить также из и . Положив и .

Область устойчивости в плоскости двух параметров определяется проверкой одной точки каждой области. Однако эту процедуру можно упростить, если выполнить штриховку кривых по методу Ю.И. Неймарка

(1948 г.). Для этого на каждой кривой, определяющей границу устойчивости, берется точка и находится определитель

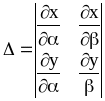. (6.28)

Если он положителен, то штриховку делаю слева, если смотреть в сторону увеличения , и справа, если . Прямые, соответствующие бесконечному и нулевому корню, штрихуются так, чтобы в местах сближения с кривыми их штриховки совпадали (рисунок 6.9). Наиболее вероятным претендентом на область устойчивости является та, которая имеет наибольшее количество штриховок.

Критерий Найквиста - Михайлова.

Возможны два варианта: и принадлежат одному звену; и принадлежат различным звеньям.

В первом случае АФХ разомкнутой системы представляют в таком виде:

.

Граница устойчивости определяется соотношениями:

; .

В нашем случае ;

.

Отсюда

; . (6.29)

Задаваясь , находят и , и . Решая совместно два уравнения с двумя неизвестными, находят точку на кривой границы устойчивости. Линию строят при изменении от до . Определение области устойчивости производится путем проверки одной точки каждой области.

Если и принадлежат различным звеньям, то получают две передаточные функции, в одну из которых входит , в другую .

Уравнения границы устойчивости в этом случае такие:

; . (6.30)

Подставляя конкретные значения , решают совместно систему двух уравнений, в результате которого получают значения и для выбранной частоты, соответствующие одной точке на линии границы устойчивости. Если система уравнений не решается аналитически, используется графоаналитический метод.

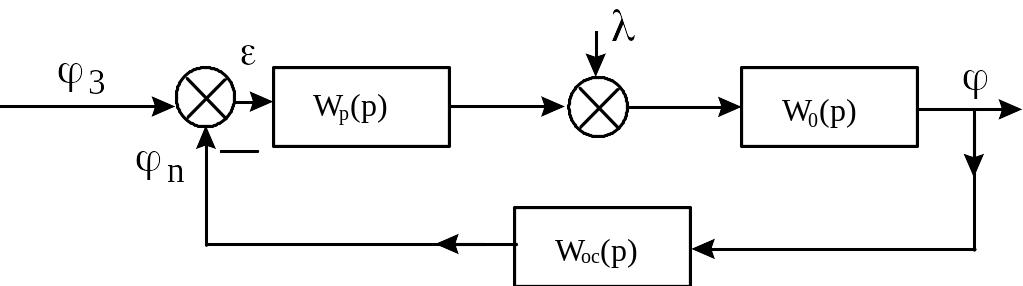
Рисунок 6.8 - Структурная схема системы управления

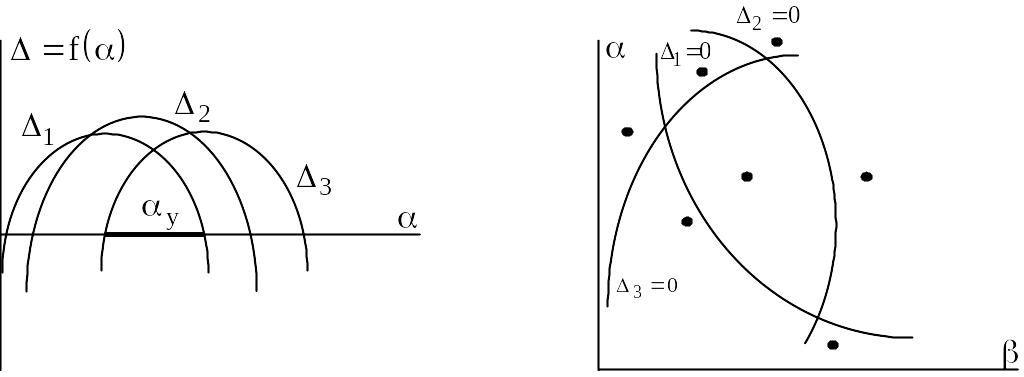
Рисунок 6.9 - Выделение области устойчивости

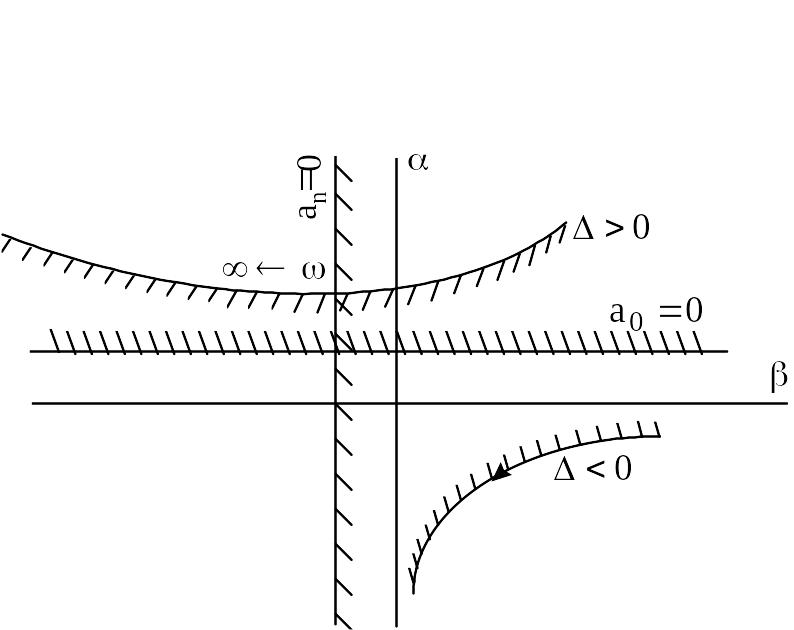
Рисунок 6.10 - Выделение области устойчивости по методу Неймарка

. В выражении (6.30) подставляют значение , в плоскости параметров и строят две кривые, точки пересечения которых будут искомыми решениями.

7 АНАЛИЗ КАЧЕСТВА САУ

Качество регулирования определяется отклонением регулируемой величины от желаемого закона ее изменения в установившемся и переходном режимах. Статические показатели качества характеризуются статической погрешностью. Динамические показатели качества характеризуются временем регулирования, перерегулированием, числом перерегулирований, формой кривой переходного процесса (апериодический, колебательный).

Время регулирования определяется как время от начала переходного процесса до момента, когда выполняется условие:

, (7.1)

где - величина, определяемая требуемой погрешностью работы САУ, обычно .

Перерегулированием называют отношение максимального отклонения регулируемой величины от установившегося значения к величине установившегося значения

. (7.2)

Число перерегулирований определяется по числу максимумов за время регулирования, когда

. (7.3)

Апериодическим называется переходный процесс, при котором регулируемая величина приближается к установившемуся значению без колебаний. Иногда под апериодическим переходным процессом понимают процесс, составляющими которого являются экспоненты, хотя сумма экспонент с различными начальными значениями и постоянными времени может дать несколько колебаний (процесс при отрицательных вещественных корнях характеристического уравнения).

Существуют прямые и косвенные методы оценки качества САУ. Прямые методы предполагают анализ САУ непосредственно путем построения переходного процесса. Косвенные методы позволяют ориентировочно судить о переходном процессе без его построения. К ним относятся: определение степени устойчивости, апериодичности, интегральные критерии качества. Рассмотрим их подробнее.

Критерии апериодичности переходного процесса

Критерий А. М. Каца базируется на вещественности корней характеристического уравнения. Корни характеристического уравнения будут вещественными, если полином удовлетворяет условию устойчивости, где -получается из характеристического уравнения заменой на в производной по от .

Это утверждение легко доказать.

Если в подставить , то получим

.

Если удовлетворяет условию устойчивости, то вещественная и мнимая части , т.е. и имеют вещественные перемежающиеся корни. Но корни вещественны относительно , что равносильно вещественности корней относительно . Поскольку система устойчива, то они отрицательны.

Построив для границу устойчивости, мы тем самым строим границу апериодичности для . Степень в два раза выше степени , поэтому условия апериодичности будут сложнее условий устойчивости.

Критерий Л.Эйлера (1765 г.) позволяет получить условие апериодичности переходного процесса по коэффициентам характеристического уравнения. При этом корни характеристического уравнения могут быть комплексно-сопряженными с отрицательными вещественными частями.

Если характеристическое уравнение записать в форме

,

то для апериодичности переходного процесса необходимо, чтобы для любых смежных коэффициентов выполнялось условие:

, (7.4)

где - степень характеристического уравнения; - индекс проверяемого коэффициента, .

Невыполнение хотя бы одного из неравенств следует считать признаком отсутствия апериодической устойчивости.

Критерий Штурма. Предложен в Парижской Академии в 1826 г. в виде теоремы, из которой вытекает условие апериодичности.

Все корни характеристического уравнения будут отрицательными, если положительны все коэффициенты числом +1 при старших членах ряда Штурма, полученного из этого уравнения, где - его степень.

Ряд Штурма образуется следующим образом:

где - характеристическое уравнение САУ; - производная от по ; - остаток от деления на , взятый с обратным знаком.

Остальные члены ряда получаются таким же образом.

; ;... . (7.5)

При последовательном делении полиномов для образования ряда Штурма можно умножать или делить на какое-либо постоянное положительное число, не зависящее от . Число членов ряда Штурма должно быть +1. Члены ряда должны иметь степень , убывающую на единицу, и последний член должен состоять только из коэффициентов характеристического уравнения.

Недостаток рассмотренных критериев состоит в том, что они не учитывают свойств возмущений, действующих на САУ (не учитывают правую часть дифференциального уравнения).

Для анализа качества систем управления, описываемых дифференциальными уравнениями третьего порядка, И. А. Вышнеградский (1831-1895 гг.) разработал диаграмму, по которой в плоскости двух параметров Вышнеградского можно найти область устойчивости, апериодичности, отсутствия перерегулирования, области равного абсолютного затухания, относительной степени затухания. Однако в связи с частным случаем решенной задачи исследования по данному вопросу не приводятся и могут быть найдены практически в любом учебнике по теории автоматического управления.