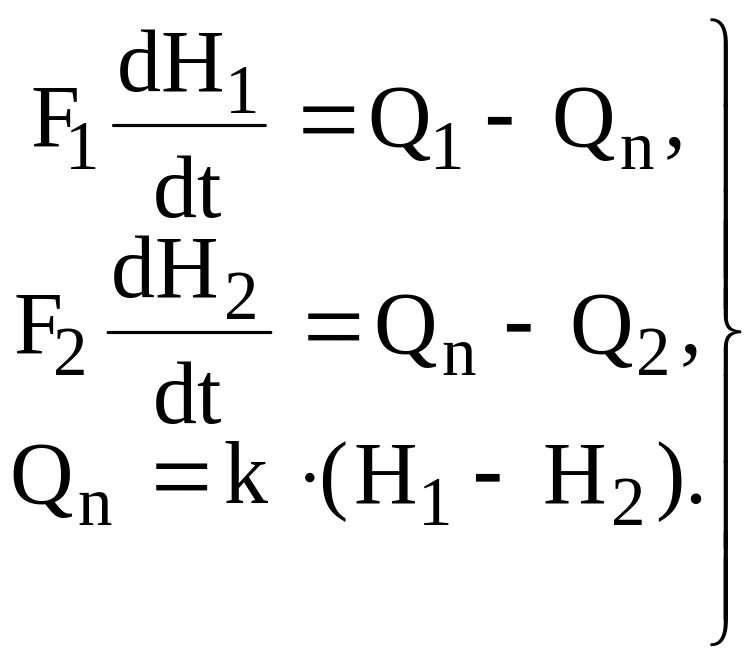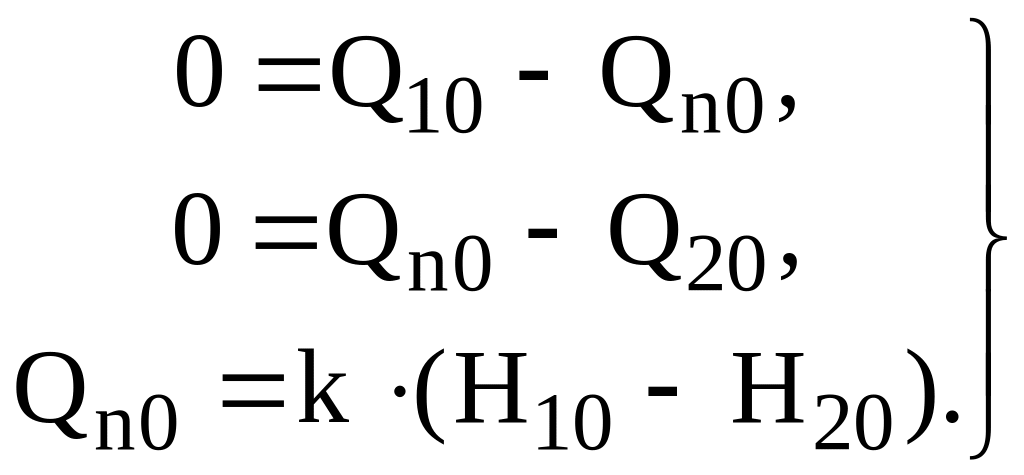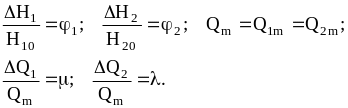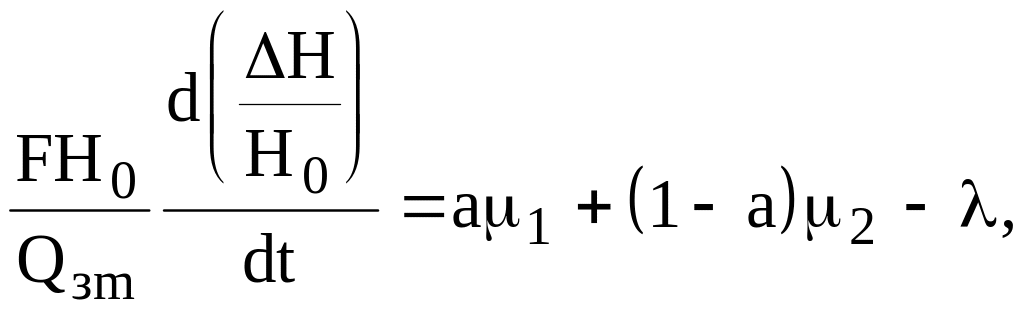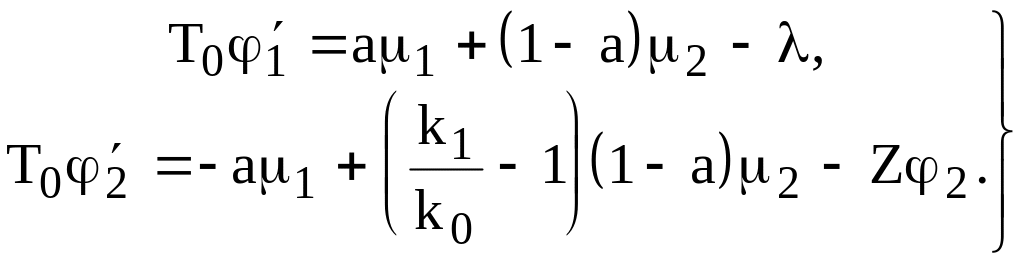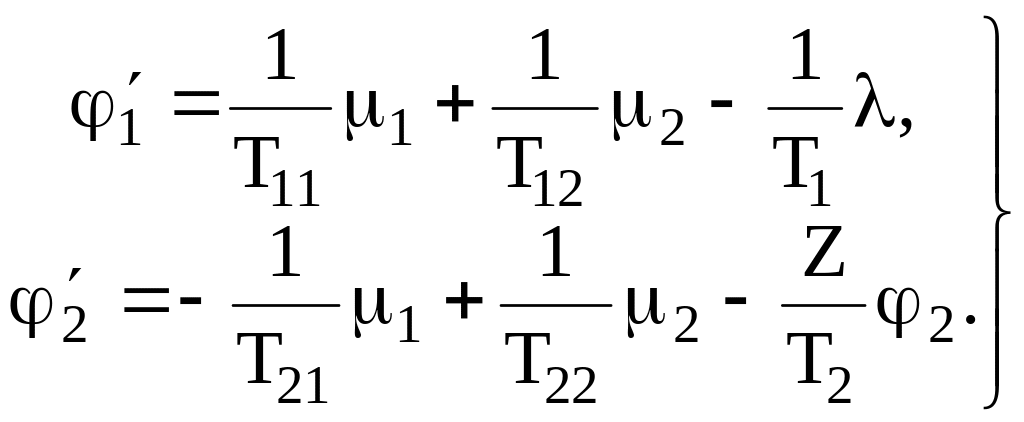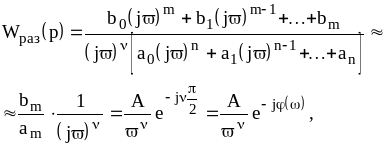Федеральное агенство по образованию

Гоу впо Кубанский государственный технологический университет

(КубГТУ)

Кафедра автоматизации производственных процессов

Факультет Компьютерных технологий и автоматизированных

ванных систем

Пугачев в.И.

ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Конспект лекций по разделам « Линейные непрерывные и нелинейные системы управления » для студентов заочной и МИПС форм обучения специальности

220201- Управление и информатика в технических системах

Краснодар,

Издательство КубГТУ,

2005

Конспект лекций / В.И. Пугачев. Кубан. гос. Техн.Ун-т. Краснодар, 2005.–166 с.

УДК 62-50.007.07

Табл. Ил. 32 Библиогр: 7 назв.

Печатается по решению Редакционно-издательского совета Кубанского государственного технологического университета

Теория автоматического управления, раздел « Линейные непрерывные и нелинейные системы управления»

Приведены сведения из теории линейных непрерывных систем управления. Предназначены для студентов всех форм обучения специальности 220201 - Управление и информатика в технических системах. / Сост. В. И. Пугачев ; Кубан. гос. технол. ун-т. Каф. автоматизации производственных процессов. Краснодар: Изд-во КубГТУ, 2005.-166 с.

Рассмотрены основные понятия и определения, используемые в системах управления, вопросы, связанные с анализом непрерывных линейных и нелинейных систем с целью оценки их работоспособности и возможности синтеза с заданными показателями качества

Рецензенты:

канд.техн.наук, заместитель директора по науке, зав. лабораторией

автоматизации Кубанского филиала

“ ВНИЗ” Ю.Ф. Марков,

канд.техн.наук, профессор КубГТУ

З.Г. Насибов

Кубанский государственный технологический университет , 2005 г.

СОДЕРЖАНИЕ

	Содержание	3
1	Основные понятия теории автоматического упра­вления ..	5
1.1	Введение	5
1.2	Краткая историческая справка развития теории управления	6
1.3	Основные элементы САУ	7
1.4	Классификация САУ	8
1.5	Замкнутые и разомкнутые САУ	10
2	Методика составления уравнений динамики объектов регулирования	13
2.1	Уравнение динамики одноемкостного объекта	13
2.2	Уравнение динамики двухъемкостного объекта	21
2.3	Уравнение динамики объекта с двумя регулируемыми величинами	23
3	Анализ САУ в пространстве состояний	26
3.1	Вектор состояния непрерывной САУ	26
3.2	Переходная матрица состояния	30
4	Основные характеристики простейших звеньев	33
4.1	Типовые входные сигналы	33
4.2	Типовые звенья САУ	36
4.3	Основные законы регулирования	47
5	Устойчивость систем управления	55
5.1	Общие положения об устойчивости	55
5.2	Алгебраический критерий устойчивости Гурвица	57
5.3	Частотный критерий устойчивости Михайлова	58
5.4	Критерий устойчивости Найквиста-Михайлова	62
5.5	Устойчивость САУ с запаздыванием	65
5.6	Логарифмический частотный критерий устойчивости	66
6	Анализ линейных САУ	69
6.1	Структурные преобразования САУ	69
6.2	Связь частотных характеристик и переходных функций	72
6.3	Методика построения переходного процесса по обобщенной вещественной частотной характеристике	76
6.4	Ошибки и их составляющие в САУ	78
6.5	Ошибки САУ при типовых режимах работы	79
6.6	Метод коэффициентов ошибок	81
6.7	Структурная неустойчивость САУ	83
6.8	Граница устойчивости и область устойчивости в плоскости одного и двух параметров	84
7	Анализ качества САУ	88
7.1	Критерии апериодичности переходного процесса	89
7.2	Оценка качества САУ по расположению корней	90
7.3	Интегральные оценки качества САУ	94
7.4	Оценка качества САУ по частотным характеристикам	97
8	Улучшение качества САУ	100
8.1	Введение производной в закон регулирования	100
8.2	Введение интеграла в закон регулирования	102
8.3	Создание инвариантных САУ	103
8.4	Создание комбинированных САУ	105
8.5	Многомерные автоматические системы	107
9	Нелинейные системы	110
9.1	0сновные типы нелинейностей	111
9.2	Построение переходных процессов в релейных системах	115
9.3	Устойчивость нелинейных систем	120
9.4	Устойчивость релейных систем	123
9.5	Условия устойчивости нелинейной системы в "малом"	127
9.6	Автоколебания в релейных автоматических системах	131
9.7	Вынужденные колебания в релейных системах	135
9.8	Линеаризация релейных систем	138
9.9	Метод гармонической линеаризации	143
9.10	Метод фазового пространства	153
	Литература	165

1 ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

1.1 Введение

Теория автоматического управления (ТАУ) есть наука, разрабатывающая принципы управления системами и необходимые для этого средства, методы анализа и синтез этих систем.

За последние годы сфера применения теории управления расширилась на столько, что к ней стали относить статистическую динамику, процессы управления движением летательных аппаратов, проблемы игровых ситуаций, вопросы адаптации, теорию оптимального управления, аналитическое конструирование приборов и регуляторов. Управление стало проникать в сферу социальной деятельности человека.

Принципиально новый оттенок теории автоматического управления придали вычислительные машины. Развившись самостоятельно, они стали постепенно входить составной частью в сложные автоматические системы.

Теория управления в настоящее время стала составной частью и техническим фундаментом науки ХХI века - технической кибернетики, главную сущность которой составляет всеобъемлющая теория управления живой и неживой природой.

Академик А.И. Берг, возглавивший кибернетическое направление в СССР, говорил: «Кибернетика стала наукой об общих принципах управления и о применении их в технике, человеческом обществе и в живых организмах».

Кроме умения ставить задачу по жизненным явлениям, т.е. уметь формализовать жизненную ситуацию в данной области науки и техники, инженер должен уметь решать неспецифические задачи (задачи, связанные с добыванием информации, ее хранением, умением сотрудничать с людьми, распределять функции между ними, управлять человеческими коллективами, производственными процессами).

Хотя принципы управления человеческими коллективами и производственными процессами имеют свои специфические особенности, однако они имеют и много общего. Поэтому, изучая курс «Теории автоматического управления», специалист получает интересную информацию, которую можно использовать в самых разнообразных сферах человеческой деятельности. Широкое внедрение в производ­ство автоматизированных систем управления требует от инже­нера более высокой обшей культуры и особенно по вопросам управления.

Управление с применением ЭВМ можно рассматривать как со­во­купность организационных, методических и технико-экономических решений для осуществления воздействий на управляе­мый объект с целью поддержания или улучшения его функцио­нирования.

Для осуществления управления необходимо иметь:

а) цель управления;

б) ресурсы для обеспечения работы управляемых объектов;

в) органы управления, обладающие правом изменять или перераспределять ресурсы с целью достижения цели управле­ния.

Природа системы может быть различна, но во всех слу­чаях в ней можно выделить управляющую часть, управляемый комплекс процессов или объектов, контрольно-измерительные и задающие устройства.

Функционирование реальных систем ограничивается обла­стью их допустимых состояний, как в части многомерных переменных, так и их количественных значений процесс управ­ления заключает­ся в том, чтобы из множества состояний, которые может принимать система, выбрать наиболее рациональные с точки зрения поставленной цели. В частном случае задача сводится к стабилизации управляемого объекта, когда необходимо скомпенсировать все внешние и внутренние возмущения.

В условиях современной экономики теория автоматического управления является одним из главных направлений технического про­цесса, она является основой правильного выбора решения (управления), организации труда.

1.2 Краткая историческая справка раз­вития теории автоматического управления

К первым промышленным регуляторам относятся регуля­торы уровня паровой машины Н.Н.Ползунова (1765 г.).

Начало теории управления было положено работами Максвелла в 1868г. «О регуляторах», и в 1876 г. И.А. Вышнеградского «О регуляторах прямо­го действия». До этих работ исследователи изучали регулятор отдель­но от ма­шины.

Максвелл и Вышнеградский впервые исследовали регулятор и машину как единую динамическую систему, упростили за­дачу, линеаризовав ее, что позволило дать общие методы ис­следования динамики систем регу­лирования.

Ответом на запросы теории были критерии устойчивости Рауса (1874 г.) и Гурвица (1895 г.), откликнувшихся на просьбу Максвелла и Стодолы, который ввел безразмерную форму записи уравнений динамики. Н.Е.Жуковским был написан первый русский учебник «Теория регулирования хода машин». Основы общей теории устойчиво­сти были заложены А.М. Ляпуновым в работе «Общая задача об устойчивости движения», 1829 г.

Н.Н.Вознесенский является создателем одной из круп­ных школ в области теории автоматического управления (ТАУ), основоположником теории автономных систем.

В 1932 г. американский ученый Найквист предложил кри­терий устойчивости, основанный на частотных характеристи­ках, для анализа работы радиотехнических усилителей. В 1938 г. А.В. Михайлов обоб­щил этот критерий для систем ав­томатического регулирования.

Крупный вклад в развитие ТАУ внесли и вносят выдаю­щиеся советские ученые А.А.Андронов, Л.С.Понтрягин, А.Г. Ивахненко, А.А.Фельдбаум, В.В.Солодовников, Е.П.Попов, Л.С. Гольдфорб, Я.З.Цыпкин, М.А.Айзерман, В.А.Трапезников, А.А. Воронов и другие.

3. Основные элементы САУ

Системой автоматического управления (САУ) называется динами­ческая система, обладающая свойствами сохранять требуемую функциональную связь между некоторыми, описывающими ее по­ведение величинами пу­тем сравнения функций этих величин и использования полученных разностей для управления источ­никами энергии.

В качестве величин, характеризующих состояние САУ, могут слу­жить заданное и действительное значение регулируе­мой величины.

Регулируемой величиной называется физическая вели­чина, кото­рой необходимо управлять.

Управляющей называется физическая величина, в соот­ветствии с которой необходимо управлять регулируемой вели­чиной.

Исходя из определения САУ, она может быть в общем виде предс­тавлена, как это показано на рисунке 1.1

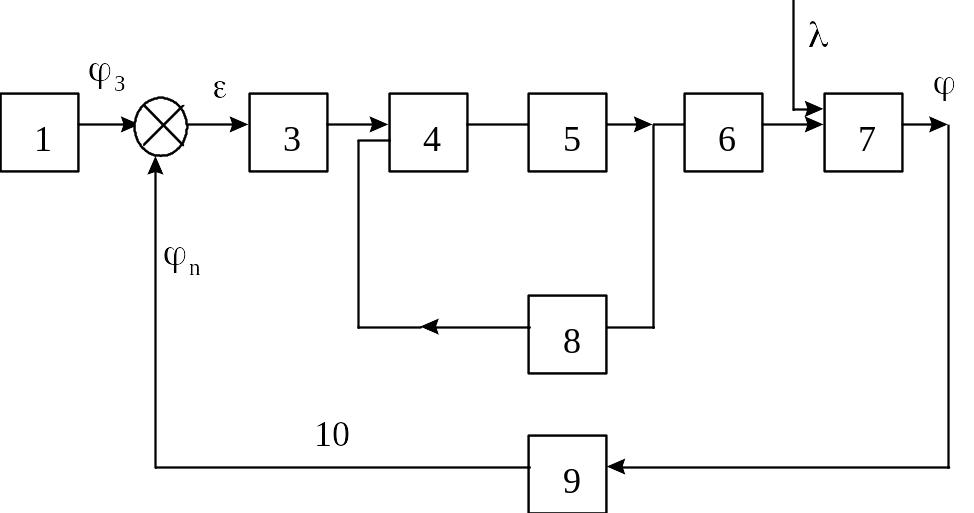
Рисунок 1.1 - Элементная схема САУ

1 - задающий элемент; 2 - эле­мент сравнения заданного и измеренного значения регулируемой величины, выделяющий сигнал ошибки (рассогласования) ; 3 - корректирующий элемент (регулятор), служащий для получения управляющего воздействия в соответствии с желаемым законом управления; 4 - усилительный элемент, усиливающий управляющий сигнал, полученный в регуляторе; 5 - исполнительный элемент (механизм); 6 - регулирующий орган; 7 - объект регулирования; 8 - местная обратная связь; 9 - измерительный элемент; 10 - главная обратная связь; -возмущающее воздействие; -регулируемая ве­личина.

Всякое воздействие, которое стремится нарушить требуемую функциональную связь между управляющей и регулируемой ве­личиной называется возмущающим.

Разность между заданным и измеренным зна­чением регулируемой величины в установившемся режиме назы­вается статической ошибкой (отклонением) регулирования .

В каждом конкретном случае САУ может иметь дополнитель­ные элементы или не иметь некоторых из указанных выше, например, элемента внут­ренней или главной обратной связи, усилителя.

3. Классификация систем управления

Существует множество признаков, по которым можно проводить классификацию САУ.

Наиболее удобным классификационным признаком для САУ является используемая информация об управляемом процессе или системе, рисунок 1.2.

Информацией называется совокупность сведений, первоисточником которых является опыт, служащих для описания состояния физической системы.

Единицей количества информации является бит, харак­теризующий степень неопределенности системы, имеющей два равновероятных состояния. Степень неопределенности сис­темы характеризуется энтропией , которая численно равна математическому ожиданию логарифма со зна­ком минус вероятности любого состояния системы

(1.1)

где - вероят­ность -го состояния системы.

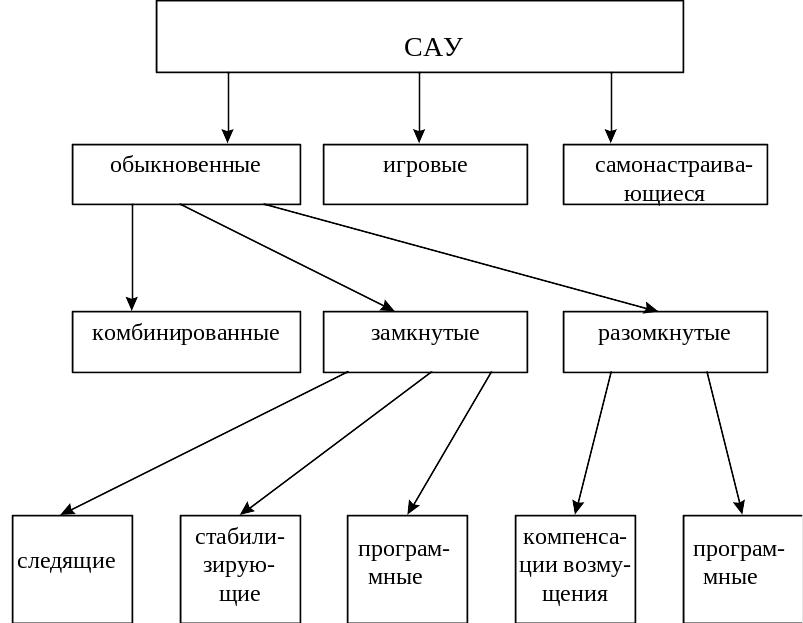
Рисунок 1.2 - Структура классификации САУ

При вычислении энтропии можно выбрать любое основание для логарифмирования, но чаще всего используют двоичные единицы энтропии или бит. Для системы с двумя равновероят­ными состояниями

дв. ед. (бит).

Количество информации, полностью определяющее состояние систе­мы, численно равно энтропии, которой обладала система до получе­ния информации. В общем случае количество инфор­мации определяется величиной уменьшения энтропии системы

, (1.2)

где индексы и относятся к моментам времени до и после получения получе­ния информации.

При измерении объемов информации часто применяется бай­товая система. Байт состоит из 8 битов. В этом случае в каждом байте запоминаются две десятичные цифры или бук­венный знак.

При классификации САУ по информационному признаку сле­дует раз­личать два вида информации: начальную или априор­ную и рабочую ин­формацию.

Априорной называется информация об управляемом про­цессе, необходимая для построения и функционирования САУ, имеющаяся до нача­ла функционирования САУ.

В системах, которых изменение свойств процессов не оп­ределяется, необходимо большое количество априорной ин­формации в целях управления. Такая информация называется полной начальной информацией и характеризует не ее объем, а относительное ее ко­личество, потребное для управления системами других классов.

Необходимость полной информации присуща обыкновенным система не обладающим способностью приспособления к из­меняющимся услови­ям и свойствам управляемого процесса.

Самонастраивающиеся системы - это системы, которые требуют меньше априорной информации для обеспечения требуемой точ­ности и обладают способностью в той или иной мере приспо­сабливаться к изменяющимся внешним условиям. К ним отно­сятся системы экстремального регулирования, системы с самонастраивающимися устройствами, самооптимизирующиеся системы.

Игровые системы - это такие системы, формирование ко­манд кото­рых осуществляется на основе сопоставления множе­ства решений и вы­бора на каждом этапе управляющей операции. Критерием сопоставле­ния решений является показатель, име­нуемый функцией выгод.

Наиболее распространенными являются обыкновенные САУ, которые могут быть замкнутыми и разомкнутыми. Разомкнутые системы в свою очередь делятся по виду рабочей информации на системы компенса­ции и системы программного управления.

В замкнутых системах рабочей информацией является от­клонение координат регулируемого процесса от заданных значений.

Замкнутые системы по виду рабочей информации, опреде­ляющей характер воздействий, разделяются на стабилизирую­щие, следящие и программные САУ.

Существует большое многообразие других признаков для класси­фикации САУ: прямого и непрямого действия, линейные и нелинейные, импульсные, дискретные и непрерывные, элек­трические, пневматиче­ские, гидравлические и др.

1.5 Замкнутые и разомкнутые САУ

В разомкнутых системах автоматического управления (рисунок 1.3 а,б) регулирующее устройство РУ вырабатывает управляющее воздействие без учета значения регулируемой величины . Так, например, на рисунке 1.3(а) представлена сис­тема, позволяющая открывать регули­рующий орган и, если заранее известна функциональная связь , управлять регулируемой величиной . Однако, если функ­циональная связь нарушается из-за наличия возму­щений, то возникает необходимость их учета. С этой целью измеряется наиболее существенное возмущение (или не­сколько возмущений) и через корректирующее устройство КУ сигнал, пропорциональный воз­мущению, вводится в РУ, рисунок 1.3(б). КУ вырабатывает управляющее воздействие с учетом возмущения, что позволяет компенсировать влияние на .

Принцип управления по возмущению обладает высоким бы­стродей­ствием, поскольку управляющее воздействие появля­ется одновремен­но с возмущающим, однако не может быть ре­ализован при большом ко­личестве возмущений из-за сложности системы и большого количест­ва измерительных и корректирую­щих устройств.

Индикатором наличия возмущения по любому каналу САУ яв­ляете отклонение измеренного значения регулируемой величины от заданного. Оно является интегральной оценкой влияния всей совокупности возмущений на САУ. Это обстоятельство по­зволяет создавать САУ, работающие по отклонению регулируе­мой величины (рисунок 1.3в). Однако у таких систем имеется не­достаток, заключающийся в появлении управляющего воздейст­вия только после наличия отклонения, т.е. система обладает низким быстродействием. Для устранения указанного недостатка используются комбинированные системы (рисунок 1.3г), позволяющие объединить достоинства систем, работающих по возмущению и отклоне­нию. Кроме того, система, работающая по отклонению, является замк­нутой системой. Управляющее воздействие выра­батывается с учетом текущего значения регулируемой вели­чины. Это достигается благода­ря наличию главной обратной связи и элемента сравнения, позволяю­щего сравнить заданное и действительное значение регулируемой ве­личины и исполь­зовать результаты сравнения для создания управляющего воз­действия

. (1.3)

а) в)

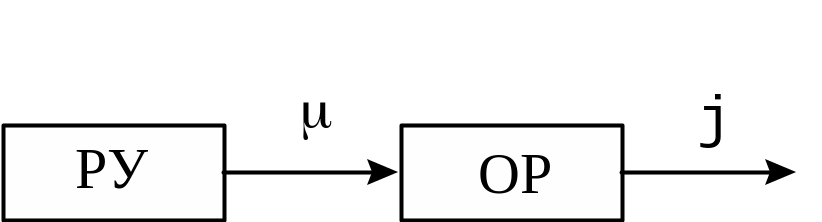
б) г)

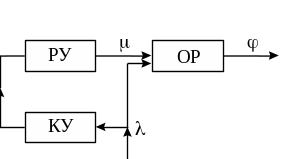
Рисунок 1.3 – Принципы управления в САУ

Статика - установившийся режим работы САУ, когда все величины, характеризующие ее состояние, не зависят от вре­мени, а уравнения и характеристики системы не содержат время.

Динамика характеризует переходный процесс в САУ, изучает не­стационарные режимы. Основной режим работы САУ - динами­ческий. Он описывается дифференциальными уравнениями, соде­ржащими в ка­честве независимой переменной время.

Одной из основных задач динамики является анализ работы систе­мы регулирования, т.е. составление уравнений динамики, совместное их решение и исследование процесса регулирования по найденным результатам.

Более распространенной является задача синтеза, когда необхо­димо найти структуру и параметры звеньев, обеспечи­вающие задан­ное качество процесса регулирования. В задачу синтеза САУ входят вопросы определения настроечных параметров элементов, обеспечивающих требуемое качество переходного процесса при заданной структуре САУ. При этом может иметь место статическая или динамическая нелиней­ность, которая сущест­венно усложняет задачу исследования. Мы ограничимся рассмотрени­ем линейных САУ, для каждого из элементов которой должно быть известно линейное дифференциальное или алгебраическое уравнение, описывающее его статические и динамические свойства.

Статическая характеристика звена или системы характери­зуется коэффициентом усиления, определяемым как отношение приращения выходной величины к приращению входной в уста­новившемся режиме. Для объекта регулирования это

. (1.4)

Динамическая характеристика звена или системы определя­ется ее переходной функцией, которую получают решением дифференциального уравнения при единичном ступенчатом входном воздействии.

2. МЕТОДИКА СОСТАВЛЕНИЯ УРАВНЕНИЙ ДИНА­МИКИ

ОБЪЕКТОВ УПРАВЛЕНИЯ

2.1 Уравнение динамики одноёмкостного объекта

Качество работы систем автоматического регулирования зависит от правильной настройки. Как правило, свойства объ­ектов регулирова­ния зависят от их конструктивных особенно­стей и технологических режимов, а хорошее качество ра­боты всей САУ получают при измене­нии параметров настройки регулятора. Для правильного выбора настро­ек регулятора не­обходимо знать статические и динамические свойст­ва объектов регулирования.

И.А. Вышнеградский впервые показал, что изучать только свойст­ва регуляторов недостаточно, для правильной оценки регулятора необходимо рассматривать действие объекта регу­лирования и регулятора в нестационарных режимах. Математи­чески эта задача сводится к сос­тавлению уравнений динамики объекта и регулятора и совместному их решению.

Процессы, протекающие в объектах регулирования, как правило, описываются дифференциальными уравнениями, которые можно получить различными способами: аналитически, экспери­ментально или экспериментально - аналитически, когда коэффициенты дифференциального урав­нения, полученного ана­литически, определяются экспериментально.

Сложность составления дифференциальных уравнений со­стоит в том, что нельзя совершенно точно описать реальные процессы, необходимо прибегать к идеализации, учитывать ос­новные свойства и пренебрегать второстепенными. В зависимо­сти от степени точности и постановки задачи могут быть и различные идеализации. Например, шар подвешен на пружине и совершает колебания. Если мы рассматриваем колебания в течение малого промежутка времени (1-2 колеба­ния), то шар можно представить как материальную точку массы и пренебречь силами трения. Если мы рассматриваем этот процесс в течение дли­тельного промежутка времени, то нужно учитывать силы трения, ибо в конце процесса рассмотрения эти силы внесут существенные изме­нения в процесс.

Таким об­разом, одна и та же идеализация может быть целесообразной и нецелесообразной в зависимости от того, на какие во­просы мы хотим получить ответ.

Составим дифференциальное уравнение, описывающее про­цесс изме­нения уровня жидкости в баке.

На рисунке 2.1 приняты следующие обозначения:

- объемный приток и расход жидкости; - на­поры жидкости в питающем трубопроводе и у потребителя; , - перемеще­ние штоков регулирующих органов; - уро­вень жидкости в баке; -площадь бака.

Для определенности принимаем за положительные изменения переменных следующие: увеличение уровня, увеличение открытия регули­рующих органов, увеличение расходов через регулирующие органы. Этот выбор является условным, однако должен сохраняться при сос­тавлении всех уравнений.

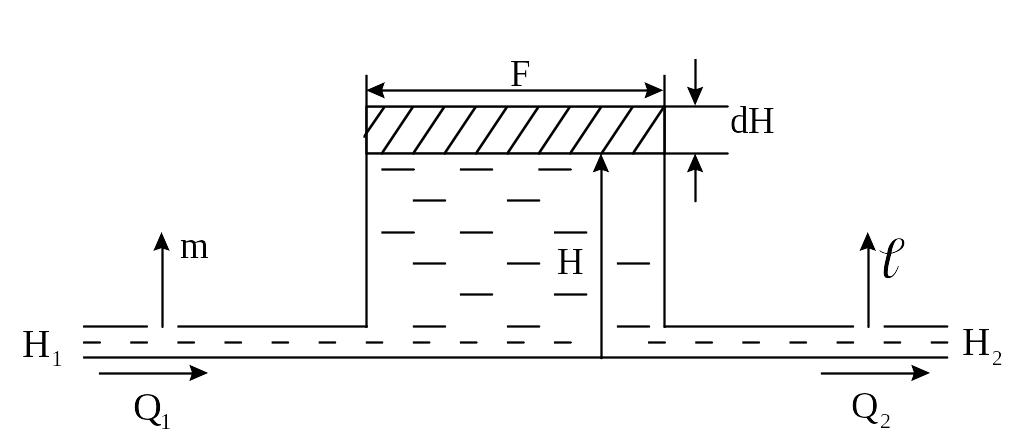
Рисунок 2.1 - Расчетная схема одноёмкостного объекта

Прежде чем приступить к составлению дифференциальных уравнений на основании анализа состояния и условий работы объекта необходи­мо сделать упрощающие допущения. Пусть условия работы объекта позволяют допустить:

1) уровень жидкости в баке не зависит от температуры (жидкость не изменяет своего объема, т.к. температура изменяется незначительно);

2) инерцией потока жидкости пренебрегаем;

3) считаем, что характер движения жидкости через регулирующие органы - ламинарный;

4) давление жидкости в питающем трубопроводе и у потребителя не изменяется.

На основании закона сохранения материи за бесконечно малый промежуток времени при небалансе между и имеем изменение уровня, равное

, (2.1)

или . (2.2)

В установившемся режиме изменение уровня жидкости

отсутствует, т.е. , поэтому

, (2.3)

где и - объемный расход жидкости в установившемся режи­ме.

Если учесть, что и и вычесть из уравнения динамики (2.2) уравнение статики (2.3), то получим уравнение в приращениях: . (2.4)

В левой части уравнения (2.4) имеется производная вместо . Такая замена правомерна, поскольку , т.к. дифференциал от постоянной величины .

В системах регулирования значения и обычно являются неизвестными. Регулятор воздействует на регулирующие органы, положение которых легко определить, поэтому в уравнении динамики (2.4) необходимо заменить расходы и на соответствующие открытия регулирующих органов.

С учетом сделанных допущений расходы через регулирующие орга­ны можно записать следующим образом:

, (2.5)

, (2.6)

где -постоянный коэффициент пропорциональности. Эти зависимости считаем справедливыми как в статике, так и в динамике, поскольку мы сделали допущения, что пренебрегаем инерцией потока. Зависимости (2.5) и (2.6) нелинейные, поскольку имеет место произведение пере­менных.

Для малых отклонений и от установившегося режима зависи­мости (2.5) и (2.6) можно линеаризовать, что значительно упрощает совместное решение системы уравнений. С этой целью функции и разложим в ряд Тейлора в окрестности рабочей точки установившегося режима:

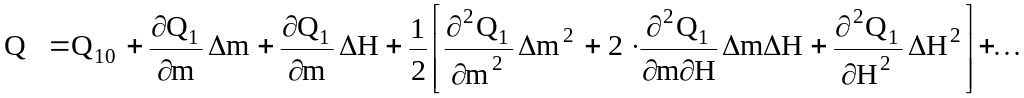(2.7)

Частные производные взяты в рабочей точке , .

Ограничиваясь членами ряда с , и в первой степени, т.е. принимая линейное приближение, получаем:

. (2.8)

Аналогично

. (2.9)

Из выражения (2.7) следует, что указанным методом линеариза­ции можно пользоваться тогда, когда сама функция и ее производные по всем переменным непрерывны, однозначны и конечны.

Из выражений (2.8)и (2.9) находим:

, (2.10)

. (2.11)

Подставим полученные выражения для и в уравнение (2.4):

, (2.12)

или, перенося в левую часть все члены с , находим

. (2.13)

Таким образом мы получили линеаризованное уравнение динамики, ко­торое будет иметь постоянные коэффициенты при переменных лишь при малых отклонениях от исходного статического режима .

В уравнении (2.13) все слагаемые имеют размерность объема. Размерный вид дифференциальных уравнений затрудняет сравнение ди­намики различных по своей природе процессов. Словацкий профессор А.Стодола, разработавший теорию непрямого регулирования, ввел безразмерную форму записи уравнений динамики, повсеместно приня­тую в настоящее время. С этой целью вводятся безразмерные переменные:

; ; ,

где , , - относительное изменение регулируемой величи­ны, регулирующего органа, нагрузки.

Для стационарного режима номинальной и максимальной нагрузки справедливы соотношения:

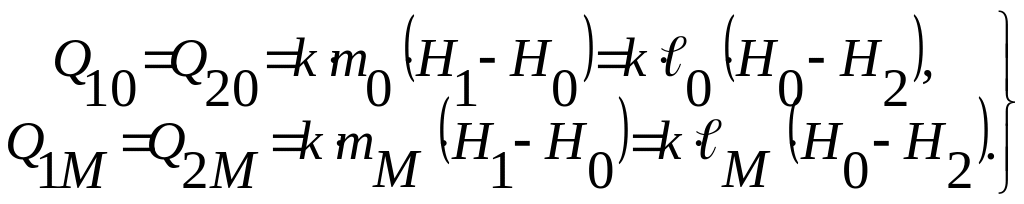(2.14)

Разделим все слагаемые выражения (2.13) на

:

. (2.15)

Если в выражениях (2.14) почленно разделить левые и правые части, то

получим 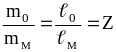, где - коэффициент нагрузки.

Введя безразмерные величины, уравнение (2.15) можно записать в виде:

,

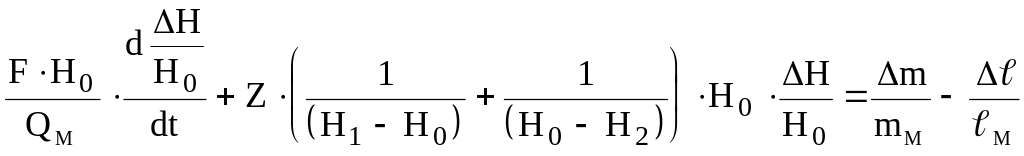или , (2.16)

(2.17)

- коэффициент саморегулирования. Он характеризует способность объекта приходить к новому установившемуся состоянию при нали­чии возмущения. Саморегулирование объекта появляется в результате того, что само изменение регулируемой величины стремится обеспечить баланс притока и расхода жидкости. Пусть . В этом случае растет, создает противодавление на клапане , уменьшает перепад давлений на нем и, соответственно, уменьшает расход . Кроме того, при возрастании Н увеличивается пере­пад давлений на клапане , что приводит к возрастанию , т.е. стремится к . Как видно из зависимости (2.17), коэффициент само­регулирования тем больше, чем меньше перепад давлений на регули­рующих органах и чем больше номинальное значение регулируемой величины.

Если стремится к нулю, а перепад давлений на регулирую­щих органах растет, то коэффициент саморегулирования стремится к нулю. Например, если вместо клапана поставить насос пос­тоянной производительности, а давление ,т.е. расход не зависит от , то . Малейший разбаланс между и приведёт либо к переливу, либо к полному опорожнению емкости.

У некоторых промышленных объектов имеется отрицательное само­регулирование. Например, подача в шаровую мельницу угля больше определенного количества приводит к ухудшению условий работы ша­ров, перемалывание ухудшается и производительность ее падает, что приводит к еще большему накоплению угля внутри мельницы и последующей остановке.

Рассмотрим изменение во времени уровня жидкости в баке для случая положительного и нулевого саморегулирования. С этой целью запишем уравнение (2.16) в виде

(2.18)

где - постоянная времени объекта регулирования,

- коэффициент усиления.

Решим линейное неоднородное дифференциальное уравнение (2.18). Полное его решение состоит из двух слагаемых:

(2.19)

где - свободная составляющая решения, определяемая как об­щее решение линейного однородного дифференциального уравнения; - вынужденная составляющая решения, определяемая частным решением неоднородного дифференциального уравнения.

Характеристическое уравнение имеет вид

(2.2(2.20)

откуда , где - корень характеристического уравнения. В итоге:

В установившемся режиме из уравнения (2.16):

поэтому (2.21)

Постоянную интегрирования находят по начальным услови­ям. Предполагаем, что имеют место нулевые начальные условия, или

поэтому (2.22)

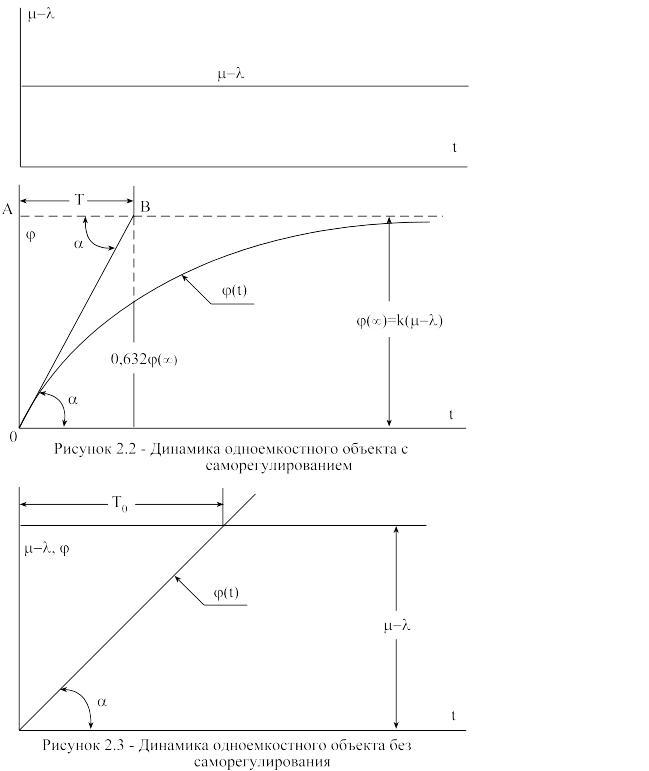
Если на графике построить кривую изменения во времени при скачкообразном возмущении, то она будет иметь вид изображен­ный на рисунке 2.2. Кривая без колебаний приходит к новому установившемуся значению. Динамические звенья с таким видом переходной функции называются апериодическими.

Проведя касательную в точке к кривой до пересечения с установившимся значением , получим отрезок , чис­ленно равный постоянной времени . Действительно, из уравнения (2.22) :

.

Из рисунка и уравнения (2.22) видно, что = =k(m-l),

(2.23)

На основании изложенного следует правило определения постоян­ной времени объекта , имеющей размерность времени.

Постоянная времени апериодического звена T есть время, в течение которого вы­ходная величина объекта достигла бы своего установившегося сос­тояния при скачкообразном изменении входной величины, если бы скорость ее изменения была постоянной и равной в начальный мо­мент времени.

Из уравнения (2.22) также следует, что при :

(2.24)

т.е. постоянная времени есть время, в течение которого выходная величина достигнет от полного изменения ее значения. Исходя из свойства экспоненты, графически легко определить постоянную вре­мени объекта, проведя касательную в любой точке кривой и определив ее проекцию на ось установившихся значений, как отрезок между перпендикуляром, проведенным из точки касания, и точкой пересечения касательной с установившимся значением вы­ходной величины.

Статический коэффициент усиления объекта есть отношение приращения выходной величины к приращению входной в установившемся режиме

(2.25)

Таким образом, если известна зависимость выходной величины объекта во времени при скачкообразном изменении входной, то лег­ко графически определить параметры объекта ( и ) . Этим спосо­бом пользуются при экспериментальном определении параметров объек­та. Для этого скачком наносят возмущение ( ) и непрерывно опреде­ляют значение выходной величины объекта. Кривая , полу­ченная экспериментальным образом при скачкообразном воздействии на входе, называется кривой разгона. Если кривая разгона по форме близка к экспоненте и не имеет точки перегиба, то, пользуясь методикой, рассмотренной ранее, определяют коэффициенты дифференциального уравнения (2.18).

Определим переходную функцию объекта, когда коэффициент са­морегулирования . В этом случае дифференциальное уравнение (2.16) принимает вид:

(2.26)

откуда (2.27)

Переходная функция имеет вид прямой, проходящей через нача­ло координат. График переходной функции изображен на рисунке 2.3.

. (2.28)

В случае нулевого саморегулирования объект регулирования пред­ставляет идеальное интегрирующее звено. Постоянная времени интег­рирующего звена есть время, в течение которого выходная вели­чина достигнет значения входного скачкообразного воздействия (следует помнить, что дифференциальное уравнение записывают в безразмерной форме).

Аккумулирующая способность бака зависит от величины его емкос­ти. Чем больше эта емкость, тем медленнее будет изменяться отно­сительное значение уровня при нарушении небаланса между притоком и потреблением. Под емкостью объекта регулирования понимают его способность накапливать энергию (механическую, электрическую и тепловую) или вещество

(2.29)

где - емкость объекта регулирования.

Отношение емкости объекта к величине измеряемого параметра называется коэффициентом емкости (удельной емкостью):

(2.30)

т.е. в нашем случае коэффициент емкости определяет площадь ре­зервуара.

Рассмотренный выше объект называется одноёмкостным, т.к. для него характерно наличие одной емкости.

Многие промышленные объекты являются более сложными системами, которые могут вклю­чать несколько емкостей и сопротивлений и, следовательно, будут описываться более сложными дифференциальными уравнениями. Такие объекты называются многоёмкостными.

2.2 Уравнение динамики двухъёмкостного объекта

Примером двухъёмкостного объекта может служить гидравлическая система, состоящая из двух баков, накапливающих жидкость, если регулируемой величиной является уровень в одном из баков, а управляющими воздействиями служат приток или отбор жидкости из баков, как это показано на рисунке 2.4.

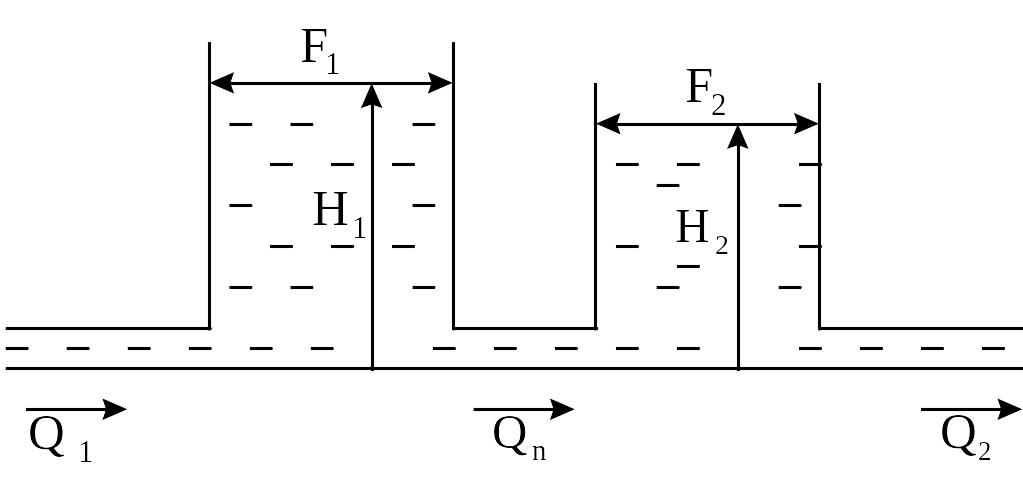
Рисунок 2.4 Расчетная схема двухъёмкостного объекта

В электрических системах в качестве накопителей могут служить ёмкости или индуктивности, в тепловых системах тепловая энергия накапливается в элементах, обладающих значительной теплоемкостью, например, в змеевиках нагре­вателей, в массе вещества, стенках аппаратов и т.д. Для каждой отдельной ёмкости, независимо от физической природы процессов, может быть записано дифференциальное уравнение, имеющее одну и ту же форму:

(2.31)

где - удельная ёмкость (тепловая, электрическая, геометрическая); - выходная величина звена (температура, напряжение, уровень); , - поток, увеличивающий и уменьшающий выходную величину (тепловой поток, ток, объемный расход).

Сделав допущения, аналогичные допущениям для одноемкостного объекта (пренебрегаем инерцией потока, уровень в емкостях не за­висит от температуры, давление в питающем трубопроводе и у потре­бителя остается постоянным и не влияет на расход). Предположим, что мы можем управлять непосредственно потоками и , например, с помощью насосов регулируемой производительности, а переток линейно зависит от разности уровней.

В соответствии с общей методикой составления уравнений дина­мики запишем уравнения нестационарного режима:

(2.32)

Уравнения статического режима:

(2.33)

Если учесть, что текущее значение переменной может быть записано как сумма установившегося значения и отклонения, то

(2.34)

Вычитая из уравнения динамики уравнение статики, а также учитывая соотношение (2.34), получаем:

	(2.35)
	( (2.36)
	(2.37)

Из уравнений (2.35) и (2.37)

(2.38)

Из уравнений (2.36) и (2.37)

(2.39)

Дифференцируя уравнение (2.39), получаем

( (2.40)

Подставив значения из уравнения (2.39) и из уравнения (2.40) в выражение (2.38), получим:

(2.41)

Для перехода к безразмерной форме записи уравнения (2.41) сделаем обозначения:

Разделив все слагаемые (2.41) на и учитывая обозначения, получим:

		(2.42)
Обозначив

Окончательно получим: (2.43)

Сделав аналогичные преобразования, можно получить дифференциальное уравнение относительно j₁, которое имеет вид

.

(2.44)

2.3 Уравнение динамики объекта с двумя регулируемыми величинами

Рассмотренный ранее двухъёмкостный объект может служить приме­ром объекта с двумя регулируемыми величинами, если таковыми будут являться уровень в первом и втором баках, а объектом регулирова­ния считать систему из двух баков.

Часто приходится встречаться с объектами, в которых необходи­мо поддерживать различные регулируемые величины (давление, уровень концентрации, уровень; температуру, концентрацию и т.д.), изменение одной из которых приводит к изменению другой. Такие объекты назы­ваются объектами с несколькими взаимосвязанными величинами. Рас­смотрим в качестве примера аппарат, в котором необходимо поддержи­вать постоянными уровень и концентрацию вещества (рисунок 2.5).

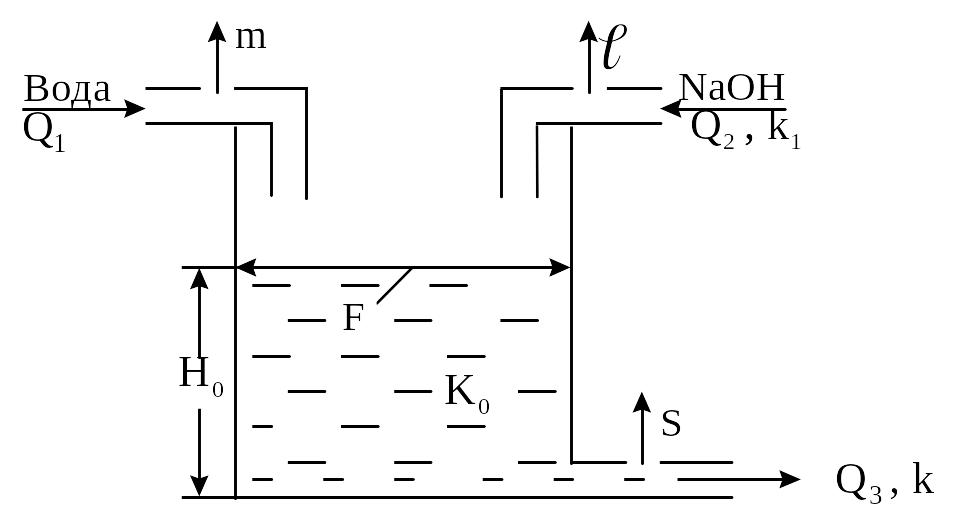
Рисунок 2.5 - Расчетная схема объекта с двумя регулируемыми величинами

Сделаем следующие упрощающие допущения:

1. Пренебрегаем инерцией потока жидкости.

2. Температура жидкости постоянна.

3. Давление жидкости в подводящих трубопроводах постоянно.

4. Характер движения жидкости ламинарный.

5. Концентрация постоянна.

6. Расход пропорционален открытию регулирующих органов.

Составим уравнение динамики для изменения уровня в баке:

(2.45)

Аналогично можно написать уравнение баланса для щёлочи:

(2.46)

Для условия статики получим:

	(2.47)
	(2.48)

Вычитая из уравнения динамики (2.45) и баланса (2.46) уравнения (2.47) и (2.48), соответственно, получаем уравнения в приращениях:

(2.49)

(2.50)

Уравнение (2.50) нелинейно, т.к. в слагаемых есть произведение переменных.

Линеаризуем его.

(2.51)

Подставим в уравнение (2.51) выражение (2.49):

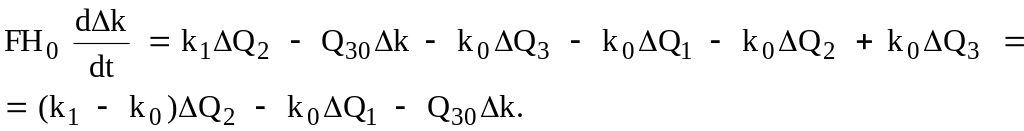(2.52)

Обозначим:
— коэффициент нагрузки.		(2.53)

Используя указанные обозначения, из соотношений (2.49) и (2.52) получаем:

		(2.54)
		(2.55)
или		(2.56)

Здесь Выражения (2.55) обычно записывают в виде:

(2.57)

Выясним, можно ли управлять объектом с двумя регулируемыми величинами одним регулирующим органом. Из уравнения (2.55) видно, что в статике должна быть жесткая связь между m₁ и m₂. Действительно, из второго уравнения системы (2.56) следует, что при j₂’=j₂=0:

.

Поскольку , то для удовлетворения условия j₁’=0 из первого уравнения системы (2.56) следует, что

.

Это условие указывает на то, что не должно иметь жесткой связи с и , кроме того, должно изменяться при изменении l; одновременно не могут выполняться оба условия для . Таким образом, для управления объектами с несколькими регулируемыми величинам необходимо иметь количество регулирующих органов, причем их количество должно быть не меньше количества регулируемых величин.

3 АНАЛИЗ САУ В ПРОСТРАНСТВЕ СОСТОЯНИЙ

3.1 Вектор состояния непрерывной САУ

Развитие вычислительной техники, теории информации, теории управления привело к пробуждения интереса к классическим методам фазового пространства для анализа систем, описываемых векторными дифференциальными уравнениями (разностными) первого порядка. Метод пространства состояний начал играть главную роль в теории оптимальных систем, как имеющих ограничения, так и без них.

Наиболее простой и наглядный метод установления соответствия вектора состояния заданной непрерывной системы есть метод реализаций.

Существо метода заключается в том, что находится некоторая эквивалентная исходной система, реализуемая в виде соединения сумматоров, усилителей, интеграторов, дифференциаторов.

Для того, чтобы установить соответствие вектора состояния реализованной системе, назначают компонентами выходы всех интеграторов и входы всех дифференциаторов, исключая дифференциаторы, соединяемые с выходом какого-то интегратора через усилители.

Пусть система описывается уравнением вход - выход вида

1. 

Передаточная функция такой системы

(3.1)

Для такой системы легко реализовать систему , состоящую из интеграторов. Из выражения для передаточной функции следует:

Используя интеграторов и один операционный усилитель, схему реализации представим в таком виде, где

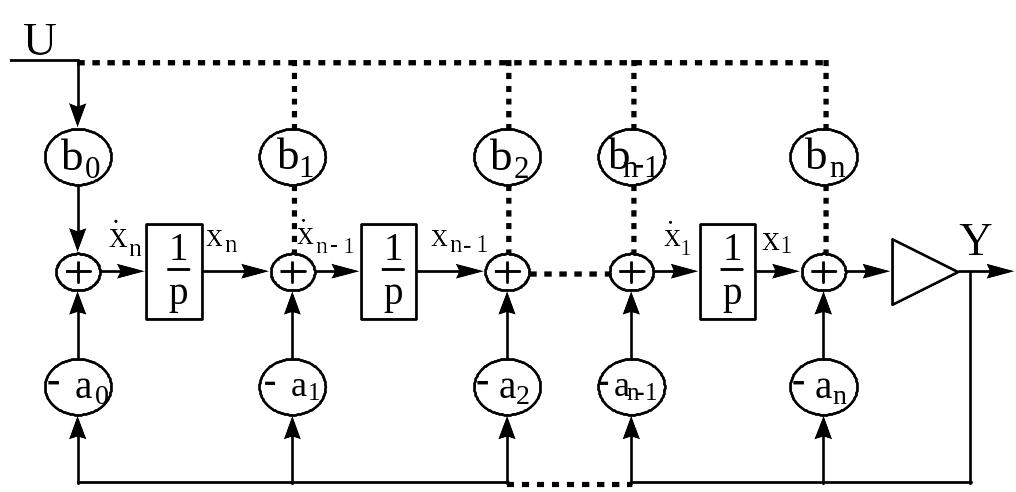
Рисунок 3.1 - Схема реализации эквивалентной системы.

Соотношения, определяющие , будут:

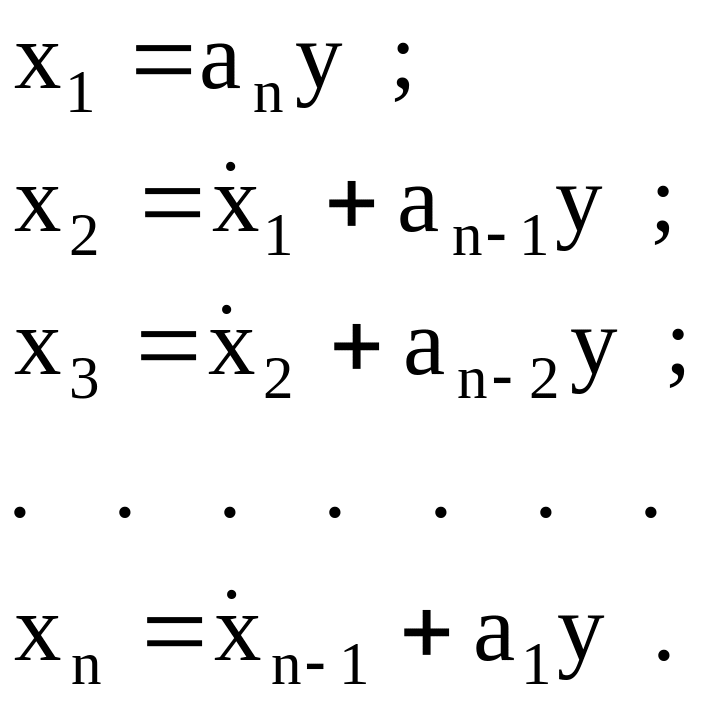(3.2)

Для вектора соотношения получаются из , если учесть, что (коэффициент ).

Используя это соотношение, можно записать зависимости:

(3.3)

Эту же систему можно реализовать другой схемой, изображенной на рисунке 3.2

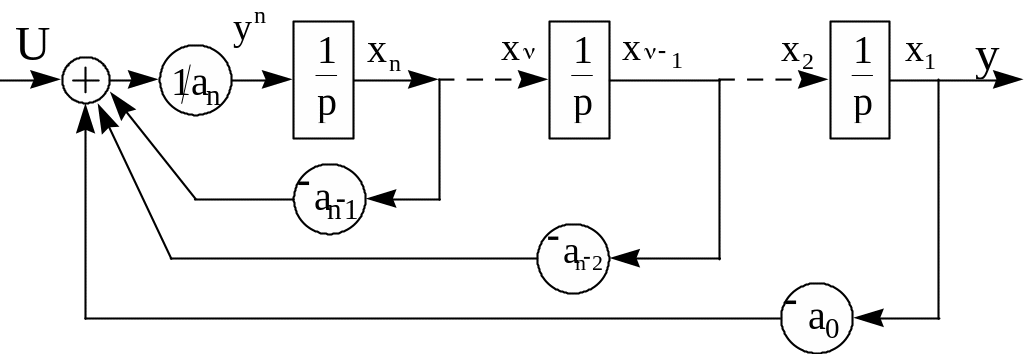
Рисунок 3.2 - Схема реализации эквивалентной системы без производных в правой части

Очевидно, что

Для данной схемы справедливы следующие соотношения:

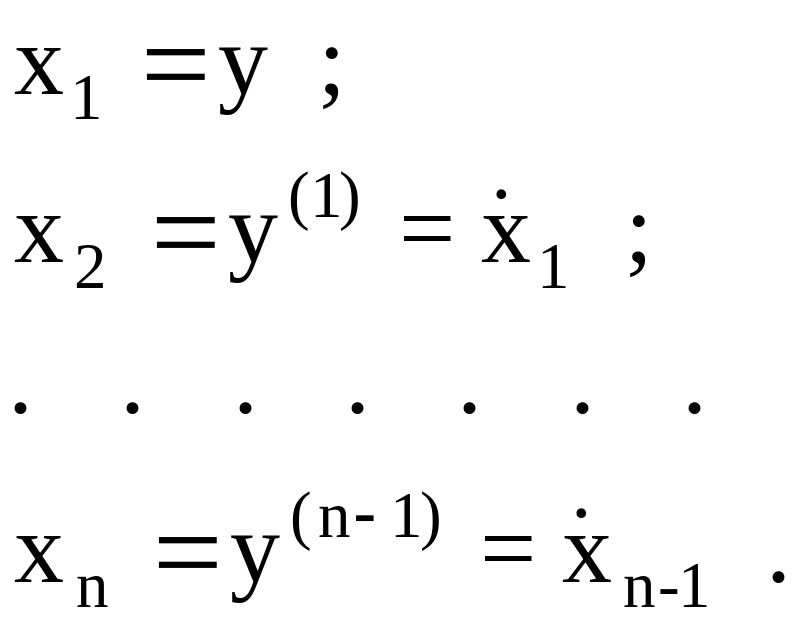(3.4)

Для вектора составляющие принимают значения:

(3.5)

Таким образом, пространство состояний исходной системы зависит от схемы ее реализации.

Для общего случая, когда исходная система описывается уравнением входа-выхода вида

(3.6)

схема реализации изображена на рисунке 2.1 с учетом пунктирных линий.

Выбирая компоненты вектора в соответствии с принятым правилом, получаем следующие соотношения:

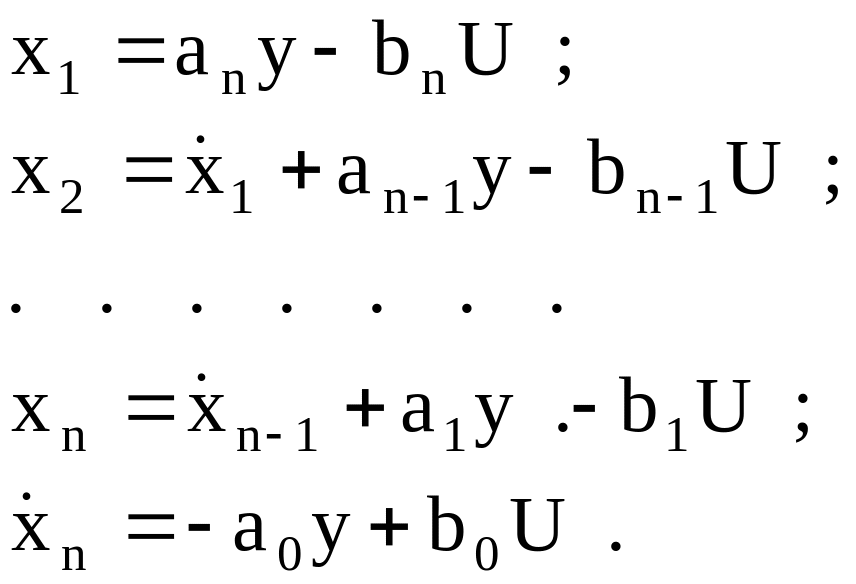(3.7)

Решая эти уравнения относительно и и выражая их через и , получаем:

(3.8)

Полученную систему уравнений можно записать в канонической форме

(3.9)

где

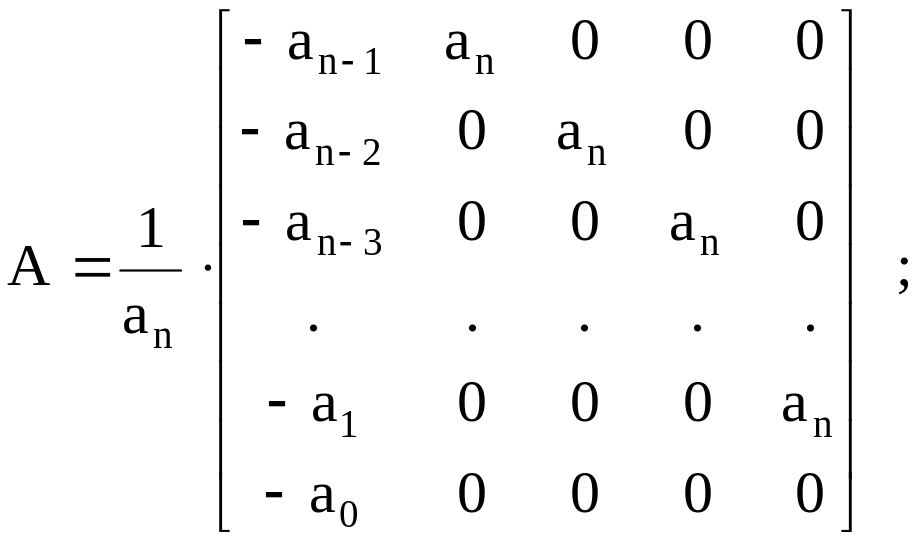
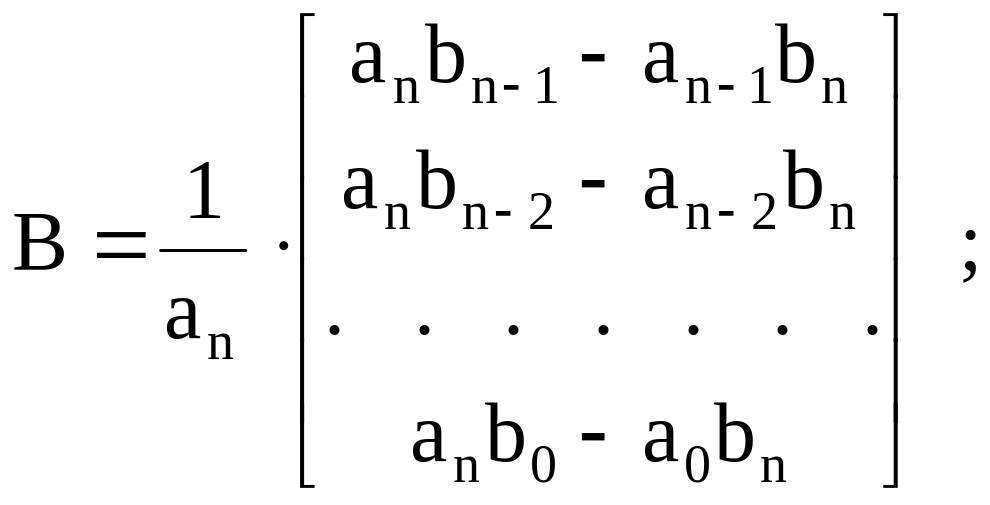
Известны и другие методы, позволяющие избавиться от производных в правых частях уравнений, когда коэффициенты не равны нулю.

На практике часто процесс описывается системой дифференциальных уравнений с переменными коэффициентами. Кроме того, система подвержена влиянию случайных помех, приложенных к различным ее точкам. В этом случае система описывается системой обыкновенных дифференциальных уравнений:

(3.10)

, или в векторно-матричной форме

где , , - параметры физической системы.

3.2 Переходная матрица состояния

В практических расчетах необходимо иметь решение уравнения (3.3) в явном виде. Его можно получить с помощью переходной матрицы состояния.

Система уравнений (3.3) линейная и неоднородная, следовательно, ее решение состоит из общего решения однородной и частного решения неоднородной системы уравнений.

Общее решение однородной системы уравнений

(3.11)

будем искать в виде

(3.12)

где - неизвестная матрица размерности . Подставив (3.12) в (3.11), получаем выражение

или

(3.13)

Оно должно выполняться для всех .

Поскольку - произвольный вектор, то это равенство выполняется тогда и только тогда, когда удовлетворяет матричному дифференциальному уравнению

(3.14)

для всех .

При из (3.12) находим

(3.15)

Начальные условия для (3.14) получаются из (3.15):

где - единичная матрица размером .

Отсюда видно, что

(3.16)

Таким образом, общее решение уравнения (3.11) можно записать в виде (3.12), где удовлетворяет начальным условиям (3.16), т.е.

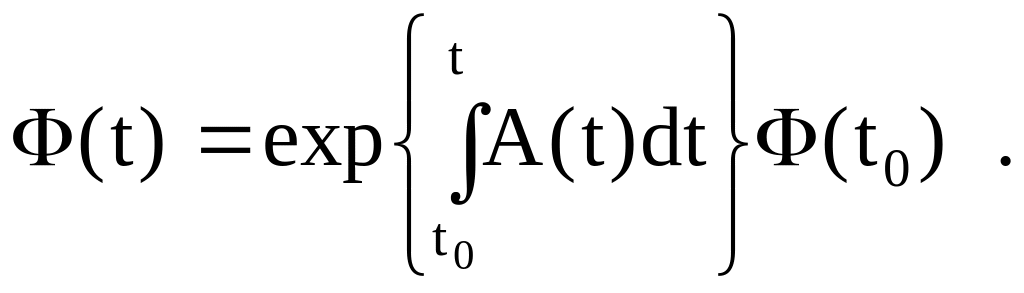
Частное решение уравнения (3.3) можно получить методом вариации постоянных. Положим, что решение имеет вид

(3.17)

где - определяется как и раньше, а - неизвестный - вектор.

Подставив выражение (3.17) в уравнение (3.3), получим:

(3.18)

Поскольку , то это выражение можно записать так:

или

(3.19)

Предполагается, что в уравнении (3.19) матрица не особая. Интегрируя уравнение (3.13), получаем:

(3.20)

которое с учетом выражения (3.17) принимает вид:

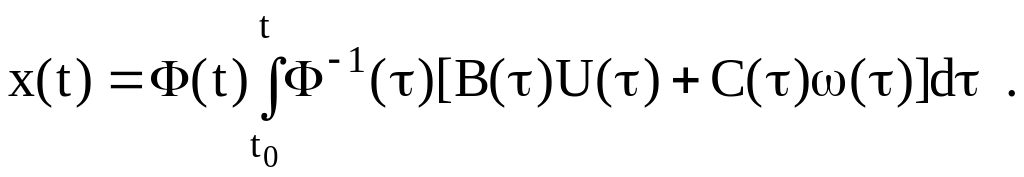(3.21)

Объединив частные решения (3.21) с общим решением (3.12), получаем полное решение исходного математического уравнения (3.3):

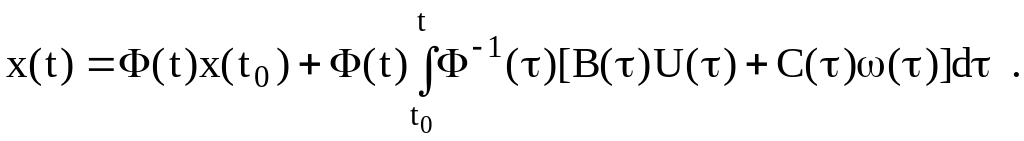(3.22)

Матрица называется фундаментальной матрицей системы (3.3). Следует обратить внимание на то, что она полностью определяется матрицей динамической системы .

Обозначим

(3.23)

Матрицу называют переходной матрицей состояния системы. Она обладает следующими свойствами:

1. так как .

2. Поскольку то

Для получения необходимо решить дифференциальное уравнение

при начальном условии и заменить на .

3.

Это свойство вытекает из уравнения (3.23) при ,

4.

для всех . Используя (3.23) можно записать:

5. для всех .

Действительно,

В итоге решение уравнения (3.3), записанное в виде (3.22), можно представить так:

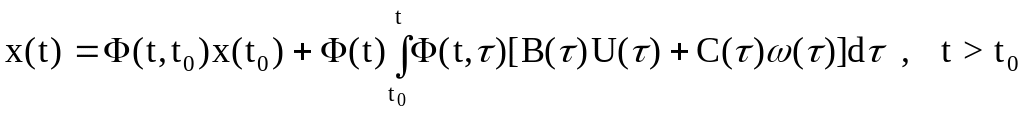. (3.24)

Если матрица , , постоянна, то систему называют системой с постоянными коэффициентами, или стационарной системой. В этом случае фундаментальная матрица системы

(3.25)

Переходная матрица состояния системы с постоянными коэффициентами:

(3.26)

Существуют и другие методы вычисления , например, с помощью преобразования Лапласа, матрицы собственных векторов или путем интегрирования одного дифференциального уравнения (3.11) с последующим определением постоянных интегрирования из начальных условий.

4 ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ПРОСТЕЙШИХ ЗВЕНЬЕВ

4.1 Типовые входные сигналы

Исследование свойств звеньев или систем управления может быть проведено по реакции на одинаковые входные сигналы. В качестве ти­повых входных сигналов используются различные функции.

а) ступенчатая функция, аналитическое выражение которой можно записать так:

Функция называется единичной ступенчатой функцией. Реакция звена или системы управления на единичную ступенчатую функцию называется переходной функцией. Она может быть получена путем решения дифференциального уравнения при единичном ступенчатом входном воздействии. Если реакция звена или системы на ступенча­тое входное воздействие получена экспериментально, то она называется кривой разгона. Поскольку , а ,

то - переходная функция звена или

системы, имеющей передаточную функцию .

б) импульсная функция. Является производной ступенчатой функции и обозначается . Она представляет импульс бесконечно большой величины и бесконечно малой длительности интеграл от которой . Реально такой импульс иметь нельзя, одна­ко являясь математической идеализацией, он облегчает исследование САУ. Изображение можно получить с помощью предельного перехода для изображения импульсного сигнала, когда его амплитуда стремится к бесконечности, а длительность к нулю.

.

Переходная и импульсная переходная функция называются временными характеристиками звена или системы.

.

в) гармоническая функция. Она может быть задана в веществен­ной или комплексной форме:

, или ,

где -угловая частота; - период колебаний.

Весьма удобной при исследовании CАУ оказывается комплексная форма задания гармонической функции:

.

При этом интерес представляет способность звена или системы воспроизводить входной сигнал на выходе, т.е. частное реше­ние неоднородного дифференциального уравнения которое также представляет гармоническую функцию, но с амплитудой и фазой, отличной от входного воздействия. Амплитуда и фаза выходной величины зависят от частоты и параметров системы. Поэтому исследование реакции звена или системы на гармоническое воздействие приводит к понятию частотных характеристик.

Пусть на САУ действует гармоническое воздействие. Тогда частное решение дифференциального уравнения будет также гармонической функцией, но отличающейся от входного воздействия по амплитуде и фазе.

; ,

,

и т.д.

Если имеется дифференциальное уравнение

, (4.1)

то, заменив в нем значения входного и выходного сигналов и производных, получим

.

Отношение установившегося гармонического сигнала на выходе звена или системы к гармоническому входному сигналу называется амплитудно-фазовой характеристикой (АФХ)

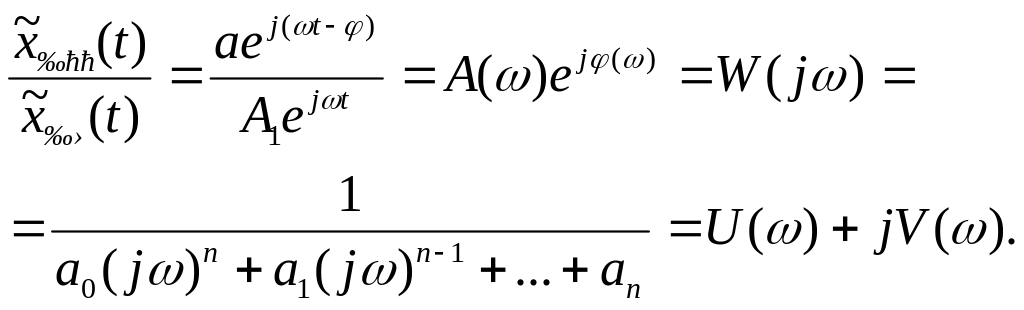(4.2)

где - вещественная часть амплитудно-фазовой характеристики; - мнимая часть амплитудно-фазовой характеристики.

В выражении (4.2) есть амплитудно-частотная характеристика; - фазочастотная характеристика.

Формально амплитудно-фазовая характеристика может быть получена путем замены в передаточной функции на . Действительно, дифференциальное уравнение (4.1) в операторной форме имеет вид:

,

откуда передаточная функция

,

амплитудно-фазовая характеристика

.

Весьма удобными при синтезе САУ являются логарифмические частотные характеристики, позволяющие производить выбор пара­метров звеньев при заданной структуре САУ, удовлетворяющих требуемому качеству, выбор структуры и параметров корректирующих звеньев.

При этом используется акустическая система единиц. Считают, что две частоты отличаются на октаву, если , и на декаду, если . Мощности сигналов отличаются на Бел, если , и на децибел, если . Отношение амплитуд, соответствующих мощностям и , отличаю­щихся на один децибел, означает, что

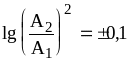, или ,

т.е. одному децибелу (дБ) соответствует . Так как мо­дуль АФХ определяет отношение амплитуд выходного и входного сигналов, то логарифмическая амплитудно-частотная характеристика (ЛАЧХ) строится в функции и представляет зависимость

.

При этом соответствует 100 дБ,

соответствует 80дБ и т.д.

соответствует -100 дБ.

Логарифмическая фазочастотная характеристика (ЛФЧХ) строится как и логарифмическая амплитудно-частотная характеристика (ЛАЧХ) в функции .

4.2 Типовые звенья САУ

По динамическим свойствам независимо от физической природы простейшие (неделимые) звенья подразделяются на усилительные (масштабные), апериодические, интегрирующие, дифференцирующие, ко­лебательные, звенья чистого запаздывания. На эти звенья можно разложить систему любой сложности, а также синтезировать из них желае­мую систему любой сложности.

Основными характеристиками звеньев являются: дифференциальное уравнение, передаточная и переходная функции, амплитудно-фазовая характеристика, логарифмические частотные характеристики (ЛАЧХ, ЛФЧХ).

Усилительные звенья

Особенностью усилительных звеньев является их практическая безынеционность, т.е. выходная величина в точности воспроизводит входную в измененном масштабе (усилители, потенциометры, редукто­ры, рычаги и т.д.):

, (4.4)

где - коэффициент усиления, который может быть больше и меньше единицы и иметь размерность, согласующую выходную и входную вели­чины.

В операторной форме (4.4) запишем так:

.

Передаточная функция усилительного звена:

.

Амплитудно-фазовая характеристика

не зависит от частоты.

На комплексной плоскости представляем точку на положительной вещественной оси, удаленную от начала координат за величину .

Если на вход звена подается ступенчатый единичный сигнал, то на выходе получается переходная функция в виде ступенчатого сигнала величины .

Логарифмическая амплитудно-частотная характеристика (ЛАЧХ) имеет вид прямой линии, параллельной оси абсцисс и удаленной от нее на расстоянии . Фазочастотная логарифмическая характеристика (ЛФЧХ) сливается с осью абсцисс. Поскольку отсутствует (равен нулю) сдвиг фаз между входным и выходным сигналами.

Апериодическое звено

Его называют инерционным звеном первого порядка, одноёмкостным статическим звеном. Дифференциальное уравнение его запишем так:

, (4.5)

где - постоянная времени, имеющая размерность времени, -коэффициент усиления.

В операторной форме (4.5) запишем так (при нулевых начальных условиях):

. (4.6)

Передаточная функция звена будет такой:

. (4.7)

Если , т.е. , то

,

откуда .

Используя метод неопределенных коэффициентов, получаем:

.

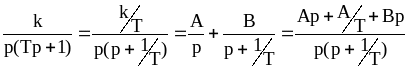Приравняв коэффициенты числителя при одинаковых степенях , получаем:

; .

Отсюда ; и

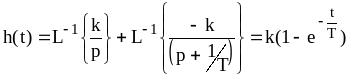. (4.8)

Сделав в передаточной функции (4.7) замену , получим:

.(4.9) 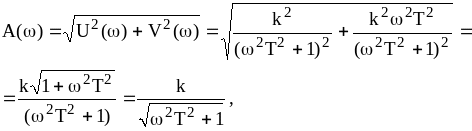(4.10)

где - амплитудно-частотная характеристика.

Фазо-частотная характеристика .

(4.11)

АФХ апериодического звена представляет окружность с центром на вещественной оси на расстоянии и радиусом . Действительно, ,

.

Отсюда . Это выражение можно записать так: .

Оно представляет окружность радиусом с центром на вещественной положительной оси на расстоянии от начала координат (рисунок 4.1).

Для построения ЛЧХ используем и .

.

При , и .

, , .

, ; .

ЛАЧХ и ЛФЧХ апериодического звена изображены на рисун- ке 4.2. На участке ЛАЧХ имеет отрицательный наклон, величина которого - . Для частот и значение будет равно:

дБ.

Интегрирующее звено

Выходная величина интегрирующего звена равна интегралу по времени от входной, , или

. (4.12)

В операторной форме выражение (4.12) запишем так:

, передаточная Функция звена равна:

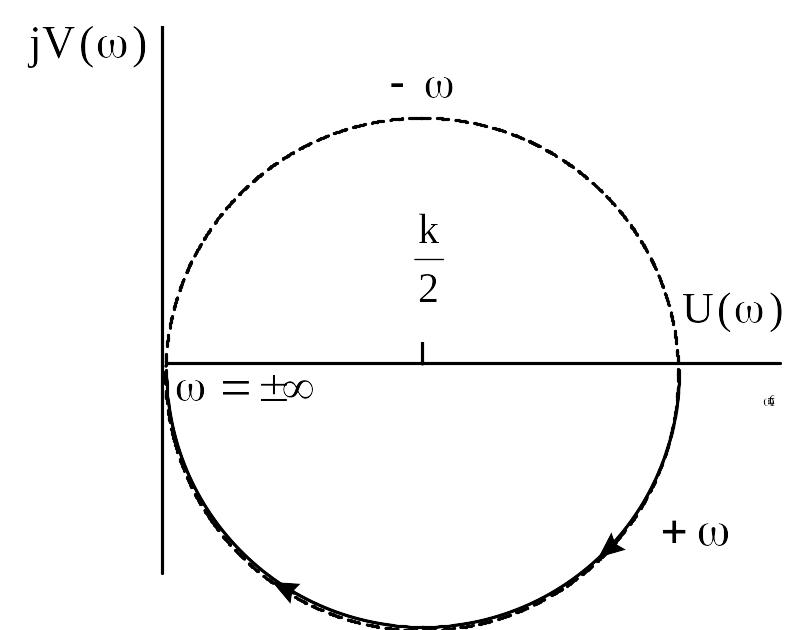
Рисунок 4.1 - АФХ апериодического звена

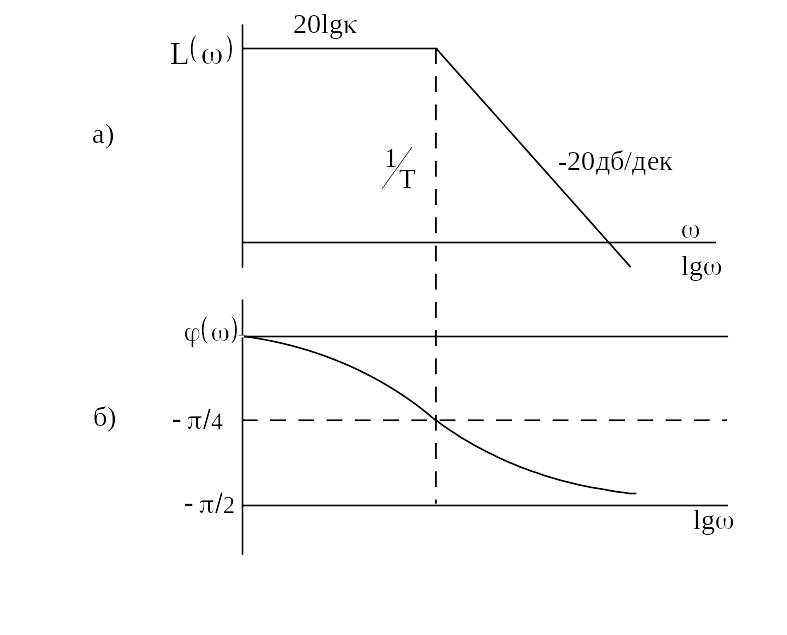
Рисунок 4.2 - Логарифмические характеристики апериодического звена

; . (4.13)

Решение уравнения (4.12) при нулевых начальных условиях и при единич­ном входном воздействии имеет вид:

, или , (4.14)

где - постоянная времени интегрирования, численно равна време­ни, через которое значение выходной величины станет равно входному воздействию (рисунок 4.3).

Амплитудно-Фазовая характеристика интегрирующего звена по­лучается из уравнения (4.12) заменой :

. (4.15)

Очевидно, что АФХ интегрирующего звена совпадает с мнимой осью комплексной плоскости, начинаясь в при и стремясь к нулю при .

ЛАЧХ представляет прямую, имеющую наклон -20 и проходящую через точку на оси абсцисс . ЛФЧХ, как это вид­но из выражения (4.15), не зависит от частоты и представляет собой прямую, параллельную оси абсцисс, удаленную от нее на величину .

Примерами интегрирующих звеньев могут служить гидравлический сервомотор, электрический двигатель постоянного тока, если выходной величиной является угол поворота, одноёмкостный объект без саморегулирования.

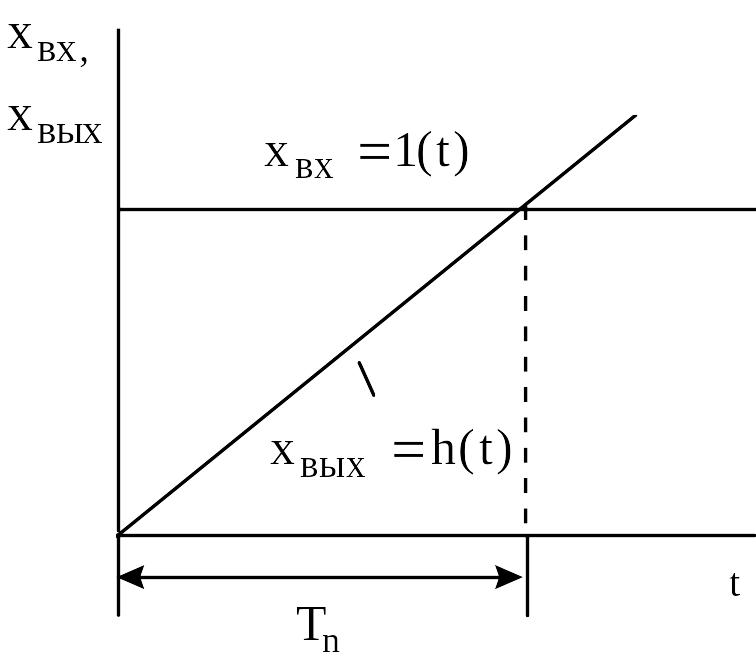
Рисунок 4.3 - Иллюстрация постоянной времени идеального интегрирующего звена

Дифференцирующее звено

Для идеального (физически не реализуемого) дифференцирующего звена выходная величина пропорциональна скорости изменения входной

, (4.16)

где - постоянная времени дифференцирования.

Переходная функция дифференцирующего звена представляет бесконечно большой амплитуды и бесконечно малой длительности импульс, площадь которого равна .

,

где при .

Передаточная и амплитудно-фазовая характеристики дифференцирующего звена получаются из выражения (4.16) и равны:

; . (4.18)

Легко видеть, что АФХ дифференцирующего звена совпадает с мнимой осью. Она начинается в начале координат при и устремляется в верхнюю полуплоскость при .

ЛАЧХ: . Это прямая с наклоном , ордината которой равна нулю при . ЛФЧХ есть прямая линия, параллельная оси абсцисс и проходящая от нее на расстоянии .

Колебательное звено

Статические и динамические свойства колебательного звена описываются дифференциальным уравнением второго порядка вида

, (4.19)

где , - постоянные времени, имеющие размерность времени. В операторном виде уравнение (4.19) запишем так:

, (4.20)

откуда передаточная функция

. (4.21)

Для получения переходной функции необходимо решить уравнение (4.19) при единичном входном воздействии. При этом решение будет зависеть от вида свободной составляющей, определяемой корням характеристического уравнения

, (4.22)

где .

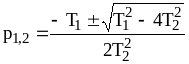Рассмотрим вид переходной функции для различных видов корней характеристического уравнения (4.22).

а) . В этом случае корни будут вещественными отрицательными, , . Вынужденная составляющая может быть найдена исходя из нового установившегося состояния, когда

. (4.23)

Полное решение уравнения (4.19) имеет вид

. (4.24)

Постоянные интегрирования и определяют по начальным условиям. При ступенчатом воздействии , равно нулю при . В противном случае , что невозможно, поскольку правая часть уравнения (4.19) конечна. Аналогично при , так как иначе равнялось бы бесконечности. Учитывая это обстоятельство, получим систему уравнений:

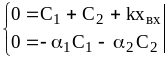, (4.25)

откуда ; .

Переходную функцию запишем так:

. (4.26)

б) . ,

. (4.27)

Для нулевых начальных условий, обоснование которых дано выше, имеем:

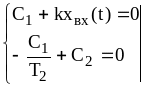, (4.28)

отсюда ; .

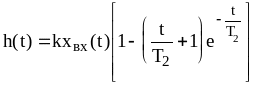. (4.29)

в) , где ; ,

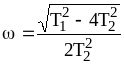. (4.30)

Постоянные интегрирования и найдем по нулевым начальным условиям ,

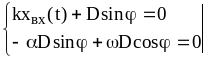, (4.31)

откуда ,

.

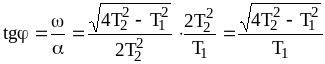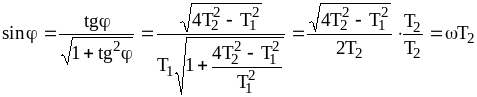. (4.32)

С учетом выражения (4.32) переходная функция принимает вид:

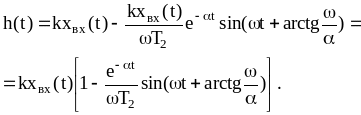
(4.33)

При условии инерционное звено второго порядка превращается в колебательное. Мнимая часть корней является круговой частотой колебаний, , где - период колебаний. Оценку переходного процесса в колебательном звене производят по степени затухания:

;

.

Степень затухания тем больше, чем больше отношение , и равна единице при . Если , то , при этом , и переходная функция (4.33) принимает вид:

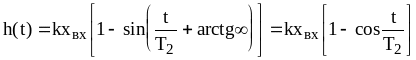. (4.34)

Амплитудно-фазовая характеристика колебательного звена получается из выражения (4.21) заменой :

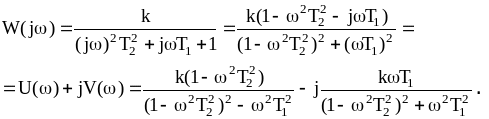
(4.35)

. (4.36)

. (4.37)

При АФХ колебательного звена, начинаясь на положительной вещественной полуоси комплексной плоскости, проходит 4-й и 3-й квадранты и приближается к началу координат при изменении .

Если корни характеристического уравнения вещественные отрицательные, то передаточную функцию (4.21) можно записать так:

. (4.38)

Это эквивалентно включению последовательно двух апериодических звеньев. Поскольку в процессе логарифмирования произведения результат равен сумме логарифмов сомножителей, то результирующая ЛАЧХ получается сложением ЛАЧХ отдельных апериодических звеньев. ЛФЧХ также получается сложением ЛФЧХ каждого из звеньев, поскольку при перемножении векторов их аргументы складываются. Примерный вид ЛАЧХ и ЛФЧХ инерционного звена второго порядка (апериодического) изображена на рисунке 4.4.

При комплексно-сопряженных корнях точное построение ЛАЧХ мо­жет быть произведено по АЧХ:

.

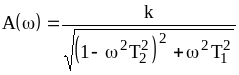При приближенном построении ЛАЧХ по двум асимптотам можно воспользоваться следующими рекомендациями:

при малых частотах ,

вторая асимптота, характеризующая высокочастотную составляю­щую, определяется так:

.

Примерный вид ЛАЧХ и ЛФЧХ при комплексно-сопряженных корнях изображен на рисунке 4.5.

Звено чистого запаздывания

Уравнение, связывающее выходную и входную величины:

. (4.39)

Передаточная функция звена

. (4.40)

Амплитудно-фазовая характеристик

. (4.41)

АФХ представляет на комплексной плоскости окружность единичного радиуса с центром в начале координат.

ЛАЧХ сливается с осью абсцисс, а ФЧХ есть линейная функция , проходящая через начало координат.

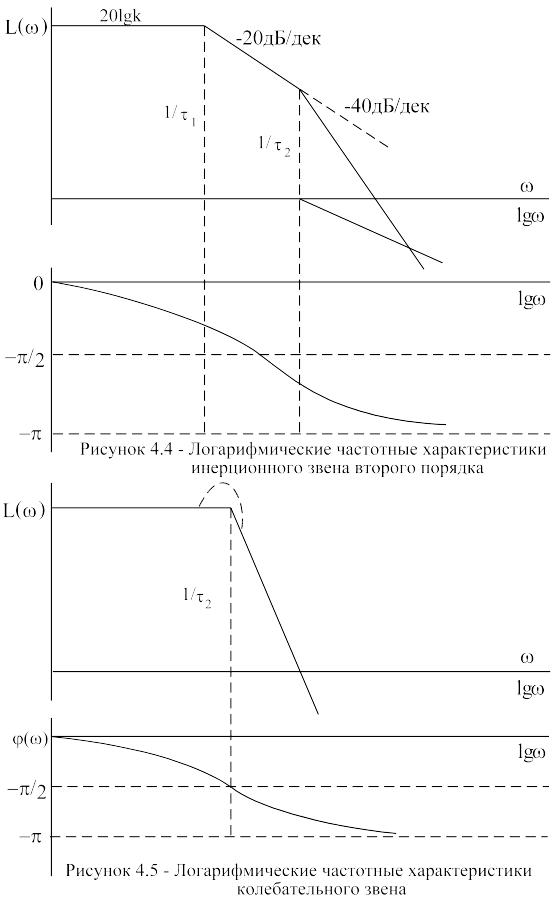
4.3 Основные законы регулирования

Будем считать, что на вход регулятора подается сигнал рассогласования между заданным и действительным значением регулируемой величины (рисунок 4.6):

. (4.42)

Кроме того, рассмотрим законы регулирования идеальных регуляторов, т.е. таких, какими стремятся их сделать. Однако конст­руктивные особенности, условия физической реализуемости, наличие промежуточных неидеальных звеньев приводят к появлению дополни­тельных балластных звеньев типа апериодических, искажающих желаемые свойства регулятора.

В настоящее время промышленные регуляторы реализуют следующие основные законы регулирования: П - пропорциональный, И - интегральный, ПИ - пропорционально-интегральный ПД - пропорционально-дифференциальный, ПИД - пропорционально – интегрально - дифференциальный.

Для идеального регулятора, реализующего П - закон регулирования справедливо соотношение

, (4.43)

где - неравномерность регулятора - то изменение регулируе­мой величины, которое обеспечивает полный ход регулирующего органа.

В реальном регуляторе это соотношение будет другим. Для выяснения причин отличия свойств реального регулятора от иде­ального рассмотрим динамику реального регулятора прямого действия (рисунок 4.7).

Регулятор температуры прямого действия

В качестве измерителя температуры в регуляторе используется термобаллон, заполненный легкокипящей жидкостью, которая испа­ряясь, повышает давление в термобаллоне. При этом по капилляру часть паров поймает в сильной, выполняющий роль исполнительного механизма, воздействующего на регулирующий орган, установленный на подаче теплоносителя (хладагента) (рисунок 4.7). При увеличе­нии температуры объекта давление в термобаллоне повышается, повышается давление в сильфоне, который перемещает шток регулирую­щего органа, уменьшая подачу теплоносителя. При снижении температуры объекта давление в сильфоне уменьшается, и шток регулирую­щего органа перемещается в противоположном направлении за счет пружины (жесткости самого сильфона) открывая подачу теплоносите­ля .

В общем случае зависимость между температурой жидкости в термобаллоне и парциальным давлением паров над ней нелинейная и может быть записана так:

. (4.44)

В линейном приближении эту зависимость в приращениях можно представить в виде:

(4.45)

где - частная производная в окрестности рабочей тем­пературы .

Зависимость в приращениях для перемещения штока регулирующе­го органа может быть записана так:

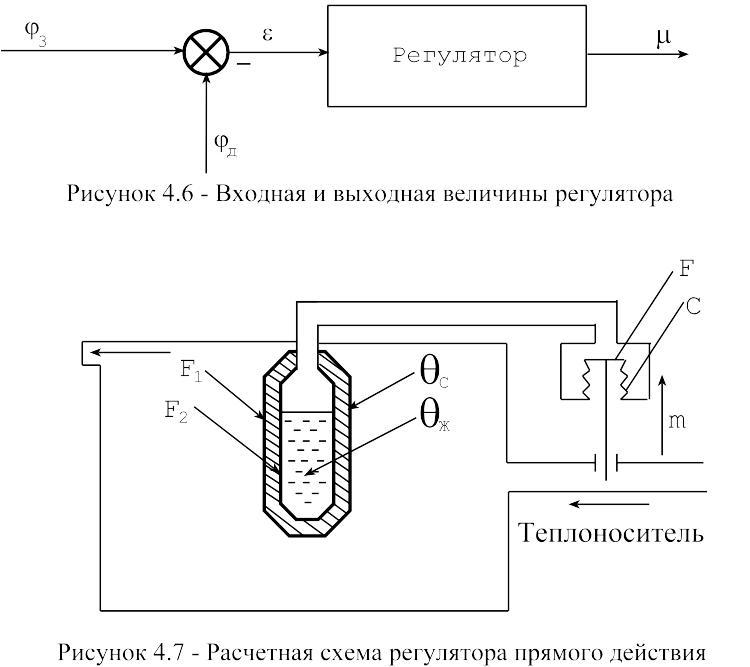
(4.46)

где - жесткость сильфона вместе с пружиной; - эффективная площадь сильфона; - усилие, действующее на шток регулирующего органа.

В соответствии с определением понятия неравномерности регулятора, для обеспечения полного хода регулирующего органа не­обходимо изменение температуры, равное . Поэтому выражение (4.46 ) запишем так:

(4.47)

Разделив зависимость (4.46) на выражение (4.47) получим

(4.48)

Запишем обозначения:

Тогда (4.48) принимает вид

(4.49)

Для выявления связи между регулируемой величиной - - температурой в аппарате и температурой жидкости в термобаллоне составим уравнение теплового баланса потока, идущго от из­меряемой среды объекта к стенке термобаллона , и от него к жидкости в термобаллоне . Для этого сделаем допущения: теп­лоемкости жидкости и стенки металла не зависят от температуры; коэффициенты теплоотдачи от жидкости к стенке и от стенки к жидкости постоянны; площади стенок термобаллона - наружная и внутренняя - постоянны, масса термобаллона и жидкости в термобаллоне - постоянны:

(4.50)

(4.51)

Для установившегося режима справедливо соотношение:

(4.52)

Текущие значения переменных можно представить так:

(4.53)

Если записать выражение (4.50) с учетом зависимости (4.53), а затем вычесть из него уравнение (4.52), то получим уравнение в приращениях:

(4.54)

Аналогично уравнение (4.51) можно записать в виде:

(4.55)

Из двух уравнений (4.54) и (4.55) необходимо исключить промежуточную переменную . Для этого разрешим уравнение (4.55) относительно :

(4.56)

Продифференцируем это выражение:

(4.57)

Подставим значения выражений (4.56) и (4.57) в уравнение (4.54), получим:

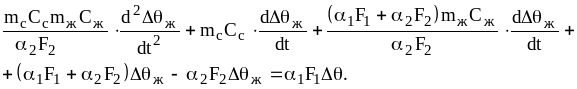
Сгруппировав слагаемые, получим

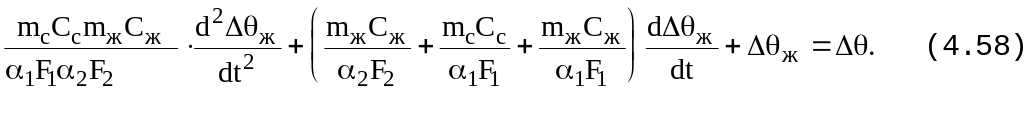Обозначим

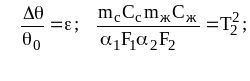
Коэффициенты имеют размерность времени.

Разделив все слагаемые на и учитывая выражение (4.49), окончательно получим

(4.59)

В установившемся режиме при имеем .

Если постоянные времени и малы по сравнению с постоянной времени объекта и ими можно пренебречь, то получаем вы­ражение (4.43). Знак минус указывает на то, что при увеличении регулируемой величины регулирующий орган закрывается. Неравномерность регулятора может быть абсолютной (в единицах регулируемой величины) и относительной (по отношению к максимальному или номинальному значению регулируемой величины). Величина, обратная неравномерности, называется коэффициентом усиления регуля­тора и представляет отношение приращения выходной величины к приращению входной в установившемся режиме.

(4.60)

Характеристики идеального пропорционального регулятора ана­логичны характеристикам усилительного звена.

Интегральный регулятор

Описывается уравнением

(4.61)

где - постоянная времени интегрирования, является настроеч­ным параметром регулятора. Характеристики его аналогичны характеристикам идеального интегрирующего звена.

Пропорционально-интегральный регулятор

Может быть реализован с независимыми параметрами настройки :

(4.62)

и с зависимыми:

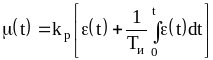. (4.63)

В случае (4.62) называется постоянной времени интегри­рования и есть время, через которое выходная величина за счет интегральной составляющей достигнет значения входного воздействия. Проинтегрировав (4.62), получим

.

При второе слагаемое равно , т.е. входной величине.

В случае (4.63) называется временем изодрома или временем удвоения. Проинтегрировав (4.63), получим

.

При второе слагаемое, получаемое за счет интегральной составляющей, достигает значения выходной величины, получаемой за счет пропорциональности составляющей, а на выходе регулятора результирующий сигнал удваивается.

Записав выражения (4.62) и (4.63) в операторной форме, легко получить передаточную функцию регулятора:

или из выражения (4.63):

(4.64)

В дальнейшем рассмотрим свойства ПИ-регулятора, имеющего передаточную функцию вида (4.64). АФХ регулятора:

(4.65)

где .

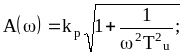
АФХ регулятора изображена на рисунке 4.8.

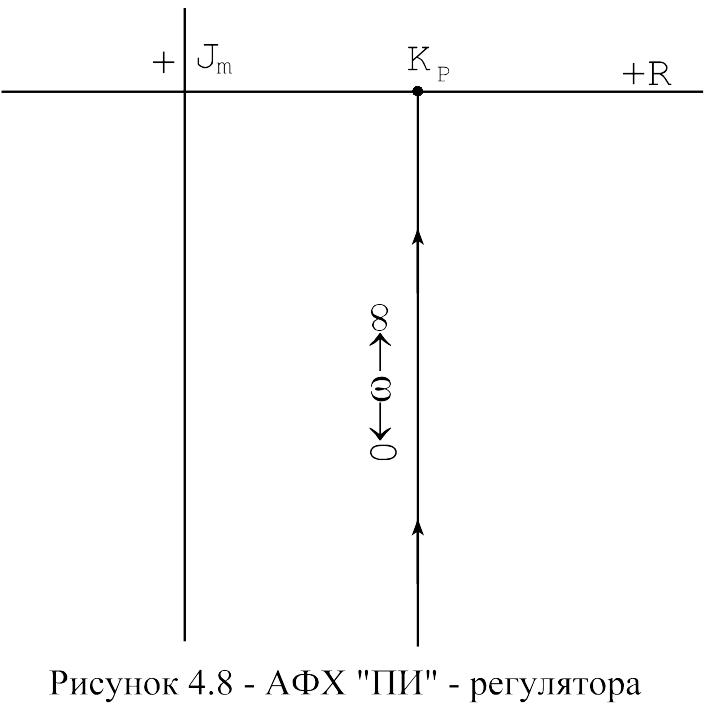
Логарифмическая амплитудно-частотная и фазочастотная характеристики получаются из выражения(4.65):

При Так как ,

второе слагаемое будет положительным и тем больше, чем меньше .

При , т.к. .

ЛАЧХ и ЛФЧХ изодромного регулятора изображены на рисунке 4.9.

При , т.е. коэффициент усиления САУ, равен , и статическая ошибка ее оказывается равной нулю.

Пропорционально-дифференциальный регулятор

Связь выходной и входной величин определяется соотношением

(4.66)

где - постоянная времени дифференцирования.

Передаточная функция имеет вид

(4.67)

Амплитудно-фазовая характеристика

(4.68)

На комплексной плоскости представляет прямую, начинающуюся на положительной вещественной оси на расстоянии и проходящую параллельно мнимой оси в первом квадранте.

Логарифмическая АЧХ:

(4.69)

При при

Графики ЛАЧХ и ФЧХ ПД-регулятора изображены на рисунке 4.10. На высоких частотах коэффициент усиления регулятора увеличивается, что обеспечивает повышение его быстродействия. Управляющее воздействие появляется даже при отсутствии отклонения, но при наличии тенденции к отклонению регулируемой величины.

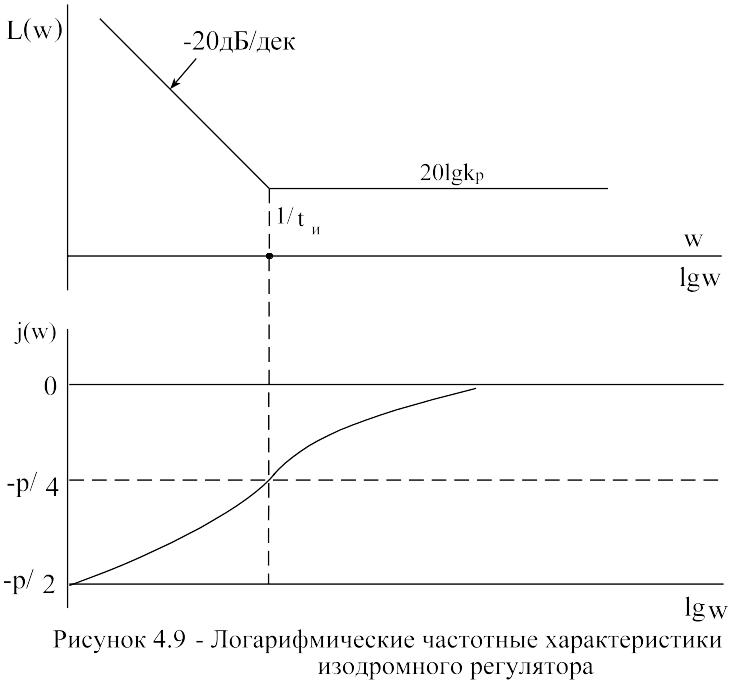
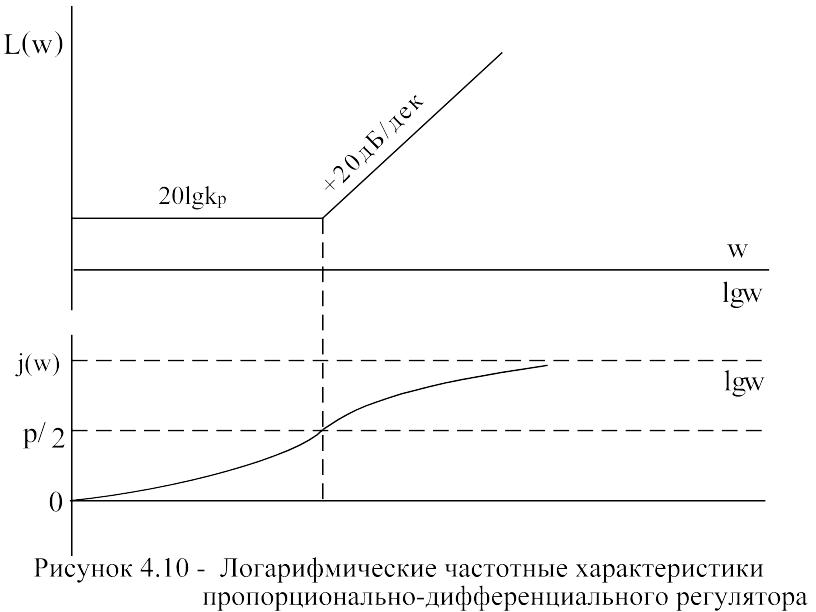
Пропорционально -интегрально-дифференциальный регулятор

Имеет три параметра настройки: изменяемые в определенном диапазоне. Связь выходной величины регулятора с входной такая:

(4.70)

Записав (4.70) в операторной форме и взяв отношение выходной величины к входной при нулевых начальных условиях, получим передаточную функцию регулятора:

. (4.71)

Амплитудно-фазовая характеристика (АФХ):

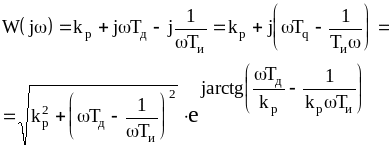
. (4.72)

ЛАФХ может быть представлена тремя характерными участками:

при преобладает интегральная составляющая и

при преобладает дифференциальная составляющая

при

Как следует из ЛАЧХ, ПИД - регулятор соединяет положительные свойства «ПИ» и «ПД»-регуляторов. Благодаря интегральной составляющей исключается статическая ошибка, а благодаря наличию производной в законе регулирования увеличивается коэффициент усиления регулятора на высоких частотах, что повышает его быстродействие.

5 УСТОЙЧИВОСТЬ СИСТЕМ УПРАВЛЕНИЯ

5.1 Общие положения об устойчивости

Система автоматического управления будет называться устойчивой, если выведенная из состояния равновесия и предоставленная самой себе она возвращается в исходное состояние, т.е. при снятии внешнего воздействия САУ возвращается в то состояние, в котором она находилась до возмущения.

Известно, что вид переходного процесса в САУ определяется суммой двух составляющих - свободной и вынужденной. Поскольку вынужденная составляющая определяется внешним воздействием, а устойчивость линейной САУ зависит от ее поведения после снятия внешнего возмущения, то можно сделать следующий вывод: устойчивость линейной САУ не зависит от внешнего воздействия, а определяется видом свободной составляющей переходного процесса.

Свободная составляющая переходного процесса находит-ся как общее решение линейного однородного уравнения

, (5.1)

где - отклонение регулируемой величины от исходного установившегося состояния.

Поскольку решение уравнения (5.1) определяется корнями характеристического уравнения

, (5.2)

то, следовательно, устойчивость САУ будет зависеть от вида корней уравнения (5.2).

В случае различных вещественных корней

. (5.3)

Система автоматического управления будет устойчива, если

При ; нейтральна, если при ; неустойчива, если при .

Свободная составляющая будет стремиться к нулю тогда, когда каждое слагаемое суммы (5.3) будет стремиться к нулю при . Это условие будет выполняться в таких случаях:

все корни характеристического уравнения (5.2) отрицательные;

все корни имеют отрицательные вещественные части.

Если в характеристическом уравнении (5.2) будет хотя

бы один нулевой или пара мнимых сопряжений корней, то появятся слагаемые в выражении (5.3) вида , или которые не уменьшаются до нуля при и, следовательно, система будет нейтральна (находится на границе устойчивости). Если в уравнении (5.2) имеется мнимый или комплексный корень, то обязательно будет и сопряженный ему, поскольку все коэффиценты характеристического уравнения-вещественные числа, имеющие размерность , и т.д.

Если хотя бы один корень характеристического уравне-

ния САУ вещественный-положительный или пара комплексно-

-сопряженных корней имеет положительные вещественные час-

ти, то САУ неустойчива.

Характеристическое уравнение (5.2) можно записать в виде

(5.4)

где - корни характеристического уравнения (5.2). Если все корни (5.2) вещественные - отрицателные, то все множители (5.4) положительны, и, следовательно, в характеристическом уравнении (5.2) не может быть коэффициента с отрицательным знаком. Если то , и опять в характеристичес-ком уравнении (5.2) не может появиться отрицателный коэффицент. Следовательно, необходимым условием устойчивости САУ является наличие и положительность всех коэффицентов характеристического уравнения (если они все отрицательны, то можно поменять знак). Это условие необходимое, но не достаточное. Если оно выполняется, то имеет смысл искать и проверять достаточное условие -отрицательность вещественных частей всех корней характеристического уравнения. Однако для характеристического уравнения, степень которого выше 4-го порядка, нет точных формул для определения корней.

Решение уравнений даже 3-й степени с использованием формулы Кордано вызывает затруднения, для уравнений 4-й степени формулы еще более громоздки.

В настоящее время корни характеристического уравнения могут быть найдены на ЭВМ приближенными методами, однако не всегда под рукой есть ЭВМ. Поэтому исследователи искали косвенные методы (критерии) отрицательности вещественных частей корней характеристического уравнения. Еще в 1895 году по предложению словацкого профессора А.Стодолы немецкий математик Гурвиц предложил критерий, позволяющий не решая характеристического уравнения, определить отрицателность вещественных частей его корней, т.е. устойчивость САУ. Кроме того, критерий позволяет в общем виде находить соотношения между коэффициентами характеристического уравнения, обеспечивающие устойчивость системы управления, что само по себе очень важно.

5.2 Алгебраический критерий устойчивости Гурвица

Приводится без доказательства. Если характеристическое уравнение САУ имеет вид (5.2), то система автоматического управления будет устойчива, если при будут положительны все главные диагональные миноры определителя Гурвица до порядка.

Определитель Гурвица составляется следующим образом: по диагонали записывают коэффициенты от до , над диагональю записывают коэффициенты с возрастающим индексом, под диагональю - с убывающим, недостающие коэффициенты заменяются нулями. Например, для системы, имеющей характеристическое уравнение 4-й степени, получим

. (5.5)

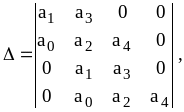
Поскольку , то при соблюдении необходимого условия устойчивости (положительность всех коэффициентов) достаточно чтобы положительными были диагональный минор. Очевидным является также утверждение, что при будет иметь место нулевой корень характеристического уравнения, т.е. система будет находиться на границе устойчивости. Если , а , то в характеристическом уравнении будут чисто мнимые корни, и она также будет на границе устойчивости. При этом все главные диагональные миноры до порядка должны быть положительными.

Критерий Гурвица удобен для исследования систем с характеристическим уравнением невысокой степени (до пятой). При высокой степени характеристического уравнения или при наличии звена чистого запаздывания, когда характеристическое уравнение становится трансцендентным из-за члена вида , удобнее, а при трансцендентном характеристическом уравнении единственно возможным, являются частотные критерии, обладающие простой геометрической интерпретацией.

5.3 Частотный критерий устойчивости Михайлова

Если в характеристическом уравнении (5.4), (5.2) положить , то получим годограф Михайлова

(5.6)

Найдем угол поворота элементарного вектора при изменении  от до (рисунок 5.1). При этом могут быть два случая: корень находится в левой полуплоскости комплексной плоскости, т.е. имеет отрицательную вещественную часть; корень находится в правой полуплоскости комплексной плоскости.

Если корень в левой полуплоскости, то при вектор направлен вниз. При увеличении вектор поворачивается против часовой стрелки ( в положительном направлении ) и при направлен вверх, т.е.

Если корень находится в правой полуплоскости, то вектор повернется аналогично предыдущему случаю только по часовой стрелке, т.е.

Вектор представляет произведение элементарных векторов (5.6), поэтому, если все корни характеристического уравнения (5.2) находятся в левой полуплоскости комплексной полуплоскости, т.е. САУ устойчива, то

Из выражения (5.6) следует, что

(5.7)

где

Вещественная часть равна есть частная функция , поэтому ветвь , построенная при изменении от до 0, будет симметрична ветви при изменении от 0 до . Поэтому нет смысла изменять от до достаточно построить при изменении от 0 до . При этом приращение аргумента будет в два раза меньше. Если САУ имеет характеристическое уравнение, корни которого находятся в левой полуплоскости, то

Поскольку необходимое условие требует положительности и наличия всех коэффициентов характеристического уравнения, то для устойчивой САУ .

САУ будет устойчива, если годограф Михайлова, начинаясь на положительной вещественной полуоси, последовательно проходит в положительном направлении (против часовой стрелки) " " квадрантов при изменении от 0 до ,

где - степень характеристического уравнения.

Рисунок 5.1 - Вращение элементарных векторов

Годограф Михайлова для устойчивых САУ при изображены на рисунке 5.2. Если годограф Михайлова проходит через начало координат, то САУ находится на границе устойчивости. При этом, если он начинается с нуля, то это указывает на наличие нулевого корня, если годограф начинается на положительной вещественной полуоси, но затем проходит через начало координат, то это значит имеются мнимые корни в характеристическом уравнении.

Если годограф Михайлова непоследовательно проходит квадранты комплексной плоскости или проходит не " " квадрантов, то САУ неустойчива.

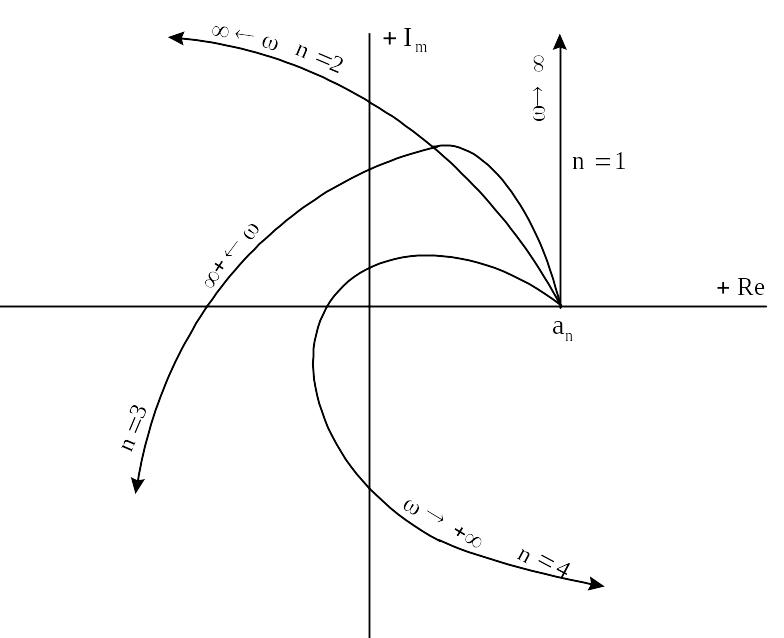
Рисунок 5.2 - Виды годографов Михайлова

Пусть характеристическое уравнение n-й степени имеет m корней в правой полуплоскости. Тогда

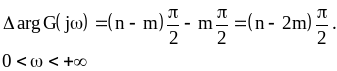
Итак, критерий устойчивости Михайлова позволяет не только анализировать устойчивость замкнутых и разомкнутых САУ, но и находить число неустойчивых корней

.

Для устойчивой САУ очевидным является свойство чередуемости и вещественности корней и .

5.4 Критерий устойчивости Найквиста - Михайлова

С помощью критерия устойчивости Найквиста-Михайлова по стационарным свойствам разомкнутой САУ можно судить о нестационарных свойствах замкнутой. Этот критерий был впервые предложен американским ученым Найквистом в 1932г. для анализа устойчивости радиоэлектронных устройств. А.В.Михайлов обобщил его и использовал впервые для анализа устойчивости систем автоматического управления.

Известно, что характеристическое уравнение замкнутой САУ, определяющее ее устойчивость, получается приравниванием нулю знаменателя передаточной функции замкнутой системы, т.е. .

Обозначим тогда

(5.8)

Если в выражении (5.8) заменить на , то в числителе получим годограф Михайлова для замкнутой системы, а в знаменателе - для разомкнутой. При этом степень числителя и знаменателя будут одинаковы и, если замкнутая и разомкнутая системы устойчивы, то

.

На комплексной плоскости это обозначает, что вектор при изменении от 0 до не поворачивается вокруг точки , или что вектор не охватывает на комплексной плоскости точку при изменении от 0 до (рисунок 5.3).

Таким образом, если разомкнутая САУ устойчива и ее АФХ не охватывает на комплексной плоскости точку с координатами , то замкнутая САУ будет устойчива.

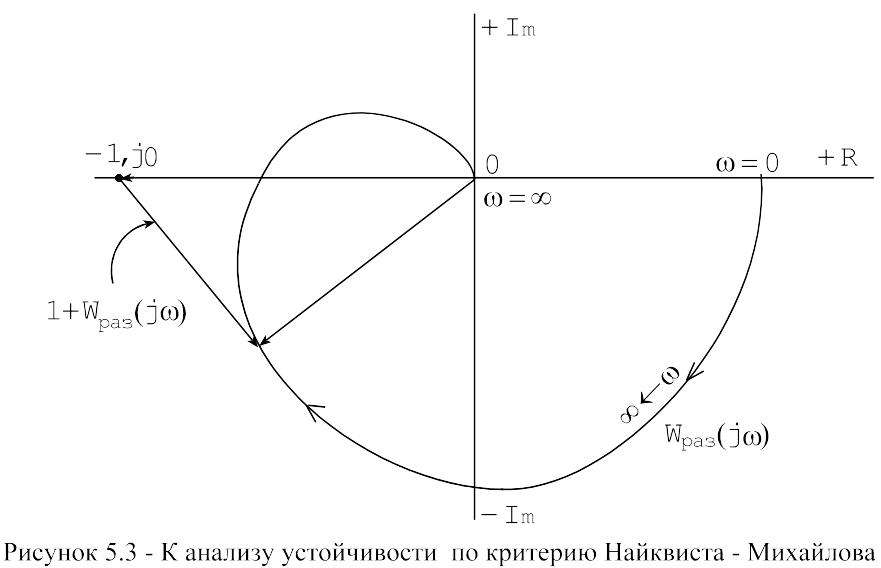
Если разомкнутая САУ неустойчива и имеет неустойчивых корней, а замкнутая САУ устойчива, то

Таким образом, если разомкнутая САУ неустойчива и имеет неустойчивых корней, то для устойчивости САУ в замкнутом состоянии необходимо, чтобы АФХ разомкнутой системы охватывала в положительном направлении точку на комплексной плоскости с координатами раз.

Если разомкнутая САУ неустойчива, то число неустойчивых корней можно определить по критерию Михайлова.

В том случае, если разомкнутая САУ находиться на границе устойчивости благодаря наличию нулевых корней, передаточную функцию ее можно записать так:

(5.9)

где - кратность нулевого корня.

При малых значениях АФХ нейтральной системы можно представить так:

(5.10)

где

Из выражения (5.10) следует, что при малых  значение . АФХ разомкнутой системы стремиться к началу координат при увеличении  по одной из осей координат комплексной плоскости:

при т.е. АФХ перемещается по отрицательной мнимой оси;

при т.е. АФХ перемещается по отрицательной вещественной оси;

при т.е. АФХ перемещается по положительной мнимой оси.

Для анализа устойчивости таких систем справедлив критерий устойчивости Найквиста-Михайлова, если их АФХ дополнить частью окружности бесконечного радиуса, которая

начинается на положительной вещественной полуоси, как это показано на рисунке 5.4.

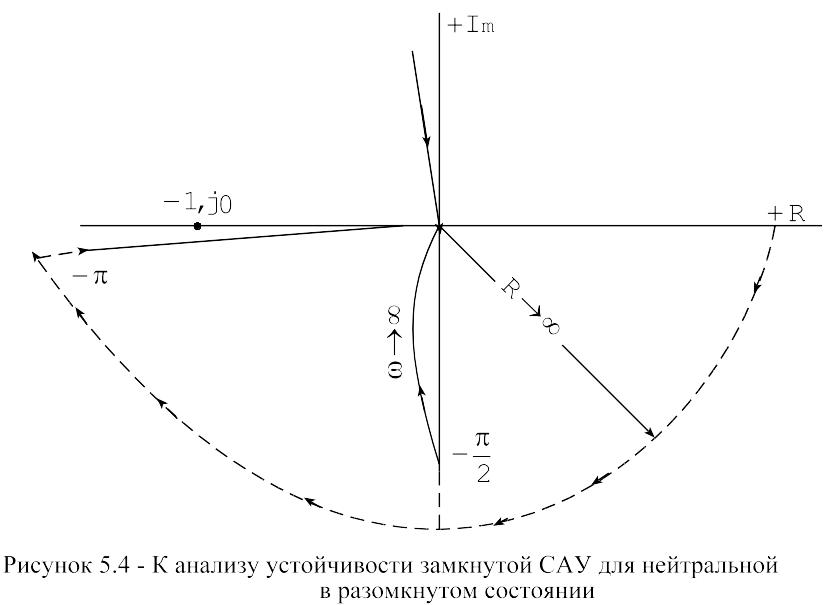
Из рисунка следует, что абсолютная устойчивость (устойчивость, которая не нарушается при уменьшении коэффициента усиления разомкнутой системы) может быть получена только при . При может быть получена только условная устойчивость.

5.5 Устойчивость САУ с запаздыванием

Если САУ имеет чистое запаздывание, то ее устойчивость можно определить только по критерию Найквиста-Михайлова, поскольку характеристическое уравнение будет иметь бесконечное множество корней из-за наличия сомножителя , делающего его трансцендентным.

Действительно, пусть .

Тогда характеристическое уравнение замкнутой системы будет

Раскладывая функцию в степенной ряд, получаем:

Перемножив члены ряда на , получим характеристическое уравнение степени «k», где k, что и требовалось доказать.

Систему с чистым запаздыванием можно рассматривать как предельную систему без запаздывания и звена чистого запаздывания, включенного последовательно:

(5.11)

Из выражения (5.11) следует, что наличие чистого запаздывания не изменяет амплитудно-частотную характеристику, модуль АФХ остается прежним, но изменяется фаза векторов - каждый из них поворачивается по часовой стрелке на угол . Поскольку значения модуля АФХ, как правило, больше при малых частотах, то наличие чистого запаздывания приводит к «разбуханию» АФХ, и она может охватить на комплексной плоскости точку с координатами .

Для определения критического значения , при котором САУ еще устойчива, проводят из начала координат комплексной плоскости единичным радиусом окружность. Точка пересечения ее с АФХ характеризует частоту , при которой Зная , можно найти 

(рисунок 5.5).

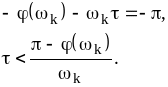(5.12)

Построив АФХ разомкнутой САУ, можно найти запас устойчивости замкнутой САУ по модулю и по фазе (рисунок 5.5,б). Запас устойчивости по фазе есть угол . Запас устойчивости по модулю иногда определяют по расстоянию от точки пересечения АФХ с отрицательной вещественной осью до минус единицы, иногда как величину , где - расстояние от точки пересечения АФХ с отрицательной вещественной осью до начала координат.

5.6 Логарифмический частотный критерий устойчивости

Исследование устойчивости САУ существенно упрощается при применении ЛЧХ благодаря простоте построения ЛЧХ и очевидной связи параметров системы с видом этих характеристик, что не только дает возможность видеть влияние того или иного параметра на устойчивость, но и определять характеристику корректирующего звена, обеспечивающего требуемые показатели качества САУ.

Если разомкнутая САУ устойчива, то замкнутая САУ также будет устойчива, если ордината логарифмической фазочастотной характеристики на частоте среза ( - частота, при которой ) системы по абсолютной величине меньше , т.е. (рисунок 5.6.). На рисунке изображены для 1)-устойчивой; 2)-на границе устойчивости; 3)- неустойчивой систем.

Считается, что система обладает достаточным запасом устойчивости по фазе, если и по модулю, если

Запас устойчивости по амплитуде определяется как число децибел, на которое нужно увеличить усиление системы, чтобы она достигла границы устойчивости.

Для систем, обладающих более сложной формой АФХ, удобнее для анализа устойчивости пользоваться формулировкой, вытекающей из правила определения числа переходов ЛЧФХ через линию .

Переход ЛЧФХ линии снизу вверх считается положительным, сверху вниз - отрицательным.

Система, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом, если разность положительных и отрицательных переходов ЛФЧХ линии равна нулю в диапазоне частот, в котором ЛАЧХ положительна (рисунок 5.7).

Для АФХ это эквивалентно четному числу пересечений отрезка отрицательной вещественно оси , т.е. отсутствию охвата точки на комплексной плоскости с координата-

ми .

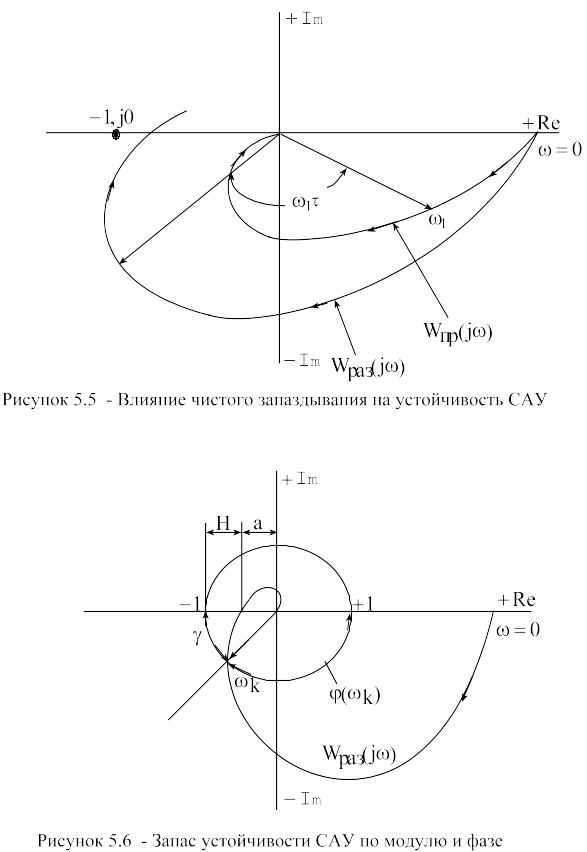
Таким образом, количественными оценками запаса устойчивости систем управления являются: запас устойчивости по модулю и запас устойчивости по фазе. Наличие двух параметров оценки качества усложняет задачу оптимизации систем управления. Как выходят из положения в этом случае, будет описано ниже.

6 АНАЛИЗ ЛИНЕЙНЫХ САУ

6.1 Структурные преобразования САУ

При анализе САУ любой сложности приходится изменять ее структуру не изменяя свойств в целях удобства исследования или наглядности, необходимости моделирования или выбора корректирующих звеньев. При этом следует пользоваться следующими очевидными правилами:

при последовательном включении звеньев их результирующая передаточная функция равна произведению передаточных функций от­дельных звеньев;

при параллельном включении звеньев результирующая переда­точная функция равна сумме передаточных функций отдельных звеньев;

при встречно-параллельном включении звеньев результирующая передаточная функция равна частному от деления передаточной функции прямой связи на единицу плюс или минус передаточная функ­ция разомкнутого контура, в котором звенья включены встречно-параллельно (рисунок 6.1). При этом знак «плюс» соответствует отрица­тельной, а «минус» - положительной обратной связи. Для схемы (рисунок 6.1) справедливы соотношения: .

Исключив из этой системы уравнений промежуточные переменные и , получим : . (6.1)

При последовательном соединении минимально фазовых звеньев результирующая передаточной функции будет также минимально фа­зовой.

При параллельном соединении звеньев сумма минимально фазовых звеньев может иметь нули в правой полуплоскости и, следователь­но, дать неминимально-фазовое звено. И наоборот, параллельное соединение не минимально фазовых звеньев может дать минимально фазовое звено.

При перемещении звена через узел по направлению ветвления необходимо в подсоединенные к узлу ветви добавить звенья с передаточной функцией перемещаемого звена (рисунок 6.2).

При перемещении звена через узел ветвления против направления ветвления необходимо в подсоединенные к узлу ветви доба­вить звенья с передаточной функцией, обратной передаточной функции перемещаемого звена (рисунок 6.3).

На (рисунке 6.2) и (рисунке 6.3) короткие верхние стрелки указывают нап­равление ветвления, нижние длинные - направление переноса зве­на.

В 1953 г. Мейсон предложил формулу для вычисления передаточ­ной функции системы любой сложности между любыми двумя переменными. Для этого ее представляют в форме сигнальных графов, состоящих из узлов и вершин. Точки, где новые сигналы не образуются, узлами не являются. Ветвями являются передаточные функции. Передаточная функция ветви обратной связи имеет знак этой связи. Изображения сигналов, входящих в какой-либо узел, складываются, образуя изображение нового сигнала, выходящего из этого узла (рисунок 6.4). Результирующая передаточная

функция определяется по формуле: . (6.2)

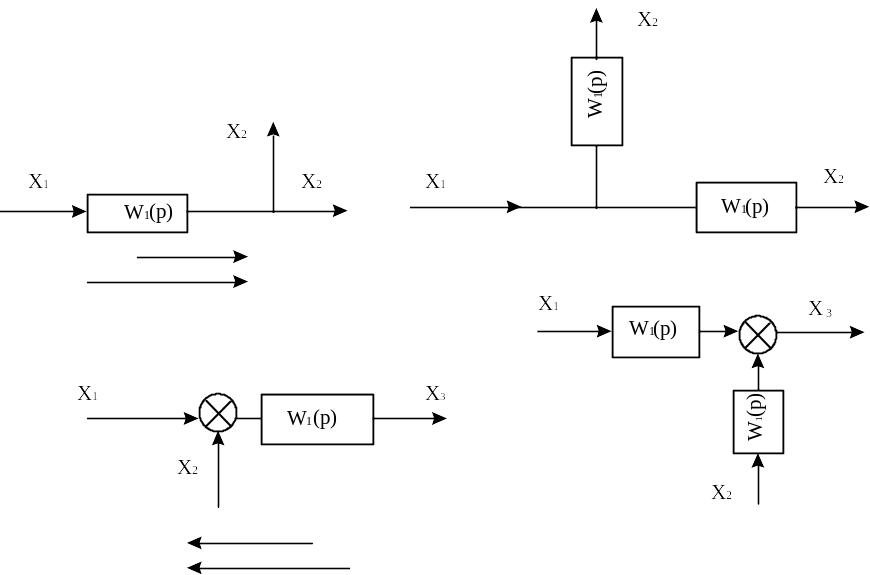
Рисунок 6.2 - Виды переноса ветвлений

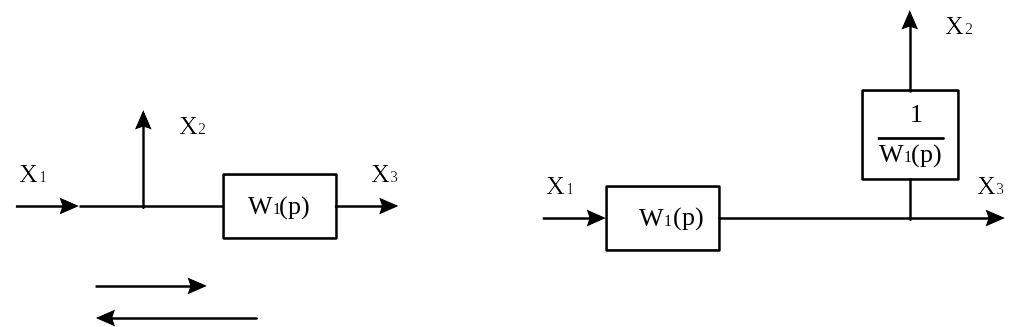
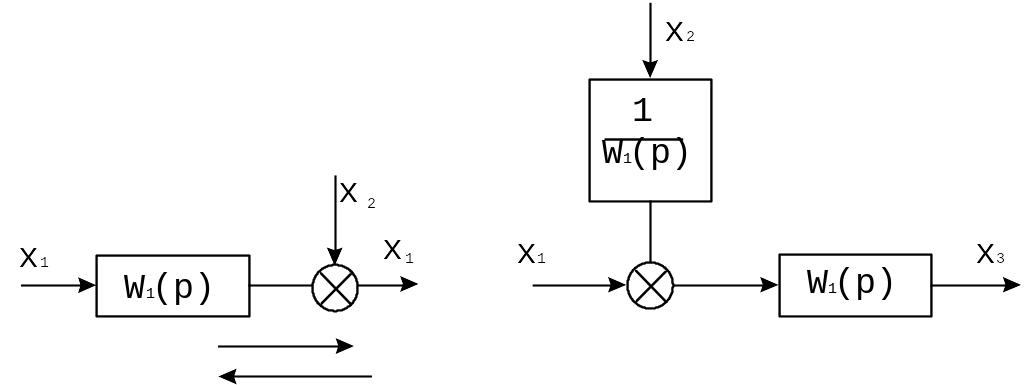
Рисунок 6.3 - Виды переноса звеньев

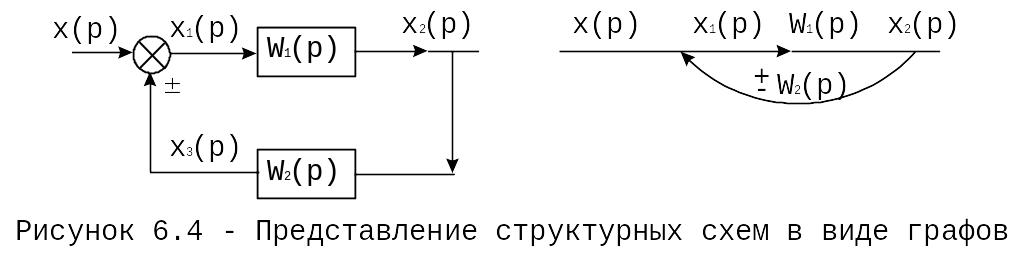
Здесь -передаточная функция -го пути, составленная без учета имеющихся в ней обратных связей, т.е. произведения передаточ­ных функций ветвей сигнального графа, образующего этот путь;

- определитель сигнального графа системы;

- адъюнкт -го прямого пути.

и выражаются через передаточные функции контуров, состоя­щих из ветвей, образующих замкнутый путь прохождения сигнала. Контуры называются не касающимися, если они не содержат общих уз­лов.

равен единице минус сумма произведений передаточных Функ­ций всех возможных сочетаний по нечетным числам не касающихся контуров, плюс сумма произведений передаточных функций всех возможных сочетаний по четным числам не касающихся контуров. В сум­му членов, содержащих передаточные функции по одному контуру, входят передаточные функции всех замкнутых контуров.

составляется таким же образом для той части системы, которая не касается i-го прямого пути, т.е. не имеет с ним общих узлов.

Проиллюстрируем сказанное примером для сигнального графа, изображенного на (рисунке 6.5). Опустим аргумент передаточных функ­ций в целях упрощения записи. Прямых путей от к шесть:

Имеется два некасающихся контура:

и и еще контур .

В соответствии с определением:

Для остальных путей не касающихся контуров нет, поэтому

.

Пользуясь формулой (6.2), определяют результирующую передаточную функцию.

Применение уравнения (6.2) существенно усложняется, если существуют все возможные связи между узлами графа. При этом возникает необходимость введения некоторых дополнительных понятий и применения ветвящихся диаграмм которые мы рассматри­вать не будем.