38. Правило Лопиталя.
Теорема (правило Лопиталя). Пусть А – число, символ одностороннего предела (А=а±0) или символ бесконечности (А=±∞). Пусть функции ƒ(х) и g(х) либо обе бесконечно малые, либо обе бесконечно большие при х→А. Тогда, если существует предел
(
конечный
или бесконечный),
то существует и предел
при этом выполняется равенство:
39. Производные и дифференциалы высших порядков.
Если для функции y=f(x) определена производная у(к-1) порядка (к-1), то производную у(к) порядка к (при условии ее существования) определяют как производную от производной порядка (к-1), т.е. у(к) = (у(к-1))′ . В частности, у’’=(y’)’- производная второго порядка, y’’’=(y’’)’ – третьего и т.д.
Дифференциалы высших порядков ф-и y=f(v) последовательно определяются таким образом:
d2y=d(dy) – диф-л 2-го порядка
d3y=d(d2y)…
dny=d(d n-1 y) - диф-л n-го порядка
40. Формула Тейлора. Формула Маклорена.
теорема Тейлора.
Пусть
функция f(x) имеет в точке x = a и
некоторой ее окрестности производные
порядка n+1. Тогда между точками a и
x a найдется такая точка
,
что справедлива следующая формула:
|
|
Формула (10) называется формулой Тейлора, а выражение
представляет остаточный член в форме Лагранжа. Заметим, что если функция f(n+1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a)n. Таким образом, остаточный член можно записать в виде
Rn+1(x) = o((x-a)n) при x a.
Данная форма записи остаточного члена называется формой Пеано.
Формулой Маклорена называется формула Тейлора при a = 0:
|
|
Остаточный член в форме Пеано для формулы Маклорена имеет вид
Rn+1 = o(xn) при x 0.
П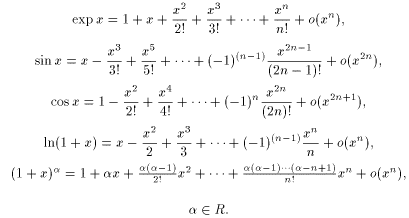
риведем
разложения некоторых элементарных
функций по формуле
Маклорена
Найдите, исходя из
определения, производную функции f(x) в точке x0:
26. f(x) = x3, x0 - произвольное число.
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
f(x) = x3
f
′(xо)=
=
=
=
=3
27. f(x)=sinx, xо-произвольное число
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f ’(x)= =
f
′(xо)=
=
=
=cosx0
28.
f(x)=
,
xо
=9
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f ’(x)= =
f
’(x)=
=
=
=1/6
29.
f(x)=
,
xо
=1
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f ’(x)= =
f
’(x)=
=
=
=
=-2
30. f(x)=xx, x0=0
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f
’(x)=
=
31.
Производной функции f(x) в точке x0 называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего произвольным образом к 0.
f ’(x)= =
Найдите эластичность функции f (x) в точке x0:
38. f(x) = x4 , x0 = 9.
Эластичностью
функции y
= f(x)
в точке х0
называется предел
f
(x) = x4 =>
E(x)=
,
при x0
= 9.
39. f(x) = 3x , x0 = 5.
Эластичностью функции y = f(x) в точке х0 называется предел
E(x)=
