11.1.4. Диверсификация

Рассматривая N бумаг, мы получим:

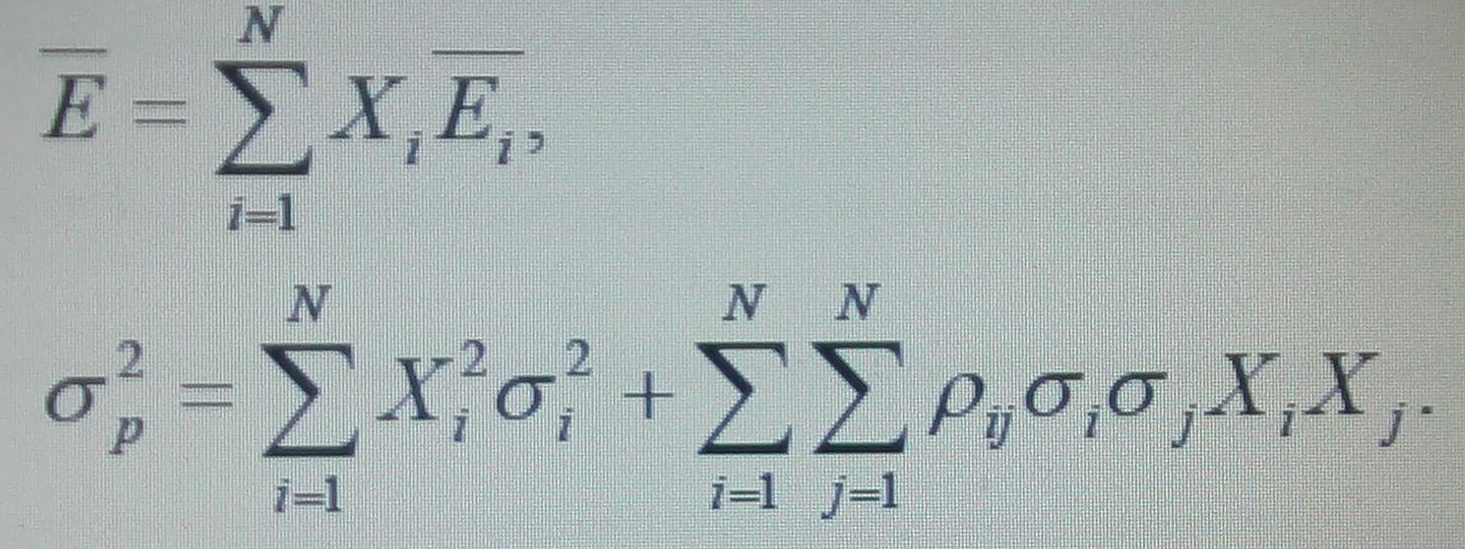
Пусть 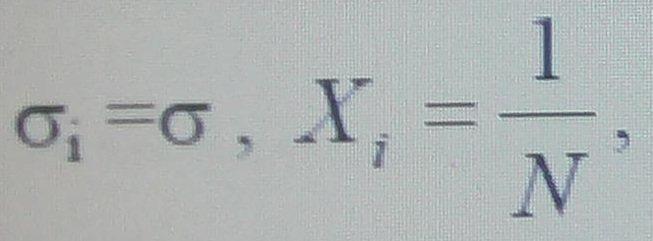тогда

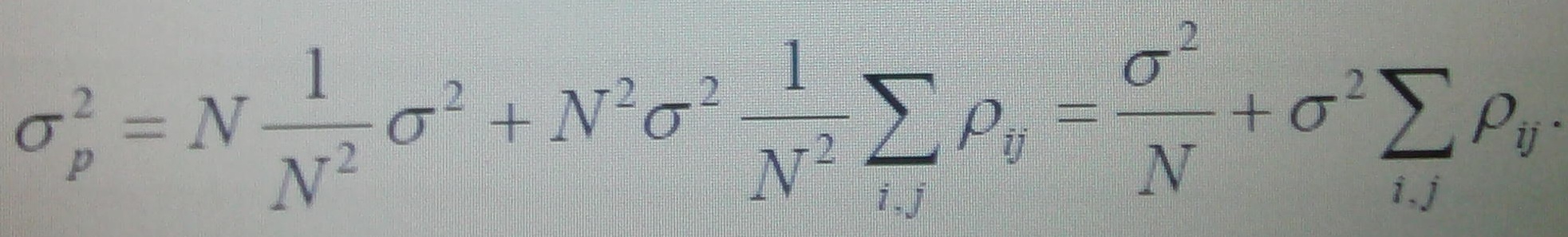
Как видите, при N → ∞ первое слагаемое → 0.

Таким образом, чем больше число акций в портфеле, тем меньше его вариация и, следовательно, риск. Первое слагаемое называется уникальным риском; второе — систематическим риском и принципиально не исчезает ни при каком составе портфеля. Увеличение числа акций в портфеле называется диверсификацией.

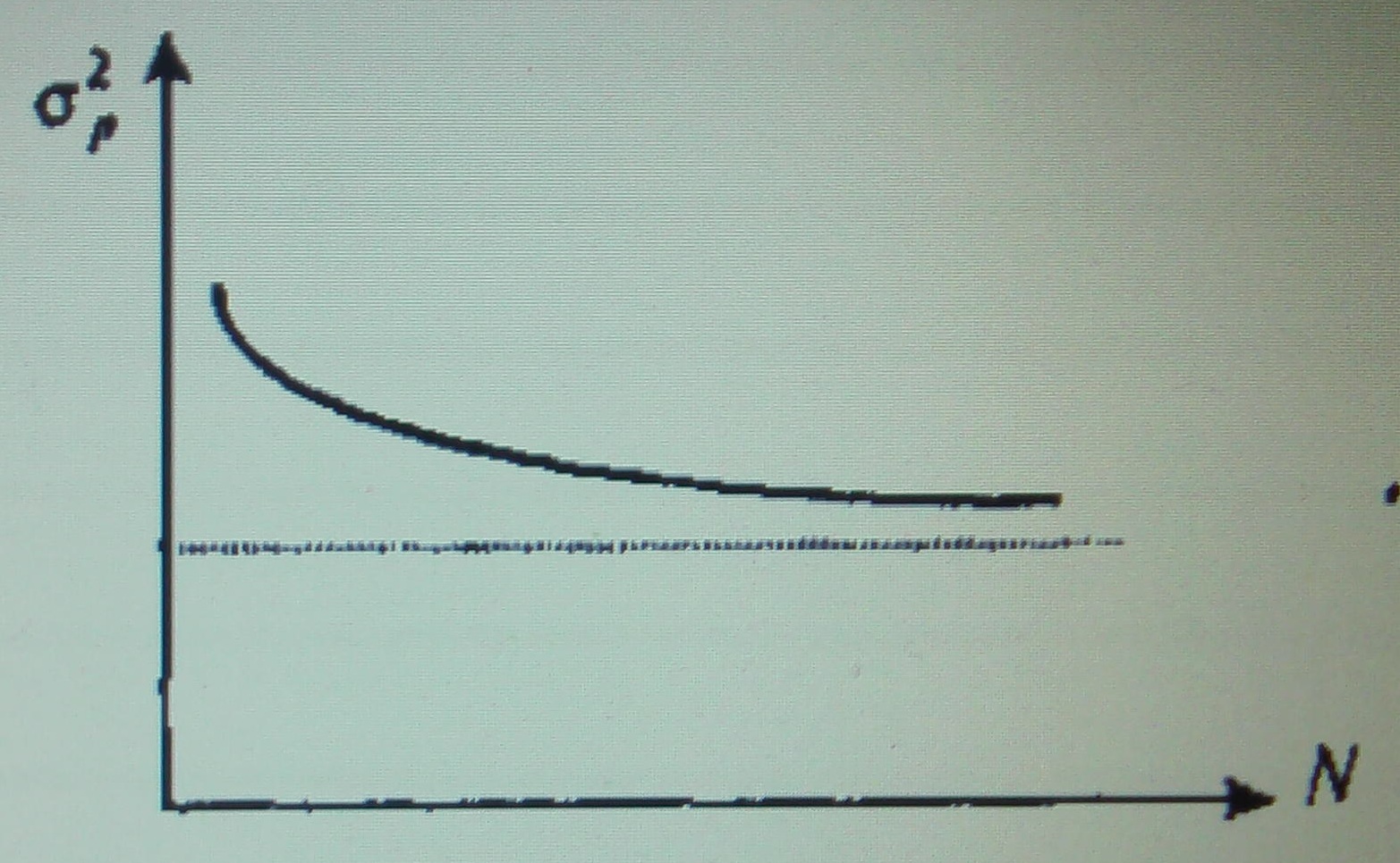
Этот прием позволяет свести риск портфеля к систематической составляющей.

Доказано эмпирически, что при N > 20 уникальный риск портфеля почти полностью исчезает. Конечно, если инвестор выбирает такие пары бумаг, что Pij ~ 1, то может оказаться достаточно большой. Поэтому, даже диверсифицированный портфель может быть «хорошо» или «плохо» диверсифицированным. Составление портфеля из акций фирмы, представляющих технологическую цепочку и, таким образом, сильно зависящих друг от друга, является хорошим примером «плохой» диверсификации.

11.1.5. Выбор портфеля. Теория рынка капитала

Каким же образом инвестор выбирает свой портфель?

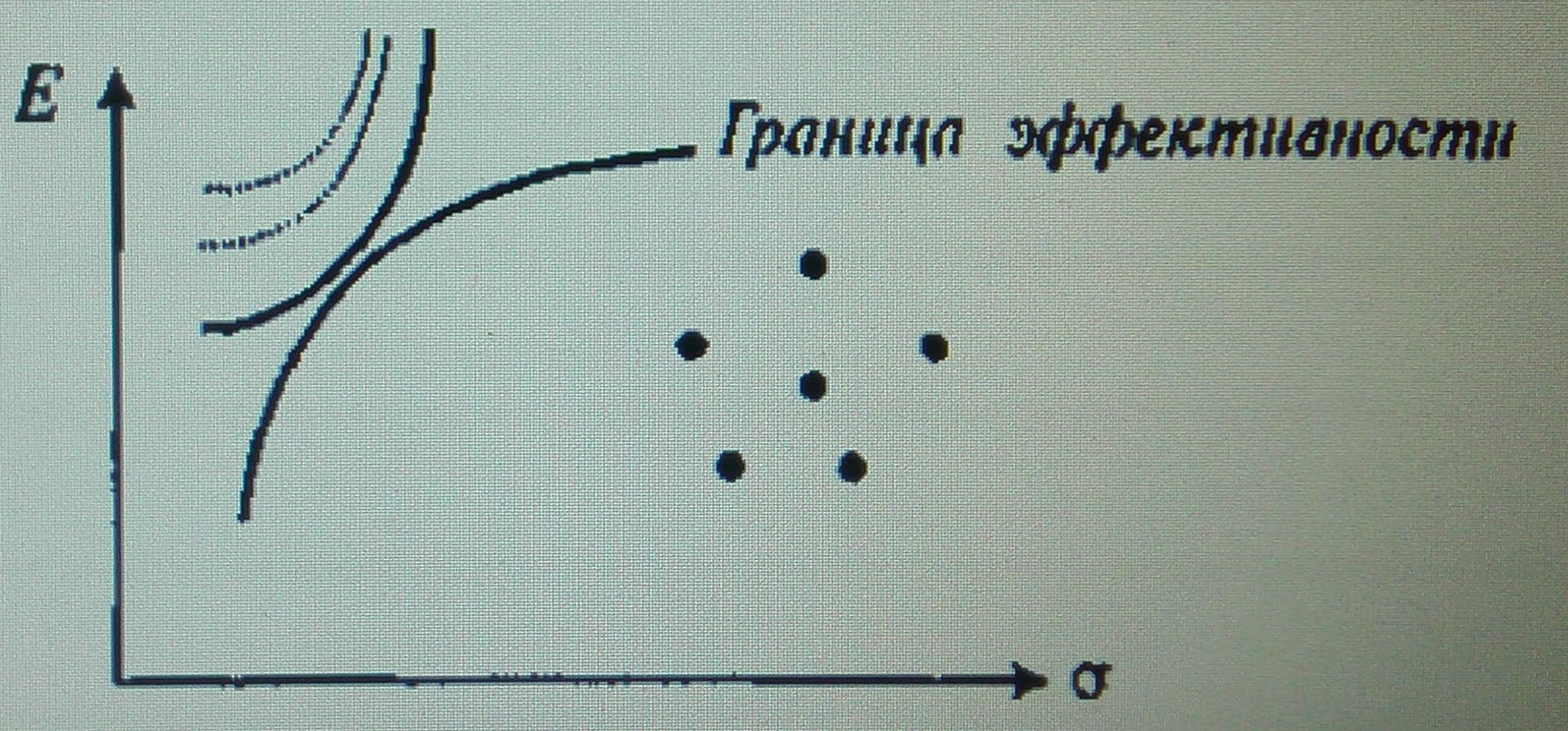
Естественно желание попасть на границу эффективности и получить при заданном риске максимальную доходность. Риск же зависит от предпочтений инвестора.

Точка касания границы эффективности и одной из кривых безразличия инвестора и есть тот самый «его» портфель. Кривые безразличия в подавляющем большинстве случаев являются параболой.

На рынке ценных бумаг обычно, кроме рискованных акций и облигаций, существуют безрисковые ценные бумаги, выпускаемые государством. Обозначим доход по этим бумагам rf . Если таких бумаг нет, инвестор может положить деньги в банк и иметь гарантированный минимальный доход. Риск такого вложения принимается равным нулю. Допустим, что и сам инвестор будет брать деньги в долг под такой же гарантированный процент.

Рассмотрим рисунок.

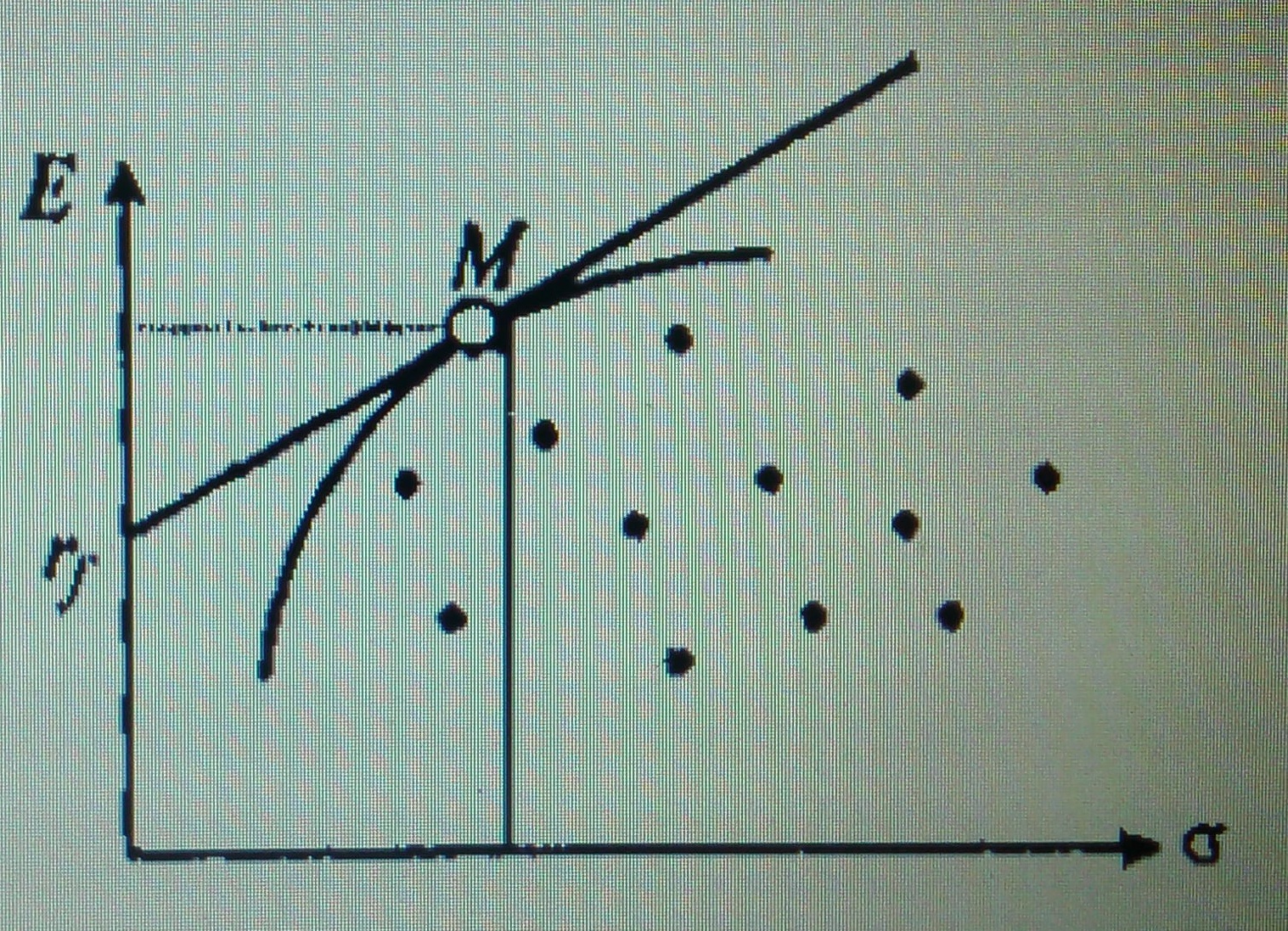
Прямая, проходящая через точку rf и касающаяся границы эффективности, называется прямой рынка капитала. Портфель в точке М называется рыночным портфелем. Покупая на часть своих средств безрисковые бумаги и вкладывая оставшуюся часть в рыночный портфель, инвестор оказывается на точке отрезка rfM, выше границы эффективности. Занимая средства под безрисковую ставку и вкладывая их вместе со своими в рыночный портфель, он находится на части прямойрыночного капитала правее точки М и снова выше границы эффективности. В какой именно точке прямой окажется инвестор, зависит от его рисковых предпочтений.

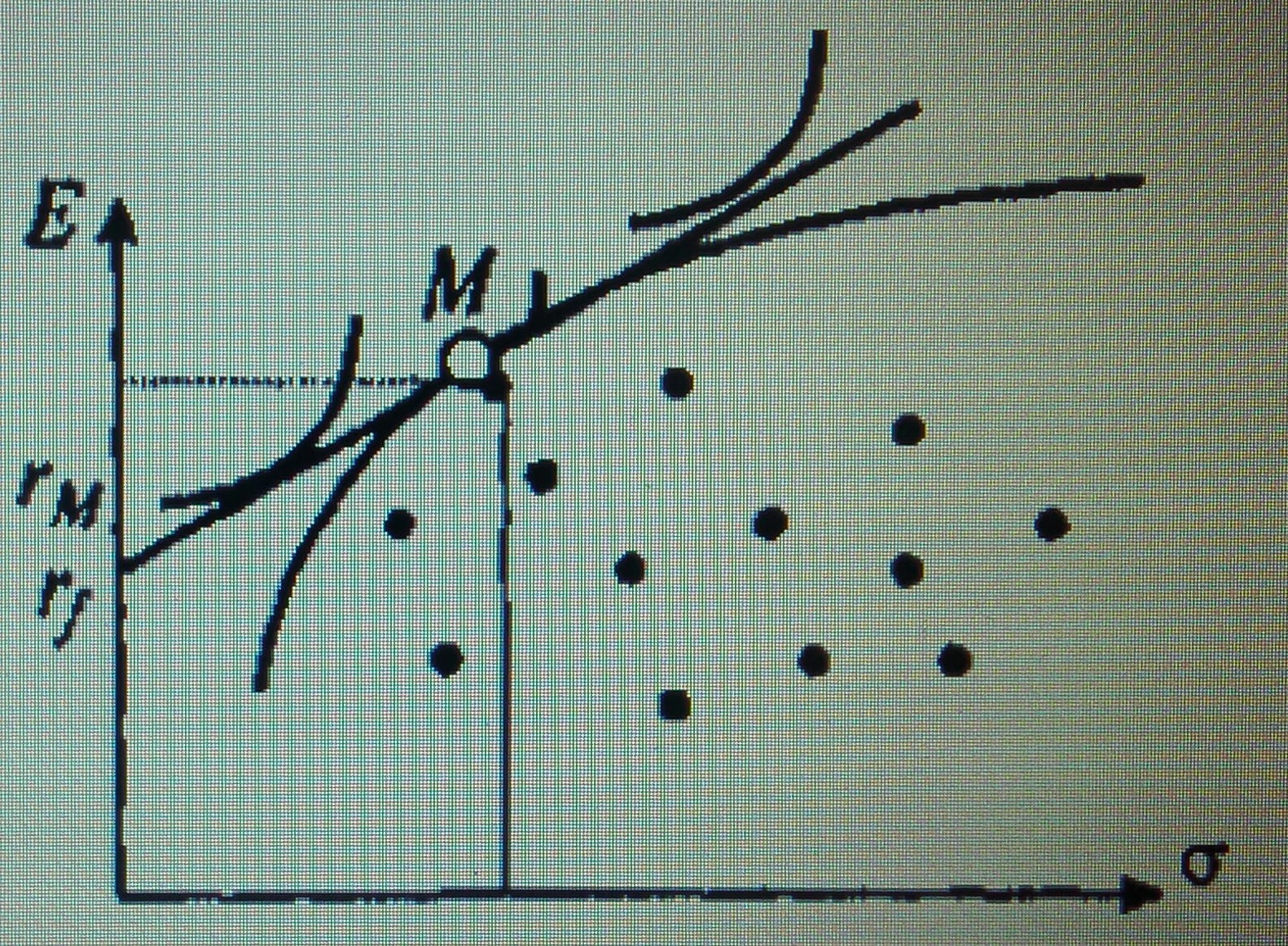
Теоретически можно, занимая деньги под безрисковую стайку и вкладывая их в рыночный портфель, достичь бесконечной доходности. Только риск при этом тоже бесконечен. Таким образом, при наличии безрисковой ставки на рынке ценных бумаг возникает один выделенный портфель, называемый рыночным. Тогда же появляется еще один способ описания качеств рискованных ценных бумаг. Их сравнивают с параметрами рыночного портфеля. Вместо Ei и σi вводят величину βi. Вообще, в отличие от вариации, коэффициент β аддитивен, что делает его очень удобным для оценки риска портфеля и целом.