Вопрос 7.
Определить понятие обратной матрицы и рассказать о способах ее вычисления.
Матрица B называется обратной к матрице A, если их произведение равно единичной матрице E. (B=A-1) (A-квадратная матрица)
Матрица A называется невырожденной, если ее определитель неравен 0 (rang A полный и нет зависимых строк (столбцов))
Если A - невырожденная, то тогда для матрицы существует обратная и находится по формуле:
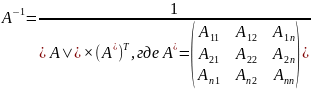
Матрицу A называют обратимой, если для нее существует обратная, в противном случае — необратимой. Для матрицы существует обратная при условии: исходная матрицы - квадратная, невырожденная (|A|≠0).
Свойства обратной матрицы:
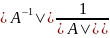
(AB)-1=A-1B-1
(AT)-1=(A-1)T
(kA)-1=k-1A-1, где k-любой коэффициент, неравный 0.
Вопрос 8.
Рассказать о крамеровских системах линейных уравнений и способе их решения.
Система линейных уравнений называется крамеровской, если число неизвестных совпадает с числом уравнений и определитель основной матрицы системы линейных уравнений не равен 0. Тогда система линейных уравнений имеет решение, причем только одно.
Решением
крамеровской системы линейных уравнений
является выражение следующего вида:
,
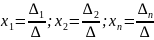где ∆=|A|, ∆i
- определитель матрицы, получаемый из
основной, с помощью замены i-ого
столбца на столбец свободных членов.
Вопрос 9.
Раскрыть суть метода Гаусса для решений линейных уравнений общего вида.
Метод Гаусса — классический метод решения системы линейных уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида (трапециевидного вида), из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
На первом этапе необходимо записать расширенную матрицу (основная матрица плюс столбец свободных членов).
Путем элементарных преобразований приводим матрицу к трапециевидному виду.
Выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Количество базисных переменных равно рангу матрицы, составленной из коэффициентов системы.
Вопрос 10.
Критерий совместности систем линейных уравнений (теорема Кронекера - Капелли).
Формулировка:
Система линейных уравнений совместна тогда и только тогда, когда ранг основной матрицы равен рангу расширенной. Если ранги матриц равны числу неизвестных, то с.л.у. имеет единственное решение, если же ранги меньше числа неизвестных, то система имеет более одного решения.