Глава 2. Проверка статистических гипотез.

§1. Основные понятия.

Статистическая гипотеза – это некоторое предположение относительно генеральной совокупности, проверяемое по выборочным данным.

Примеры статистических гипотез:

1. Нормально распределённая случайная величина X имеет генеральную среднюю a, равную a₀ – H₀: a=a₀.

2. Нормально распределённая случайная величина X имеет дисперсию σ², равную σ² – Н₀: σ²= .

3. Выборка x=(x₁, x₂, …, x_n) извлечена из нормально распределённой генеральной совокупности.

Различают гипотезы параметрические и непараметрические.

Гипотеза называется параметрической, если в ней содержится утверждение о параметре распределения известного вида.

Гипотеза называется непараметрической, если она выдвигает утверждение о виде неизвестного закона распределения случайной величины.

Гипотеза, которую следует проверить, называется основной или нулевой гипотезой H₀. Вместе с нулевой гипотезой рассматривают конкурирующую или альтернативную гипотезу H₁. Эта гипотеза является отрицанием нулевой гипотезы.

Параметрическая гипотеза называется простой, если она содержит предположение равно об одном значении параметра.

H₀: λ=5 – параметр показательного распределения λ

H₀: X – нормально распределённая случайная величина

a=a₀, σ известна

Параметрическая гипотеза называется сложной, если она состоит из конечного или бесконечного множества простых гипотез.

H₀: X – нормально распределённая случайная величина

a=a₀, σ неизвестна

Статистику, значение которой находят по выборке, и по этому значению выносят решение: принять или не принять основную гипотезу, называют статистическим критерием. При этом используют правило, которое устанавливает, при каких числовых значениях статистики нулевая гипотеза принимается, а при каких – нет.

Схема проверки гипотезы.

Всё множество возможных значений статистики делится на два непересекающихся подмножества:

Область S – область отклонения основной гипотезы

Область - область принятия основной гипотезы

Область S называется критической. Если вычисленное по выборке значение статистики попадает в область S, то нулевая гипотеза H₀ отклоняется. Если вычисленное по выборке значение статистики попадает в область , то нулевая гипотеза H₀ принимается.

В итоге статистической проверки гипотезы могут иметь место ошибки двух родов:

1. Ошибка 1-го рода – будет отвергнута правильная гипотеза H₀. Вероятность ошибки 1-го рода – α, , где α – уровень значимости. Обычно в качестве α берётся 0,1; 0,05; 0,01; 0,005.

2. Ошибка 2-го рода состоит в том, что будет принята неправильная гипотеза H₀. Вероятность этого события – β, , . Число (1-β) – мощность критерия. Геометрически мощности критерия – вероятность попадания в критическую область, когда гипотеза неверна.

Пример.

Завод выпускает лампочки нового типа и предполагаем, что средний срок службы таких ламп будет не менее 1500 часов. Для выборки из 80 ламп оказалось, что средний срок службы ламп равен 1475 часов. Среднее квадратическое отклонение σ известно и σ=100 часов. Проверить гипотезу, выдвинутую фирмой при уровне значимости α=0,1 и построить график функции 1-β=(1-β)(a). Считать, что X – срок службы – нормально распределённая случайная величина.

Решение.

H_o: a₀=1500

H₁: a₀=a₁<1500

(Случай a>1500 нас не интересует, т.к. какие-либо действия следует принимать, если срок службы лампочек <1500 ч).

При такой гипотезе H₁ критическая область является левосторонней.

В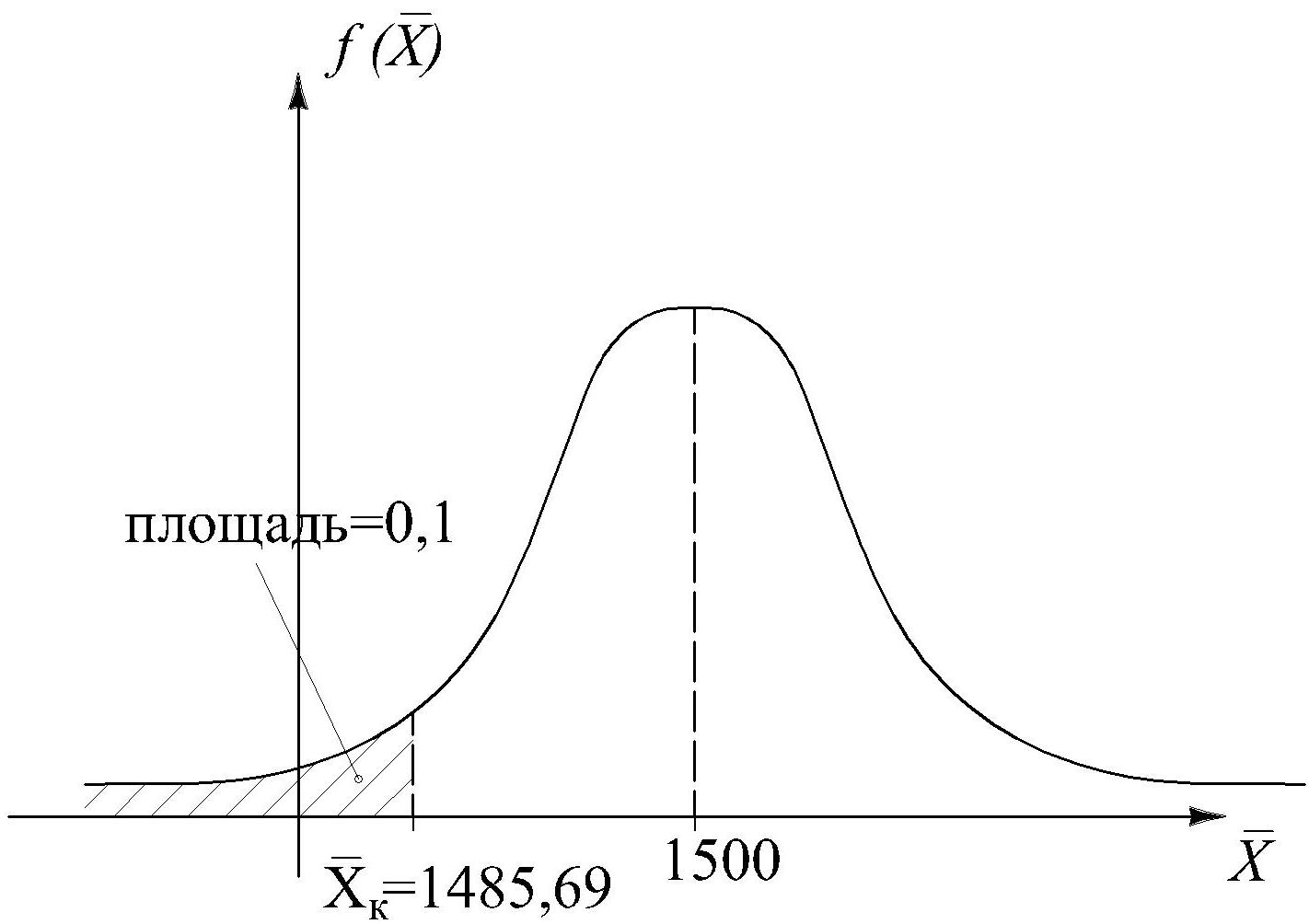 ероятность ошибки I-го рода – площадь по графиком нормального распределения выборочной средней слева от левосторонней критической границы. Найдём эту границу ; . По таблице нормального распределения U_2α=1,28. .

Найденное по выборке значение статистики , нулевая гипотеза H₀ отвергается. Говорят: средний срок службы лампочек значимо меньше 1500 часов.

Построим график функции 1-β=(1-β)(a).

П редположим, что нулевая гипотеза неверна и a=1490. (1-β) – вероятность попасть в критическую область S, т.е. получить . Следовательно, (1-β) – площадь под графиком распределения выборочной средней при a=1490 левее 1485,69. Эта площадь –

Возьмём другое значение a=1480.

(площадь под графиком левее 1485,69).

Е сли a=1430, то =0,5+Φ(4,98)=0,5+0,499=0,999.

График функции 1-β=(1-β)(a) имеет вид (a=1500, 1-β=α=0,1):

Мы построили график функции мощности в случае левосторонней критической границы.

Е сли критическая граница будет правосторонней, то график функции будет симметричным графику для левосторонней критической границы относительно вертикали a₀.

В случае двусторонних критических границ график выглядит следующим образом:

Свойства мощности критерия (1-β).

Мощность зависит от расстояния между a₀ и действительным значением a, среднего квадратического отклонения генеральной совокупности, размера выборки и уровня значимости.

1. Чем больше расстояние между a₀ и действительным значением a, тем больше вероятность заметить неверность нулевой гипотезы.

2. Чем меньше σ – среднее квадратичекое отклонение генеральной совокупности, тем больше мощность критерия.

3. Чем больше размер выборки, тем больше мощность критерия.

4. Чем меньше уровень значимости, тем меньше мощность критерия.