§12. Интервальные оценки параметров нормального распределения.

Вычисленная на основе выборки точечная оценка θ* является лишь приближением к неизвестному значению параметра θ даже в том случае, когда оценка является состоятельной, несмещённой и эффективной.

Пусть γ=1-α – заданная, близкая к единице вероятность.

Если , (1)

то интервал (θ*-δ,θ*+δ) называется интервальной оценкой параметра θ или доверительным интервалом.

γ=0,99; γ=0,95; … γ=0,9 и т.д.

Точечная оценка θ* - случайная величина; число δ – ошибка оценки, случайная величина, которая зависит выборки и от γ (надёжность оценки или доверительная вероятность). Поэтому доверительный интервал также случайный.

Выражение (1) понимают так: интервал (θ*-δ,θ*+δ) накроет истинное значение параметра θ с вероятностью γ.

Схема построения интервальной оценки при конечном объёме выборки n.

1. Подбирается функция ψ(θ*,θ), которая удовлетворяет следующим двум условиям:

   1. закон распределения ψ(θ*,θ) известен, но не зависит от θ

   2. функция ψ непрерывна и строго монотонна по параметру θ

2. Задав доверительный интервал γ=1-α, находят двусторонние критические границы и , отвечающие вероятности γ=1-α. Тогда с вероятностью γ выполняется неравенство (2) Решив это неравенство (2) относительно θ, находят границы доверительного интервала: θ*-δ – нижняя граница доверительного интервала, θ*+δ – верхняя граница доверительного интервала Функцию ψ(θ*,θ) называют статистикой. Если плотность распределения ψ(θ*,θ) симметрична относительно оси OY, то доверительный интервал симметричен относительно θ*.

Общая схема построения доверительного интервала.

1. Из генеральной совокупности с известным распределением f(x,θ) случайной величины X извлекается выборка объёма n, и по ней находится точечная оценка θ* параметра θ.

2. Выбирается статистика ψ(θ*,θ), закон распределения которой известен.

3. Задаётся уровень значимости α (вероятность; 1-α=γ – надёжность оценки).

4. Находят двусторонние критические границы распределения ψ(θ*,θ), тогда , и при этом .

В задачах экономики часто приходится находить интервальные оценки параметров распределения для случайных величин, имеющих нормальное распределение, поэтому будем строить оценки параметров нормально распределённой случайной величины.

Доверительные интервалы для оценки математического ожидания.

1. σ – среднее квадратическое отклонение генеральной совокупности – известно. Для получения доверительного интервала наименьшей длины при заданном объёме выборки n, при заданной доверительной вероятности в качестве точечной оценки параметра следует брать эффективную оценку. Для нормально распределённой случайной величины X эффективной оценкой является выборочная средняя (случайная величина).

Теорема.

Если генеральная случайная величина X имеет нормальное распределение с математическим ожиданием a и средним квадратическим отклонением σ, то случайная величина имеет также нормальное распределение с тем же математическим ожиданием и , где n – объём выборки.

Доказательство.

Было доказано, что . Теперь найдём дисперсию ; .

Случайная величина называется центрированной, если её математическое ожидание равняется нулю. Для того, чтобы центрировать случайную величину, из неё нужно вычесть математическое ожидание. Действительно, .

Случайная величина называется нормированной, если её дисперсия равняется единице. Чтобы нормировать случайную величину, нужно её поделить на среднее квадратическое отклонение σ: .

Центрированная и нормированная случайная величина называется стандартной. Стандартное нормальное распределение: a=0, σ=1.

Интервальная оценка для математического ожидания, когда σ известно.

Случайная величина имеет стандартное нормальное распределение. M(z)=0, σ=1.

1. распределение z не зависит от a

2. как функция параметра a, она непрерывна и строго монотонна

z может быть взята в качестве статистики. При помощи этой статистики проведём построение доверительного интервала.

Для стандартной нормально распределённой случайной величины двусторонние критические границы (-U_α,U_α):

α – задана, .

Решим это неравенство относительно a:

; - ошибка оценки.

Для нормально распределённой случайной величины в курсе теории вероятностей мы установили: ; .

Значение U_α находится по таблицам функции Лапласа из условия, что .

Пример.

Найти доверительный интервал с надёжностью 0,8 для оценки математического ожидания нормально распределённой случайной величины со средним квадратическим отклонением σ=5, выборочной средней и объёмом выборки n=25.

1) , и ; 2) ; ;

3) γ=0,8; ; U_α=1,28; 4) 20-1,28<a<20+1,28.

Ответ: .

2. σ – неизвестно. X – нормально распределённая случайная величина. В этом случае вместо σ² будем использовать исправленную выборочную дисперсию S², которую рассчитываем на основе имеющейся выборки. Построение интервальной оценки для математического ожидания a основано на статистике: . При случайной выборке из нормальной генеральной совокупности эта статистика имеет распределение Стьюдента с (n-1) степенью свободы независимо от значения параметра a. ; ; . Число t_α находят по таблице распределения Стьюдента с числом степеней свободы k=n-1 и с вероятностью P=α.

Замечание 1: если (n-1)>30 (большой объём выборки), то случайная величина t(n-1) имеет распределение, близкое к стандартному нормальному распределению. В этом случае: , где .

Замечание 2: в случае одной и той же генеральной совокупности

1. для фиксированного объёма выборки n, чем выше уровень надёжности γ=1-α, тем шире доверительный интервал

2. при фиксированном значении надёжности оценки, чем больше объём выборки n, тем уже доверительный интервал

Пример.

Из генеральной совокупности извлечена выборка объёмом n=16 и найдена выборочная средняя , получено значение несмещённой выборочной дисперсии S²=9, γ=0,9. X имеет нормальное распределение. Найти оценку для математического ожидания.

1) , и , т.к. (n-1)=15<30; 2)α=0,1; ; 3) ; 4) 30-1,3125<a<30+1,3125.

Ответ: .

Доверительный интервал для оценки среднего квадратического отклонения σ при неизвестном математическом ожидании.

X имеет нормальное распределение, необходимо найти оценку для среднего квадратического отклонения. Наилучшей точечной оценкой дисперсии в этом случае является исправленная выборочная дисперсия . Построение интервальной оценки для σ² основано на статистике . При случайной выборке из генеральной совокупности эта случайная величина имеет распределение χ² с (n-1) степенью свободы.

, где и - двусторонние критические границы распределения χ² с (n-1) степенью свободы.

Решив это неравенство относительно σ², получим, что с вероятностью γ=1-α выполняется неравенство , и с такой же вероятностью выполняется неравенство .

Двусторонние границы и находят по таблице, где приведены критические точки распределения χ² при числе степеней свободы (n-1) и с вероятностью и .

Пример.

По некоторой отрасли составлена случайная выборка из 19 фирм. По выборке оказалось, что несмещённое значение выборочного среднего квадратического отклонения S=25. Пользуясь 90%-м доверительным интервалом, оценить вариацию работающих в фирме по всей отрасли.

Решение.

По условию n=19, S=25, 1-α=0,9. k=n-1=18. По таблице при p=0,05 найдём верхнюю доверительную границу ; при нижнюю доверительную границу . Тогда , или .

Ответ: .

Доверительный интервал для вероятности.

Пусть проводится испытание Бернулли, вероятность успеха p неизвестна. Требуется построить интервальную оценку вероятности успеха в единичном испытании. Точечной оценкой вероятности является относительная частота, определяемая по выборке. При (большие выборки) - распределение p* является нормальным.

Построение доверительного интервала основано на статистике - стандартная нормально распределённая случайная величина.

Решаем это неравенство относительно p

Пример.

Проводя маркетинговые исследования, фирма решила оценить долю фирм на российском рынке определённых продуктов. Было случайно выбрано 100 потребителей, и оказалось, что 26 используют иностранную продукцию, остальные – произведённую в РФ. Построить 95%-й доверительный интервал для доли иностранного продукта на рынке.

γ=0,95 n=100

α=1-0,95=0,05 p*=0,26

; U_α=Φ(0,475)=1,96

; ; .

Ответ: .

Объём выборки.

Объём выборки определяет стоимость проведения исследования. От объёма выборки зависит надёжность оценки и размер доверительного интервала. Минимальный объём выборки определяется двумя параметрами:

1. Ошибкой оценки δ.

2. Надёжностью оценки γ.

Пусть задана , затем из формулы (ошибка оценки) находим .

1. Если σ известно, то сразу находим n.

2. Если σ неизвестно:

1. известны x_max и x_min – самое большое и самое маленькое значения генеральной совокупности (размах)

З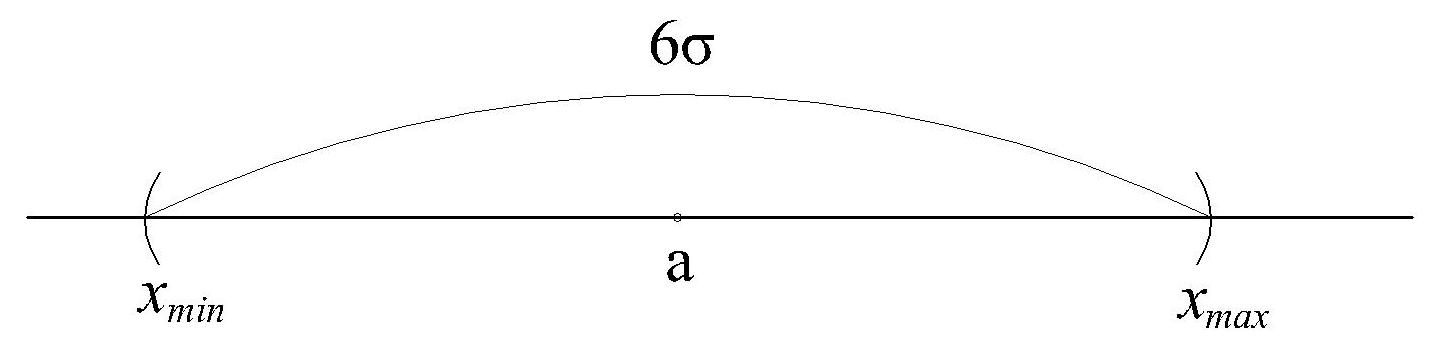 ная размах, находим σ, и затем объём выборки n:

6σ= x_max-x_min

2. нет информации, тогда берём S (находим по выборке) в качестве σ

3. если есть p* (относительная частота); , если мы знаем хотя бы приближённое значение для успеха p. Если никакой оценки вероятности успеха p нет, то мы её оцениваем. , тогда

Отсюда получаем оценку .

Пример 1.

Фирма коммунального хозяйства желает на основе выборки оценить среднюю квартплату за квартиры определённого типа с надёжностью не менее 99% и погрешностью менее 10 денежных единиц. Предполагается, что квартплата имеет нормальное распределение со средним квадратическим отклонением, не превышающим 35 денежных единиц. Найти минимальный объём выборки.

Решение.

Требуется найти такое n, при котором . По таблице функции Лапласа найдём U_α такое, что ; . При δ=10 и σ=35 получим из формулы ; ; n=82,81. Т.к. с ростом γ=1-α и уменьшением ошибки оценки δ растёт n, то n≥82,81 и n_min=83.

Ответ: n_min=83.

Пример 2.

Компания оценивает свою долю рынка как 20%. Найти минимальный объём выборки, требуемой для оценки действительной доли с точностью до 5% и надёжностью 90%.

Решение.

1) ; ;

2) ; 3) ; n=173,1856; n_min=174.

Ответ: n_min=174.