§10. Критические границы.

Это понятие для непрерывных случайных величин широко используется в математической статистике при построении доверительных интервалов и критериев проверки гипотез. Различают левосторонние, правосторонние и двусторонние критические границы.

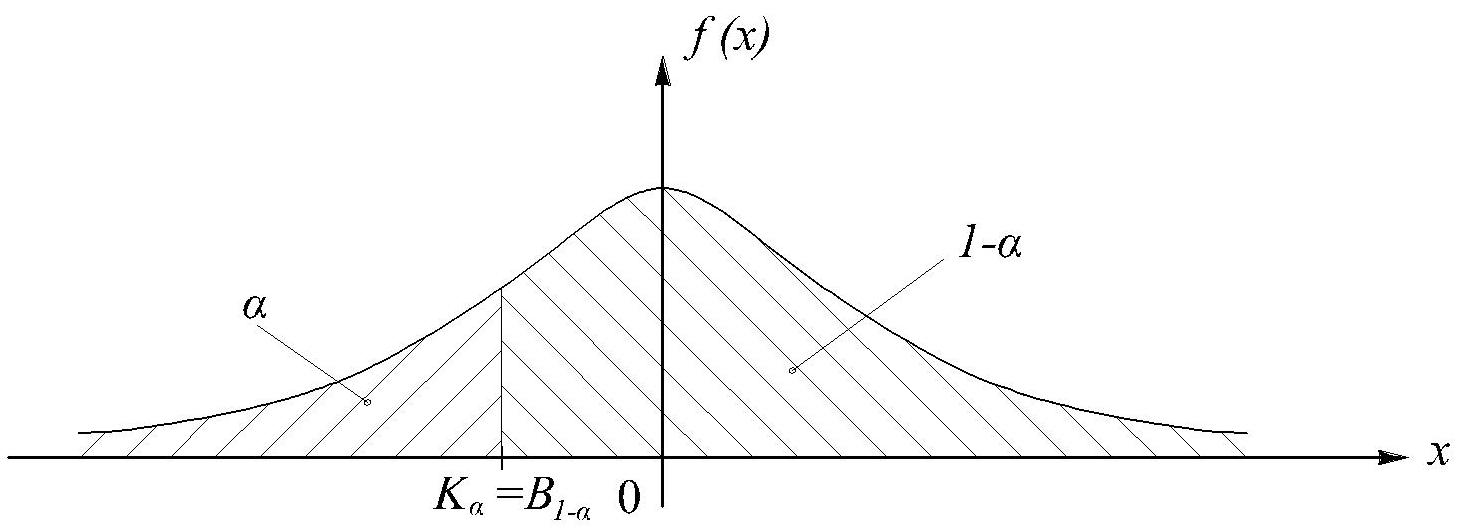
Левосторонней критической границей, или квантилью, отвечающей вероятности α, называется такая граница K_α, левее которой вероятность равна α.

, т.о. квантиль определяется критерием: (1).

П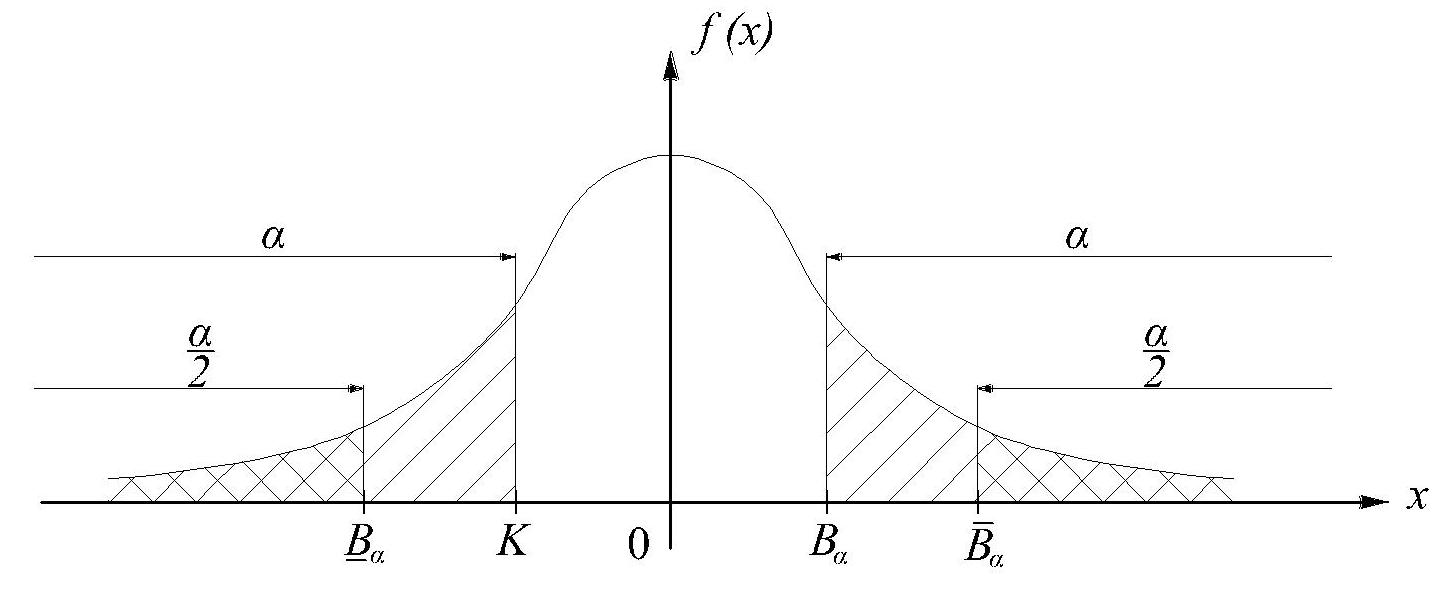 равосторонней критической границей, отвечающей вероятности α, называется такая граница B_α, правее которой вероятность равна α.

По определению: . Правосторонняя граница является решением уравнения (2).

Установим связь между правосторонней и левосторонней границами:

Двусторонними критическими границами, отвечающими вероятности α, называются такие границы и , внутрь которых случайная величина попадает с вероятностью (1-α), а вне интервала, определяемого этими границами - с вероятностью α, причём .

Таким образом, двусторонние критические границы являются решением уравнений:

; .

Между односторонними и двусторонними границами существующие соотношения определяются равенствами:

; .

Для стандартного нормального распределения двусторонние критические границы симметричны и обозначаются , т.е. , .

В дальнейшем мы убедимся в том, что .

§11. Основные законы распределения статистических оценок.

В качестве законов распределения статистических оценок используют следующие распределения.

Распределение χ².

Пусть X₀, X₁, …, X_n – независимые, стандартные, нормальные случайные величины (a=0, σ=1).

Распределение суммы квадратов этих случайных величин называется распределением χ² с n степенями свободы:

.

Число степеней свободы равно разности общего числа неизвестных и связей между этими неизвестными.

И зобразим графики функции плотности для разных степеней свободы:

Значение χ² распределения находится по таблице. При построении доверительных интервалов и проверке гипотез используются двусторонние критические границы χ². Поскольку двусторонние критические границы можно определить по односторонним, то обычно в таблице приводятся только правосторонние критические границы для каждого значения степеней свободы.

Распределение Стьюдента.

Рассмотрим случайную величину 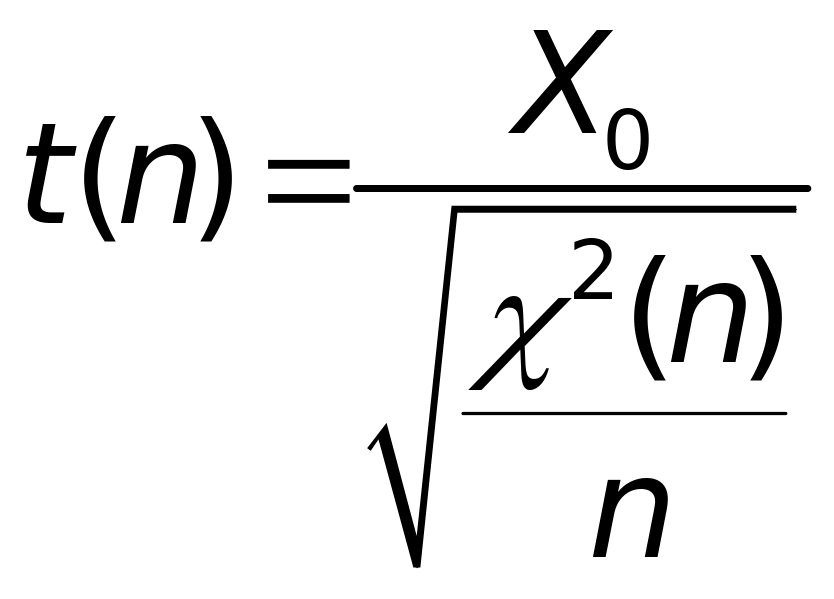, где X₀ – стандартное нормальное распределение, причём случайная величина X₀ и - независимые. Такое распределение называется распределением Стьюдента с n степенями свободы. При распределение Стьюдента стремится к нормальному.

Г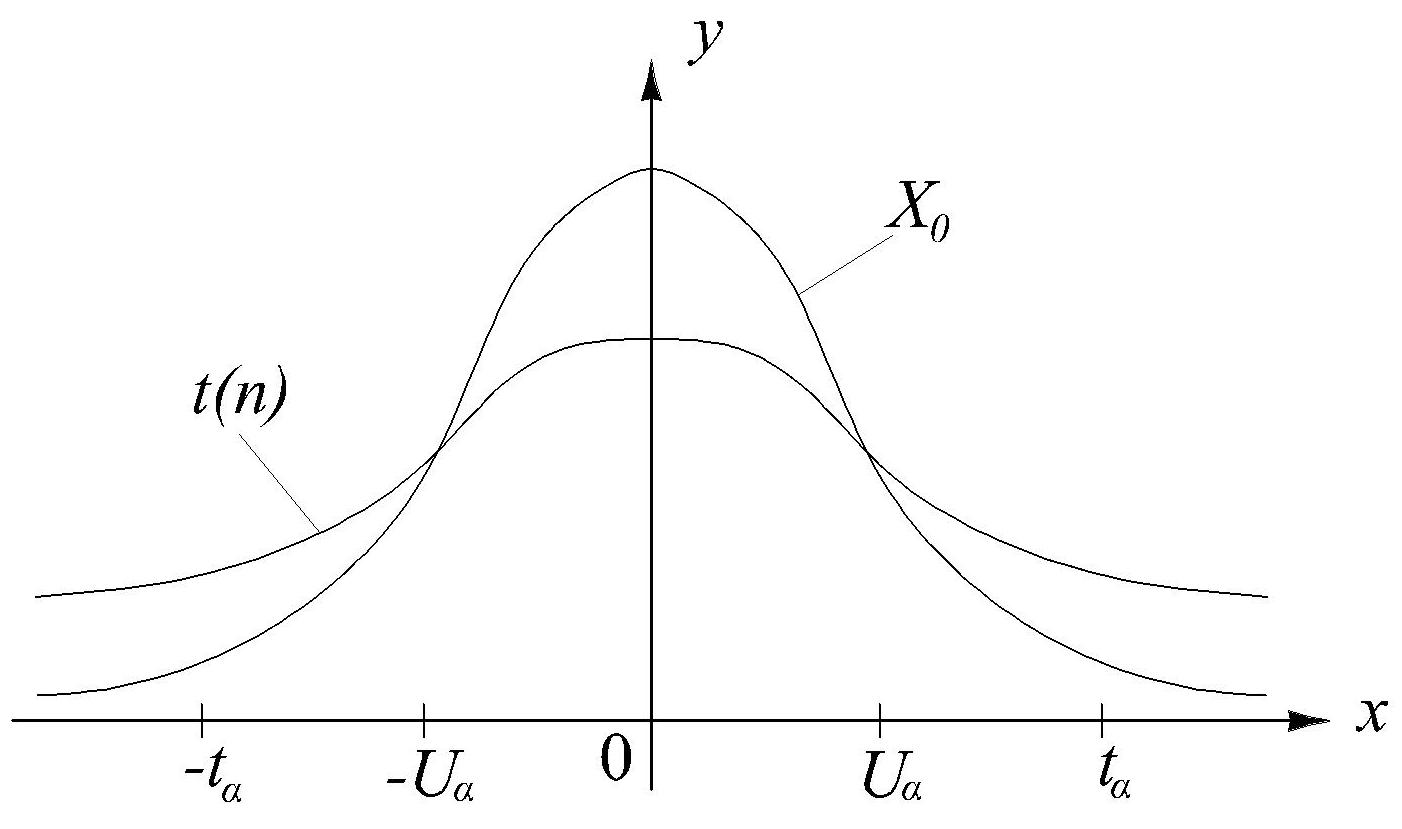 рафик плотности распределения Стьюдента является симметричным, но более плоским, чем график плотности нормального распределения и выше графика нормального распределения по краям. Двусторонние критические границы распределения Стьюдента шире соответствующих двусторонних границ нормального распределения: t_α>U_α. Обычно в таблице приводятся правосторонние двусторонние границы t_α(n) для разных значений степеней свободы.

Распределение Фишера.

χ²(m), χ²(n) – независимые случайные величины, имеющие распределение χ² с m и n степенями свободы соответственно.

- распределение Фишера с m и n степенями свободы.