§6. Полигон и гистограмма.

Статистическое распределение выборки графически отображается в виде полиго-на и гистограммы.

Дискретный ряд распределения отображается в виде полигона.

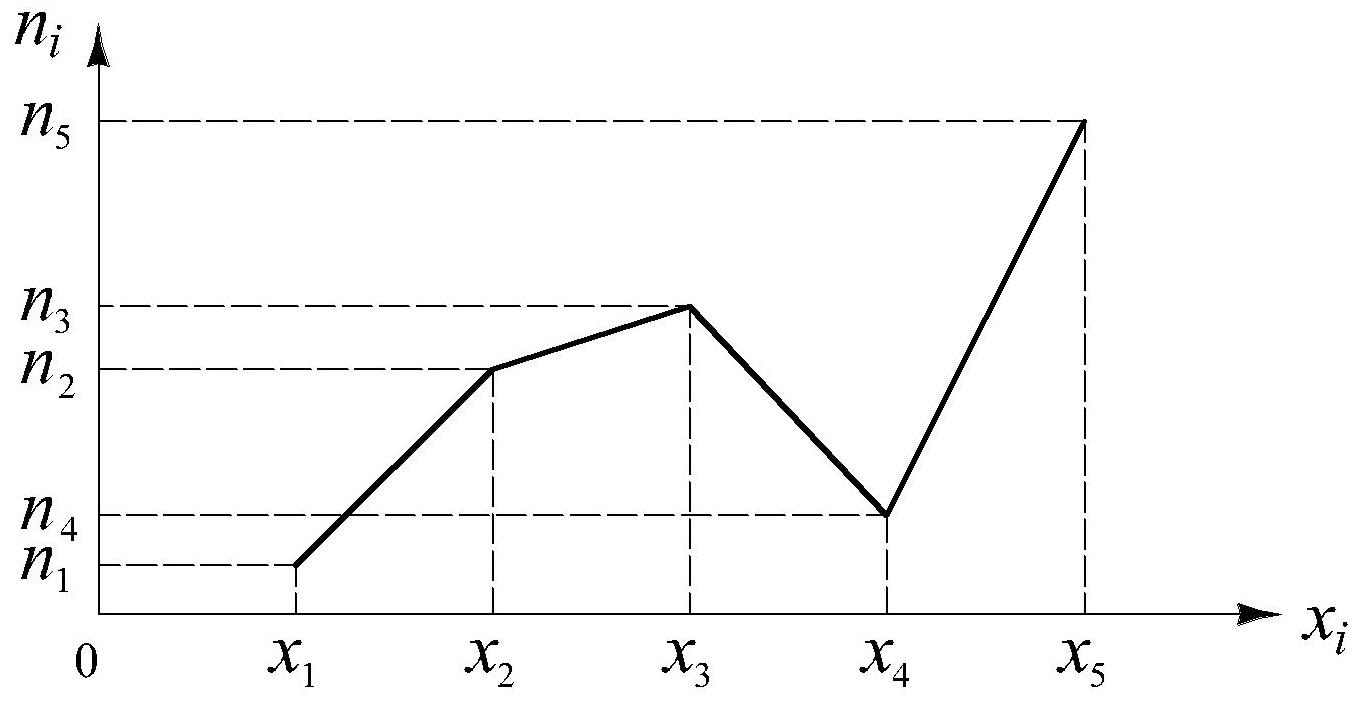
(x_i, n_i) – полигон частот

Можно построить полигон относитель-ных частот.

Интервальный ряд распределе-ния отображается графически при по-мощи гисто­граммы. По оси абсцисс откладываются интервалы, и на каждом из них строится прямоуголь­ник, площадь которого равна относительной частоте данного интервала, а высота прямоугольника равна относительной частоте интервала, поделённой на его длину, т.е. .

, площадь под гистограммой - .

Величину называют плотностью относительной частоты, она является оцен-кой плотности вероятности f(x) генеральной совокупности.

Пример.

Выборка задана интервальным рядом распределения. Построить гистограмму выбо­рочной оценки плотности вероятности.

Ii	(-4,-3)	(-3,-2)	(-2,-1)	(-1,0)	(0,1)	(1,2)	(2,3)	(3,4)
mi	6	25	72	133	120	88	46	10
		0,05	0,144	0,266	0,24	0,176	0,092	0,02

; n=500

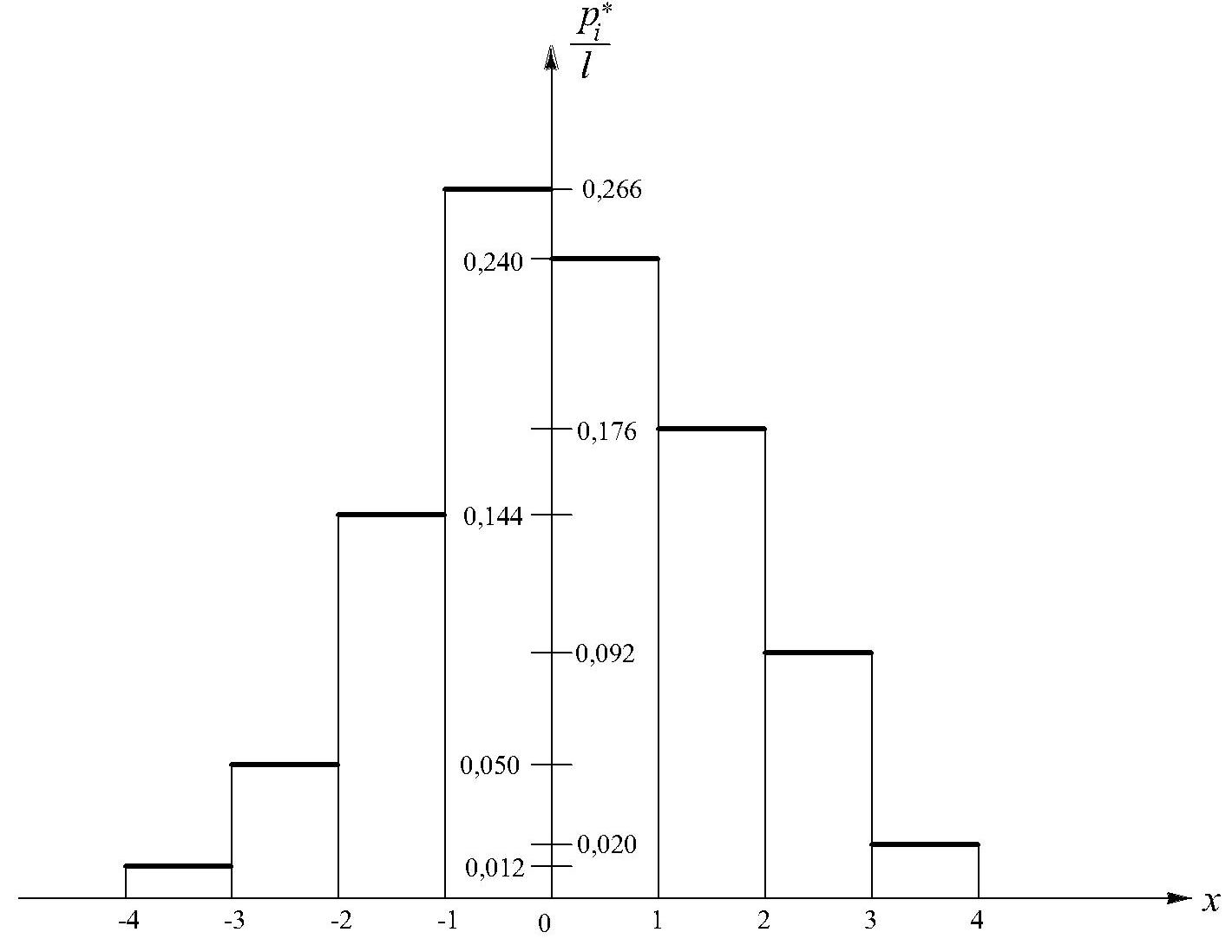
Высота столбика точно отображает количество значений выборочных данных, которые принадлежат соответствующему интервалу, и даёт наглядное представление о местах с повышенной концентрацией данных. Используя эти данные, при помощи интервального ряда распределения можно приближённо построить эмпирическую функцию распределения.

F*(-4) =0; F*(-3) =0,012;

F*(-2) =0,062; F*(-1) =0,206;

F*(0) =0,472;

F*(1) =0,712; F*(2) =0,888;

F*(3) =0,980; F*(4) =1.

§7. Статистические оценки.

Рассмотрим задачу оценки закона распределения генеральной случайной величины на основе выборочных данных. Пусть вид закона распределения генеральной случайной величины известен, но неизвестны его параметры, например, математическое ожидание и дисперсия.

Требуется на основе выборочных данных найти приближённые значения этих параметров, т.е. найти статистические оценки этих параметров.

Существует два подхода к оценке неизвестных параметров распределения по наблюдениям:

1. точечный – указывает лишь точку, около которой находится оцениваемый параметр

2. интервальный – находят интервал, который с заданной вероятностью накрывает числовое значение параметра

θ* - оценка неизвестного параметра θ.

Пусть в результате n независимых наблюдений над генеральной случайной величиной получена конкретная выборка x₁, x₂, …, x_n. По этой выборке мы можем рассчитать оценку θ*.

Если бы мы имели k конкретных выборок того же объёма n, то для каждой такой выборки мы смогли бы рассчитать оценки параметра θ: - различные числа, т.е. мы бы получили разные оценки.

Таким образом, оценку θ* можно рассматривать как случайную величину, а - это её конкретные реализации.

Понимая под случайной выборкой весь мыслимый набор конкретных выборок, определим оценку θ* как функцию от случайной выборки, где X₁, X₂, …, X_k - независимые, одинаково распределённые случайные величины, и распределение – такое же, как распределение генеральной случайной величины (т.к. все они имеют одно и то же математическое ожидание a и дисперсию σ²): .

Как определить качество оценки? Качество определяют, проверяя, выполняются ли следующие три свойства:

1. состоятельность оценки – оценка θ* называется состоятельной, если она сходится по вероятности к истинному значению оценки θ*, т.е.

Это свойство является обязательным, несостоятельные оценки не рассматриваются.

2. несмещённость оценки – оценка называется несмещённой, если M(θ*) равно её истинному значению θ

Это свойство является желательным, но не обязательным. Если полученная нами оценка является смещённой, то её можно поправить так, чтобы она стала несмещённой.

3. эффективность оценки – оценка называется эффективной, если она - самая точная в данном классе оценок θ*, т.е. имеет минимальную дисперсию

Выборочная средняя.

Выборочной средней называется среднее арифметическое значений выборки.

Если все варианты выборки различны, то: .

Если варианты имеют частоты: , - объём выборки.

В ряде случаев все выборочные значения разбиваются на отдельные группы, и в каждой группе находится её среднее значение; среднее значение для группы - групповая средняя . Зная групповые средние, находят общую среднюю для всей выборки и обозначают .

Пример.

Найти общую среднюю на основе выборки:

Группа	1		2
Значение варианты	1	6	1	5
Частота	10	15	20	30
Объём	25		50

Требуется найти групповые средние и общую среднюю.

;

.

Ответ: .

Выборочную среднюю используют в качестве оценки для математического ожидания.

Пусть x₁, x₂, …, x_n – конкретная выборка; X₁, X₂, …, X_n – случайная выборка (все эти случайные величины имеют одно и то же математическое ожидание a и дисперсию σ²).

Для случайной выборки: .

1. Согласно закону больших чисел - среднее арифметическое независимых, одинаково распределённых случайных величин, имеющих дисперсию σ², сходится по вероятности к их математическому ожиданию a. Это означает, что - оценка состоятельная.

2. Несмещённость оценки проверим непосредственно. , т.е. оценка является несмещённой.

3. Свойство эффективности. Если распределение генеральной случайной величины – нормальное, то можно доказать, что оценка является эффективной.

Выборочная дисперсия.

Выборочная дисперсия является характеристикой рассеивания выборочных значений относительно выборочной средней.

Выборочной дисперсией называется ( ) среднее арифметическое квадратов отклонений вариант от выборочной средней.

Если все варианты различны:

Если варианты сгруппированы по частотам:

- объём выборки

- выборочное среднее квадратическое отклонение (стандартная ошибка).

Для случайной выборки выборочная дисперсия имеет вид: .

Проверим эту оценку на несмещённость:

Рассмотрим каждое слагаемое суммы:

1)

2)

3)

Получим

Оценка имеет систематическое смещение . Это смещение сходит на «нет» при , т.е. оценка асимптотически не смещена.

Поправим так, чтобы она стала несмещённой: - исправленная выборочная дисперсия.

Можно показать, что оценка также является состоятельной.

Теорема.

Выборочная дисперсия равна разности среднего арифметического квадратов значений выборки и квадрата выборочной средней: .

Доказательство.

Пусть выборочные значения (варианты) имеют частоту, тогда

Пример.

Из генеральной совокупности извлечена выборка:

xi	-8	-2	1	5
ni	13	11	14	12
	-6,96	-0,96	2,04	6,04

n=50

Требуется найти выборочную и исправленную дисперсии.

; ;

Ответ: , .

Оценка вероятности.

Пусть в генеральной совокупности проводится испытание Бернулли и вероятность успеха p в одном испытании неизвестна.

Оценкой для параметра p является относительная частота , где X – суммарное число успехов за n испытаний, n – объём выборки, p* - конкретное значение относительной частоты.

Если n фиксировано, то p* является таким же, как и распределение суммарного числа успехов, т.е. биномиальным.

Математическое ожидание и среднее квадратическое отклонение биномиального распределения соответственно равны:

; , тогда

оценка является несмещённой.

, где p – вероятность успеха, q=1-p – вероятность неудачи одного испытания Бернулли.

Когда n возрастает, биномиальное распределение стремится к нормальному.

Распределение относительной частоты p* можно приближённо считать нормальным распределением со средним значением p и средним квадратическим отклонением , если и .

Пример.

Среди определённой категории людей 10% предпочитают отдыхать на даче. Случайно выбраны 100 человек из этой категории людей. Какова вероятность того, что не менее 5% из них проведут отпуск на даче?

Решение.

Требуется найти вероятность того, что . По условию p=0,1; объём выборки n=100. Т.к. , , то распределение p* можно приближённо считать нормальным с ; . Искомая вероятность равна площади под графиком нормального распределения, лежащей правее вертикали x=0,05.