Глава 3. Многомерные случайные величины.

§1. Понятие о многомерных случайных величинах.

Случайный опыт характеризуется, как правило, не одной, а несколькими случайными величинами. Например, состояние газа в сосуде определяется давлением и температурой. При изготовлении труб контролируется внутренний диаметр и внешний диаметр. Многие экономические показатели являются многомерными случайными величинами, например, уровень жизни населения:

- ВНП на душу населения

- распределение доходов

- продолжительной жизни

- экологические факторы

- издержки предприятий: постоянные и переменные

Определение: говорят, что задана многомерная случайная величина или n-мерный случайный вектор X=(X₁,X₂,…,X_n). Если на одном и том же вероятностном пространстве (E,K,P) задано n случайных величин:

X₁(e), X₂(e), …, X_n(e)

Мы будем рассматривать двумерную случайную величину (X,Y). Геометрически будем её использовать как случайную точку M(X,Y) на плоскости или как случайный вектор на плоскости.

К ак и в одномерном случае, закон распределения двумерной случайной величины определяется функцией распределения , которая является числовой функцией двух переменных и как вероятность принимает значения на отрезке [0,1].

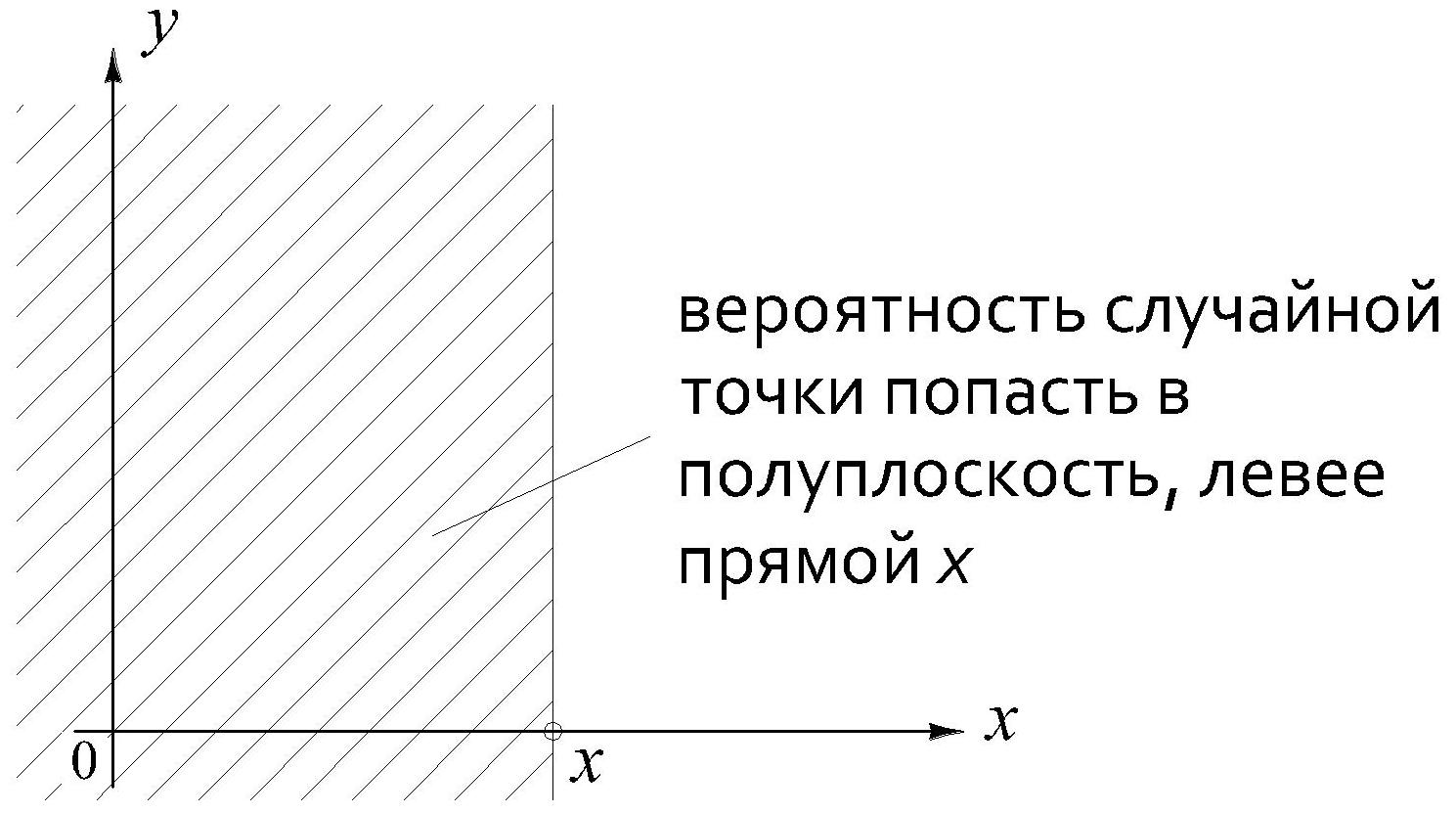
Геометрически – это вероятность того, что случайная точка попадает в бесконечный квадрат с вершиной в точке (x,y), расположенный левее и ниже этой вершины.

Свойства F(x,y).

1. F(x,y) – неубывающая:

F(x₂,y)≥F(x₁,y), если x₂>x₁

F(x,y₂)≥F(x,y₁), если y₂>y₁

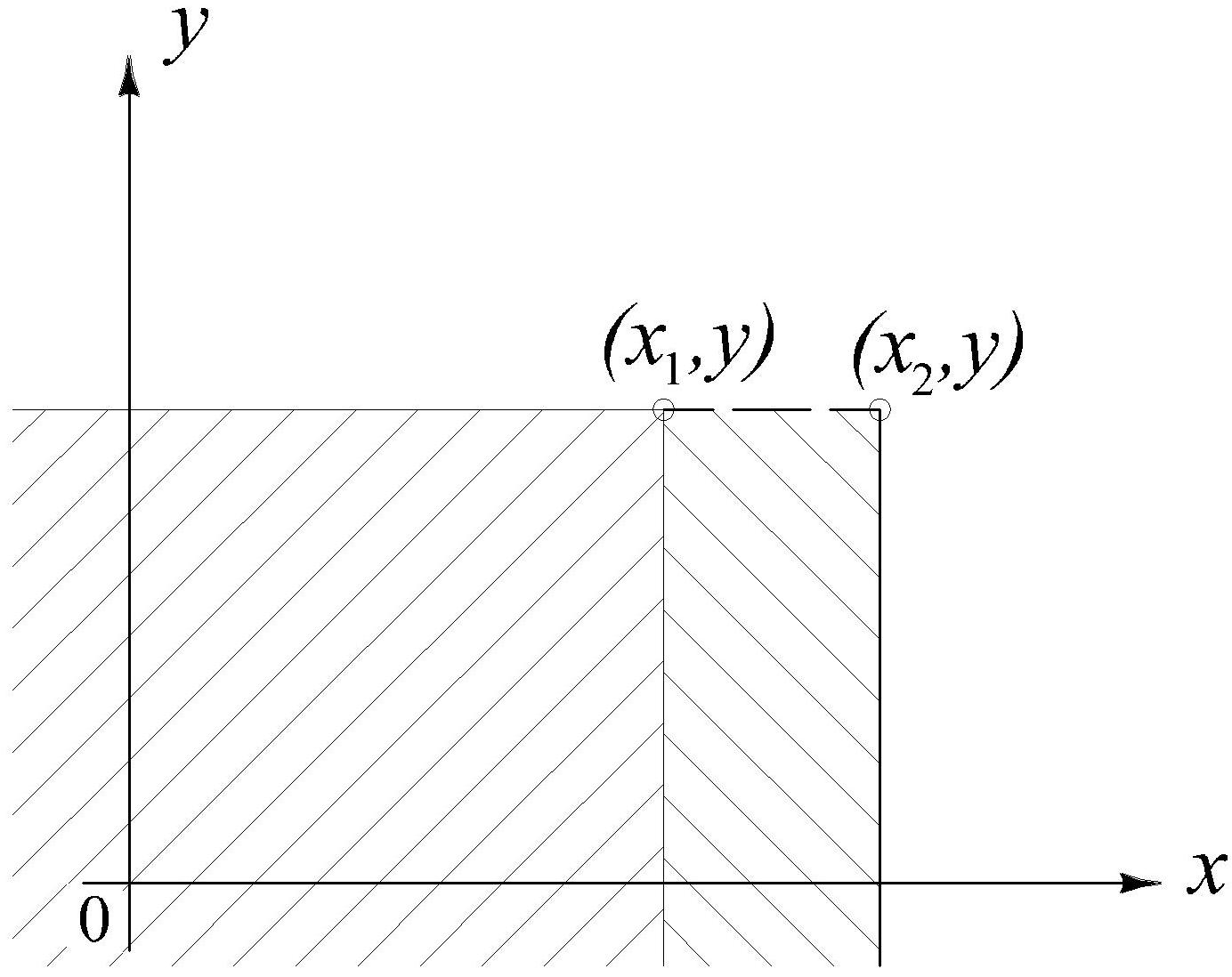
Вероятность попадания в квадрант с вершиной (x₂,y) не может уменьшиться.

2. F(+∞,+∞)≥1. Квадрант с вершиной (x,y) при , обращается во всю плоскость XoY, попадание в которую случайной точки – есть достоверное событие.

3. F(-∞,y)=F(x,-∞)=0.

Частные законы распределения. Независимость случайных величин.

Дана двумерная случайная величина (X,Y) и F(x,y) – функция распределения.

F(x,y) – функция распределения.

F(x,y) – вероятность того, что .

, .

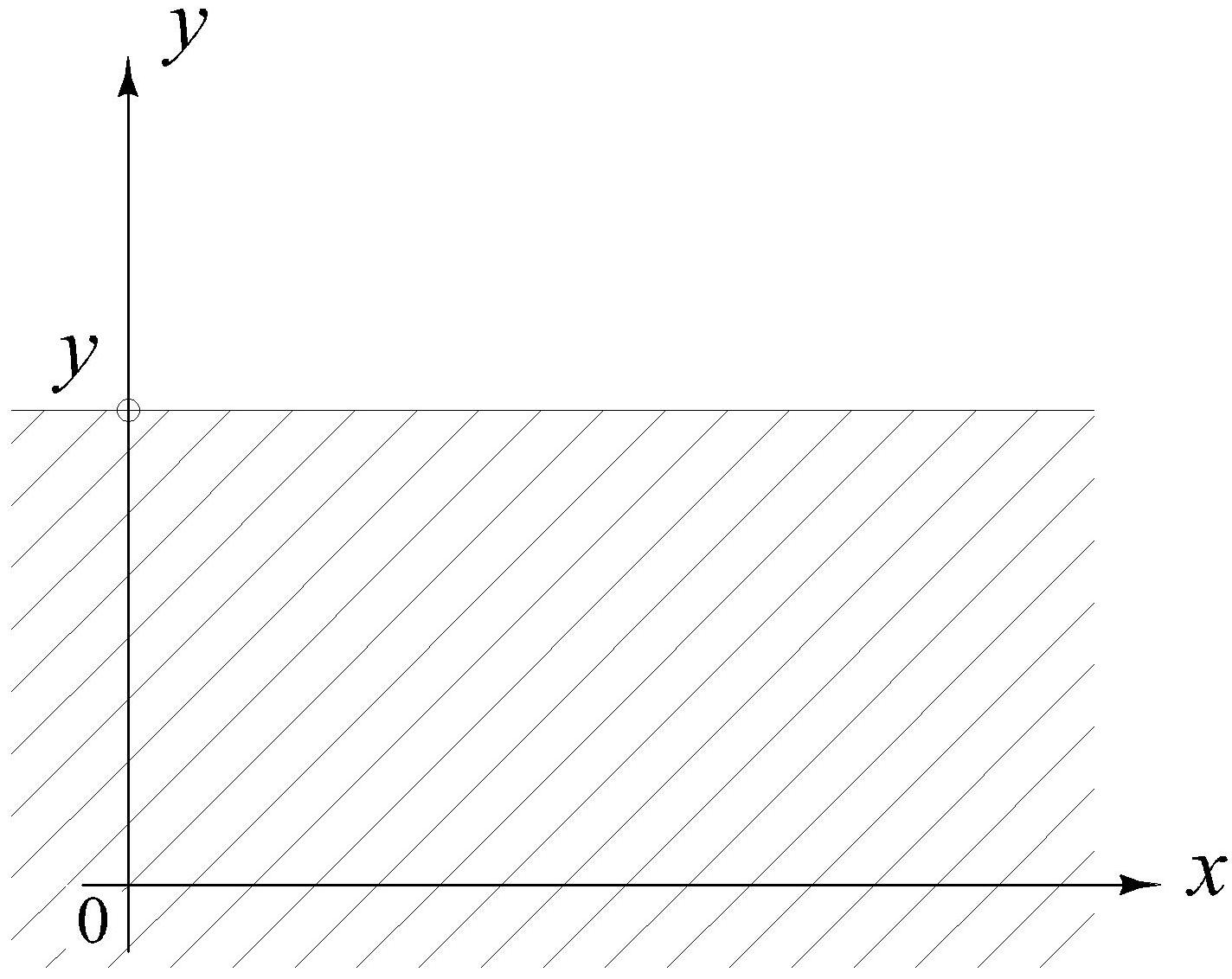
Говорят, что функция F(x,y) задаёт совместный закон распределения случайных величин X и Y, а функции F₁(x) и F₂(y) – частные законы распределения составляющих X и Y. Зная совместный закон, можно определить частные распределения.

Определение. Случайные величины X и Y называются независимыми, если для любых действительных x и y выполняется равенство . Для случая независимого распределения по частным распределениям мы можем выставить совместный закон распределения.

§2. Дискретная двумерная случайная величина.

Случайная величина (X,Y) называется дискретной, если дискретны обе её составляющие.

Обозначим x_i – возможные значения случайной величины X, i=1,2,…,n; обозначим y_j – возможные значения случайной величины Y, j=1,2,…,m. Тогда возможные значения двумерной случайной величины – это пары вида . Обозначим , , P_ij≥0.

Закон распределения дискретной двумерной случайной величины задаётся с помощью таблицы, которая имеет 2 входа:

X Y	x1	x2	…	xi	…	xn
y1	P11	P21	…	Pi1		Pn1
y2	P12	P22	…	Pi2	…	Pn2
…
yj	P1j	P2j	…	Pij	…	Pnj
…
ym	P1m	P2m	…	Pim	…	Pnm

Вероятности P_ij задают совместный закон распределения.

Эти вероятности задают частные распределения. Выясним, как выражаются частные законы распределения через совместные.

X=x_i, т.к. события , , …, несовместны, то по аксиоме сложения вероятностей .

Аналогично, .

Дискретные случайные величины X и Y называются независимыми .

Мы знаем, что если события A и B являются зависимыми, то условная вероятность события B отличается от его безусловной вероятности: .

Для характеристики зависимости между составляющими двумерной случайной величины вводят понятие условного распределения. Условным распределением составляющей X при Y=y_j называют , , …, . Все эти вероятности вычисляются в предположении, что событие Y=y_j уже наступило.

Зная совместный закон распределения двумерной дискретной случайной величины, можно определить условные законы распределения составляющих:

, .

Пример.

Дан закон распределения двумерной случайной величины. Выяснить, являются ли X и Y независимыми случайными величинами.

X Y	1	2	3
1
2
3

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

, , ,

дискретные случайные величины X и Y – независимы.

Ответ: случайные величины X и Y – независимы.