Замена переменной в неопределенном интеграле.

Основную роль в интегральном исчислении играет формула замены переменных (или подстановки) (1).

В этой формуле предполагается, что есть непрерывно дифференцируемая функция на некотором интервале изменения , а - непрерывная функция на соответствующем интервале или отрезке оси . Докажем это утверждение. Слева в (1) стоит функция, которая является первообразной от . её производная по равна:

Следовательно, если ввести в этой функции подстановку , то получится первообразная от функции . Интеграл же справа есть, по определению, некоторая первообразная от . Но две первообразные для одной и той же функции отличаются на некоторую постоянную . Это и записано в виде первого равенства (1). Что касается второго, то оно носит формальный характер - мы просто уславливаемся писать:

Пример: .

Билет 29

Интегрирование простейших рациональных дробей

1.

2.

4.

5 .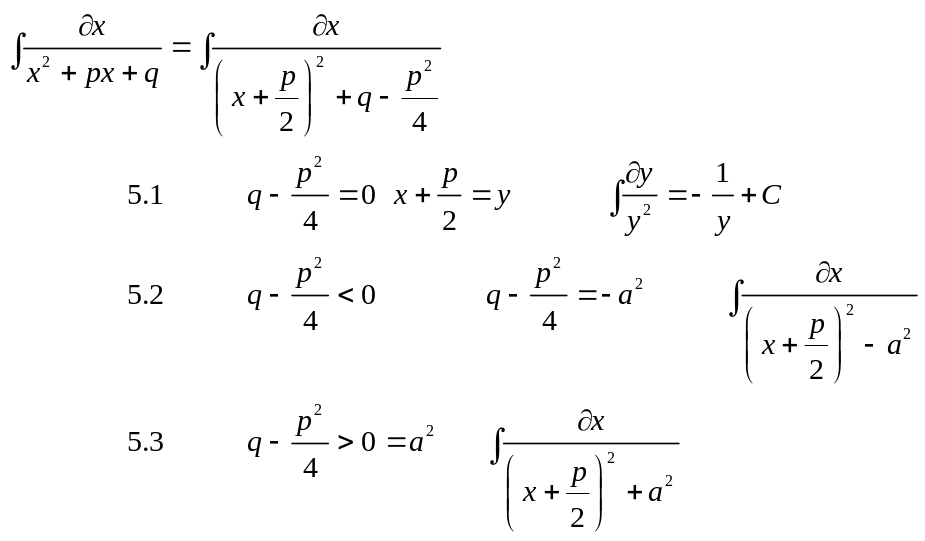

рассмотрено в пункте 3

рассмотрено в пункте 4.

6.

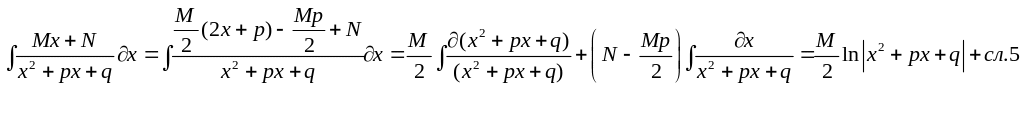
7.

8. -случай 7

9. Случай 8.

Билет 30

Интегрирование рациональных дробей.

Пусть нужно найти неопределенный интеграл от рациональной действительной дроби. Если степень многочлена P k не меньше степени многочлена Q n ( ), то прежде всего разделим P на Q :

Многочлен R интегрируется без труда, а – правильная действительная дробь. Все трудности сводятся к интегрированию правильной дроби, которую мы снова обозначим через и представим в виде:

Тогда пусть ,

1 случай.

Знаменатель содержит простые действительные корни, тогда его можно разложить на простейшие множители: (см.Теор.1)

. Тогда

Приравнивая тождественно равные числители, получим:

Существуют 2 метода нахождения :

1. сравниваем коэффициенты при x с одинаковыми степенями; однако этот метод очень трудоемкий.

2. Т.к. равенства тождественны, можем взять , тогда . Так, подставляя поочередно 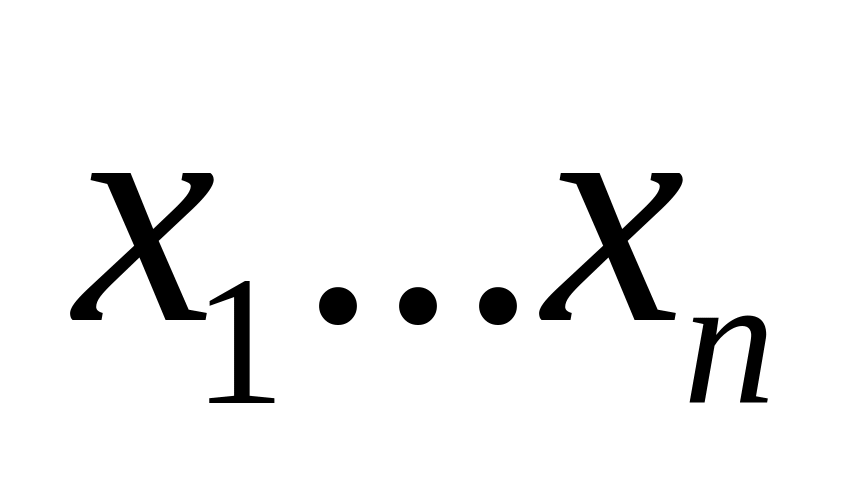найдем все

Т.о., мы получили сумму элементарных дробей, которые можем легко проинтегрировать.

Пример

2 случай.

Знаменатель содержит кратные корни, тогда его можно представить в виде:

.

Пусть существуют n различных корней с кратностями , тогда

- и делаем все так же, как и в предыдущем примере.

Пример

3 случай.

Знаменатель содержит кратные корни и многочлены, имеющие комплексные корни;

, где многочлены , имеют комплексные корни.

Тогда R(x) представим в виде:

Снова приводим к общему знаменателю и приравниваем числители.

Пример

4 случай

Знаменатель содержит кратные действительные и кратные комплексные корни;

Тогда R(x) представим в виде:

А дальше все делаем по старой схеме: методом неопределенных коэффициентов находим A, B...

Пример

Теорема 1

Любой многочлен над полем С раскладывается на линейные и квадратичные множители с действительными коэффициентами:

Доказательство

Если , то все в порядке: - линейный множитель с вещественными коэффициентами

Пусть тогда существует невещественный корень . Ему соответствует скобка .

Тогда если – корень, то сопряженный к нему тоже будет корнем. Тогда наряду с множителем будет присутствовать множитель . Перемножим эти 2 скобки: - квадратный трехчлен с вещественными коэффициентами, что и требовалось доказать.

Теперь нам нужно доказать, что любые правильные дроби раскладываются на простейшие.

Лемма 1

Пусть многочлен представим в виде: , где - выделили максимальное кол-во скобок (x-a)

и - степень числителя меньше степени знаменателя, тогда

, причем дробь - правильная; если , то ; M(x) – многочлен с действительными коэффициентами.

Доказательство

Действуем так же, как в примерах: приводим к общему знаменателю и приравниваем числители:

; подставим , тогда , по условию

- нам нужно доказать, что это – многочлен, а не дробь. Подставим x=a, числитель при такой подстановке = 0, а это значит, что многочлен делится на , т.е. M(x) – многочлен с действительными коэффициентами.

Теперь докажем, что дробь - правильная, т.е. что .

Степень знаменателя дроби = n-1, для числителя ( M(x)): по условию и , да еще делим на (x-a) ( ), значит - меньше степени знаменателя, что и требовалось доказать.

Лемма 2

Если многочлен Q(x) имеет комплексный корень кратности k, т е представим в виде , при этом многочлен имеет только комплексные корни, которые не являются корнями N(x). , тогда дробь можно представить в виде:

, причем вторая дробь будет правильной. M(x) – многочлен с действительными коэффициентами.

Доказательство

Снова приведем дробь к общему знаменателю и приравняем числители. Получим

Пусть , - корень многочлена , , значит сопряженное к нему тоже корень. Подставим и :

; Найдем определитель системы, чтобы выяснить, имеет она решения, или нет:

, значит, система разрешима и существуют A и B – решения системы, нужно доказать, что

, заменим A и B на : , решим сопряженную систему: - получили исходную систему;

так как столбец - решение, столбец является решением. А т.к. решение должно быть единственным (определитель ), ; M(x) находится аналогично Лемме 1 ; теорема доказана.

Обобщая все вышесказанное, получаем: («Теорему о разложении на простейшие дроби»)

Пусть многочлен представим в виде: и положим , тогда

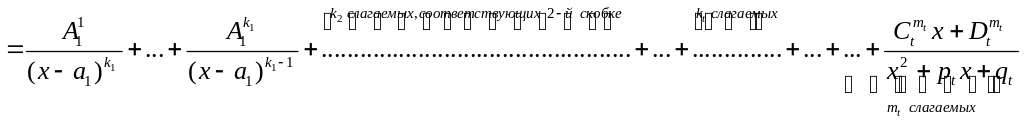
Заметим, что в самой последней дроби степень числителя (первая) меньше степени знаменателя (вторая) , т.е. последняя дробь – правильная. И каждую из дробей-слагаемых мы можем проинтегрировать в элементарных функциях.

Общий вывод: Любая рациональная дробь интегрируется в элементарных функциях.

Билет 31