4.Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Формулы Крамера.

Системой m линейных алгебраических уравнений с n  неизвестными называется система уравнений вида:

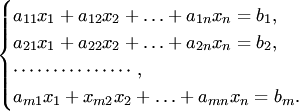Числа а_ij-коэффициенты системы,б₁-свободные члены,х-неизвестные.

Решением системы называется упорядоченная совокупность n чисел (α₁,α₂,…,α_n) такая, что после замены неизвестных x₁,x₂,…,x_n соответственно числами α₁,α₂,…,α_n  каждое уравнение системы превращается в верное числовое равенство. Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной. Система называется однородной, если все свободные члены равны нулю:

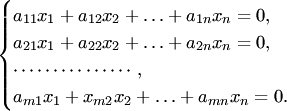
Решить систему-выяснить совместная она или нет ,и, если совместная, то найти все ее решения.

Элементарные преобразования линейной системы:

1)умножение уравнения системы на ненулевое число 2)прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число

3)перестановка местами двух уравнений системы

4)вычеркивание уравнения, все коэффициенты которого равны 0

Теорема Кронекера-Капелли -для совместности системы линейных алгебраических уравнений необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.

Следствие:если ранг матрицы системы меньше ранга ее расширенной матрицы,то такая система несовместна.

Формула Крамера

Если определитель   матрицы системы n линейных уравнений с n неизвестными отличен от нуля, то система имеет единственное решение, которое находится по формулам

-это правило справедливо для невырожденных систем.

Пример:

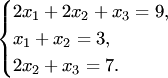
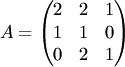
Решение. Составим матрицу системы Вычислим ее определитель: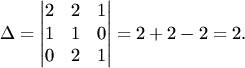

Так как определитель отличен от нуля, система имеет единственное решение .Находим определители  и неизвестные  

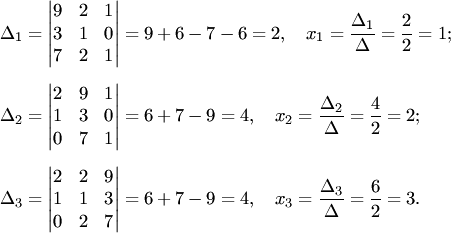
5.Метод Гаусса решения систем линейных алгебраических уравнений.

Если ранг матрицы совместной системы равен количеству неизвестных ,то система имеет единственное решение.

Если же ранг матрицы совместной системы меньше количества неизвестных, то система имеет бесчисленное множество решений.

Рассмотрим систему линейных уравнений S. Метод Гаусса решения систем линейных уравнений состоит из двух этапов, называемых прямым и обратным ходом. Прямой ход метода Гаусса заключается в том, что с помощью элементарных преобразований  над расширенной матрицей система S приводится к «ступенчатому» виду.

Обратный ход метода Гаусса состоит в том, что, начиная с последнего уравнения ступенчатой системы, вычисляются неизвестные.

При реализации прямого хода метода Гаусса возможны следующие три случая:

1. В результате преобразований в системе уравнений будет получено уравнение вида a*0+b*0+c*0=d где d 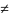0  Ясно, что никакой набор действительных чисел этому уравнению удовлетворять не может, поэтому в таком случае система уравнений несовместна.

2. В результате преобразований получится ступенчатая система уравнений

в которой количество уравнений совпадает с количеством неизвестных.     

В этом случае система уравнений является определённой.

В результате преобразований получится система уравнений ступенчатого вида, в которой количество неизвестных больше числа уравнений системы (m>n)

В этом случае те неизвестные, которые стоят на «ступеньках», называются главными неизвестными (x_n), а другие неизвестные называются свободными (X_n+1); система уравнений будет неопределённой. Тогда обратный ход метода Гаусса состоит в том, что начиная с последнего уравнения системы, главные неизвестные выражаются через свободные и составляется общее решение системы уравнений. Для того чтобы получить какое-либо частное решение системы, свободным неизвестным придают конкретные числовые значения, вычисляя тем самым главные неизвестные.

Решить:

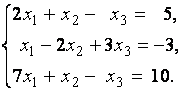
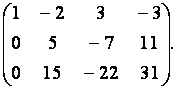
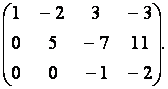
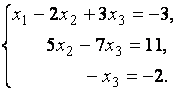
Ответ 2,5,1

Векторы в декартовой системе координат.

Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат (в честь французского математика Рене Декарта).

Декартова система координат в пространстве определяется точкой и базисом из трех векторов. Точка O называется началом координат. Прямые, проведенные через начало координат в направлении базисных векторов, называются осями координат. В трехмерном пространстве они называются осями абсцисс, ординат и аппликат. Оси координат являются числовыми осями с началом в точке O , положительным направлением, совпадающим с направлением соответствующего базисного вектора, и единицей длины, равной длине этого вектора. Координатами точки M называются координаты вектора OM (радиус–вектора) Если базис ортонормированный, то связанная с ним декартова система координат называется прямоугольной.

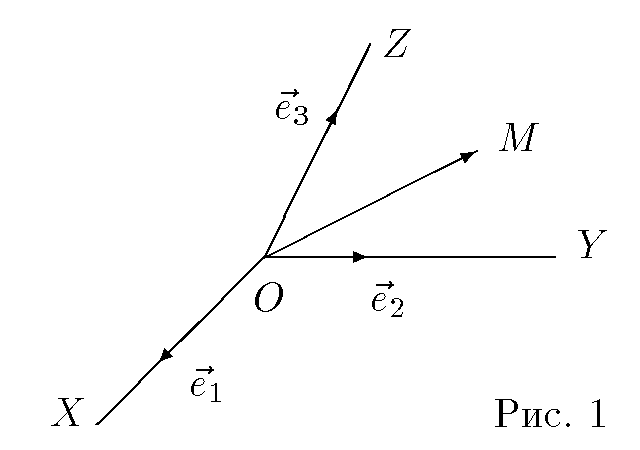
Положение точки M на плоскости в прямоугольной системе координат определяется так.Проводим MP||Y`Y до пересечения с осью X`X в точке P иMQ||X`X до пересечения с осью Y`Y в точке Q. Числа x и y измеряющие отрезкиOP и OQ в выбранном масштабе называются —Прямоугольные координаты точки M.

Связанным вектором 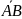с началом в точке А и концом в точке B называют направленный отрезок AB,в котором точка А является началом,а точка B-концом.Начало вектора называют еще точкой его приложения.

Если для направленного вектора АБ фиксируется только длина и направление,то он называется свободным вектором.

Координатами вектора 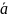  называются проекции а_x и a_y данного вектора на оси O_x и O_y соответственно:

Величина a_x называется абсциссой вектора , а число a_y - его ординатой.

Длиной (модулем) вектора   называется неотрицательное число, равное расстоянию между его началом и концом, то есть длина вектора - это длина отрезка AB. Длина   обозначается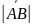 

Длина вектора, заданного координатами, равна корню квадратному из суммы квадратов его координат.

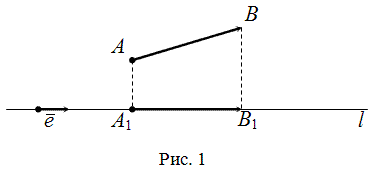
Проекцией вектора на ось l называется длина отрезка A₁B₁, взятая со знаком "+", если направление   совпадает с направлением вектора 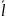 , и со знаком "-", если направление  противоположно направлению единичного вектора оси l.

Сложение векторов 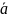и 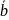осуществляется по правилу треугольника.

Суммой 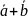двух векторов и называют такой третий вектор , начало которого совпадает с началом , а конец - с концом при условии, что конец вектора и начало вектора совпадаюt.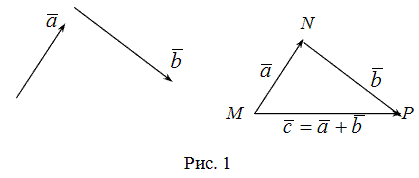

Разностью 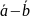векторов и называется вектор такой, что выполняется условие:

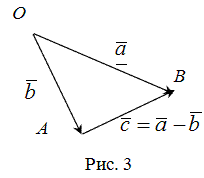
Произведением α называют вектор, который коллинеарен вектору ,имеет длину, равную 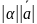,и направление такое же, как и вектор ,если α>0, и противоположное, если α<0.

Линейной комбинацией векторов называется выражение вида: ,где - произвольные числа.

Пример:

Ненулевые векторы называются линейно независимыми, если только тривиальная линейная комбинация(все коэфф.равны0) этих векторов равна нулевому вектору.

Пример:

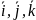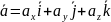Теорема: Любой вектор можно единственным образом разложить по базису , т.е. представить в виде ,где 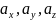-числа.

Тройка векторов называется базисом.

Векторы 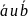называются коллинеарными(параллельными),если они лежат на одной прямой или на параллельных прямых, при этом пишут

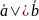
Вектор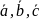ы называют компланарными, если существует плоскость, которой они параллельны