1. Матрицы. Операции над матрицами. Ранг матрицы.

2. Определители и их свойства.

3. Обратная матрица. Матричный метод решения невырожденных систем линейных алгебраических уравнений.

4. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли. Формулы Крамера.

5. Метод Гаусса решения систем линейных алгебраических уравнений.

6. Векторы в декартовой системе координат.

7. Скалярное, векторное и смешанное произведения векторов.

8. Прямая на плоскости.

9. Эллипс, гипербола и парабола. Их характеристики.

10. Упрощение общего уравнения кривых второго порядка на плоскости.

11. Плоскость. Взаимное расположение плоскостей. Расстояние от точки до плоскости.

12. Прямая в пространстве. Взаимное расположение двух прямых в пространстве.

13. Прямая и плоскость в пространстве. Взаимное расположение прямой и плоскости.

14. Общее уравнение поверхности второго порядка. Поверхности вращения. Конические поверхности. Цилиндрические поверхности.

15. Эллипсоид. Гиперболоиды. Параболоиды.

16. Множества и действия над ними. Метод математической индукции. Верхняя и нижняя грани числового множества.

17. Предел числовой последовательности.

18. Предел функции.

19. Замечательные пределы. Эквивалентные функции и их применение к вычислению пределов.

20. Непрерывность функции в точке и на отрезке. Обратная функция и её непрерывность.

21. Точки разрыва функции и их классификация. Непрерывность элементарных функций.

22. Производная функции, её геометрический и физический смысл.

23. Правила дифференцирования, производная сложной и обратной функции. Дифференцирование функций, заданных параметрически и неявно. Производные высших порядков.

24. Дифференциал функции и его геометрический смысл. Дифференциалы высших порядков.

25. Теоремы Ролля, Лагранжа и Коши. Правило Лопиталя.

26. Формула Тейлора.

27. Экстремумы функции. Выпуклость и точки перегиба. Асимптоты графика функции.

28. Кривизна плоской кривой. Понятие об эволюте и эвольвенте.

29. Векторная функция скалярного аргумента.

30. Касательная прямая и нормальная плоскость к пространственной кривой. Кривизна и кручение пространственной кривой. Формулы Френе.

31. Линейное векторное пространство. Евклидово пространство.

32. Линейные операторы. Собственные векторы и собственные значения матриц.

33. Квадратичные формы и их матрицы. Применение квадратичных форм к исследованию кривых и поверхностей второго порядка.

34. Комплексные числа.

35. Алгебраические многочлены. Разложение рациональных функций на простейшие дроби.

36. Неопределённый интеграл. Методы интегрирования.

37. Интегрирование простейших рациональных функций и выражений, содержащих простейшие иррациональные функции.

38. Интегрирование выражений, содержащих тригонометрические функции.

39. Определённый интеграл.

40. Интеграл с переменным верхним пределом и его дифференцирование.

41. Несобственные интегралы первого и второго рода.

42. Приложения определённого интеграла.

1.Матрицы.Операции над матрицами

Матрица-прямоугольная таблица чисел из множества R.Матрица А называется квадратной, если m=n. В общем случае матрица называется прямоугольной с размерами m*n и обозначается А_m*n.

Матрицы A и Bназываются равными, если они имеют одинаковые размеры и их соответствующие элементы равны(a_ij=b_ij)

Если все элементы матрицы равны 0,то матрица называется нулевой и обозначается 0.

Главной диагональю квадратной матрицы называют совокупность ее элементов a₁₁,a₂₂,…,a_nn , а побочной диагональю-a_n1,a_n-1,a_1n. Матрица D,у которой все элементы, расположенные вне главной диагонали равны 0 называется диагональной и обозначается D= .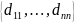

В случае, если все элементы диагональной матрицы равны 1,то она называется единичной матрицей.

Треугольная матрица-матрица, в которой все элементы, расположенные с одной стороны от главной диагонали равны 0(в верхней треугольной снизу главной диагонали лежат нули, а в нижней треугольной наоборот).

Трапециевидной называют матрицу вида:

Суммой двух матриц A и B одинаковых размеров называется матрица С тех же размеров, каждый элемент которой равен сумме соответствующих элементов матриц A и B.

, ,

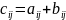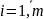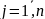
Произведением матрицы А на число α€R называется матрица С,каждый элемент которой есть произведение соответствующего элемента матрицы А и числа альфа.

Свойства:

1)(AB)C=A(BC)

2)(A+B)C=AC+BC

3)A(B+C)=AB+AC

Если AB=BA,то матрицы A и B называют перестановочными матрицами.Пример:

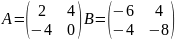
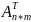к матрице А_m*n-это матрица, полученная из матрицы А после замены строк одноименными столбцами.

Рангом матрицы А назовем наибольший порядок не равного нулю его минора

Свойства:

1. Для матрицы А_m*n справедливо 0<=rank(a)<=min(m,n)(меньшее из чисел m и n

2. Равенство r(A)=0 справедливо тогда и только тогда,когда А-нулевая матрица 0

3. Для квадратной матрицы А порядка n имеем r(A)=n тогда и только тогда,когда А-невырожденная матрица.

4. Ранг транспонированной матрицы равен рангу соответствующей ей нетранспонированной матрицы.

5. Ранг матрицы, полученной из исходной вычеркиванием какого-либо столбца или стоки,равен рангу исходной матрицы или меньше его на единицу.

6. Ранг матрицы,полученной из данной матрицы в результате приписывания к ней произвольного столбца либо строки,равен рангу исходной матрицы или больше его на единицу

7. Если к матрице дописать или вычеркнуть нулевой столбец(нулевую строку),ранг полученной матрицы равен рангу исходной.

Нахождение ранга матрицы:

Если все миноры первого порядка, т.е. элементы матрицы А равны 0,то r=0.В случае, когда есть хотя бы один ненулевой элемент матрицы, рассмотрим миноры второго порядка, включающие в себя этот элемент. Если все они равны 0,то r=1.При наличии хотя бы одного ненулевого минора второго порядка рассмотрим третьего порядка и т.д. Этот процесс продолжим до тех пор, пока не станет ясно , что все миноры порядка k+1 равны 0 или уже не существуют. Тогда получим, что k=r

_­Пример:

А=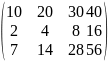 Все миноры 2порядка равны нулю(все элементы пропорциональны)Миноры первого порядка равны отличны от нуля.Ранг равен 1.