13.Оптимальное число линий в системах с отказом

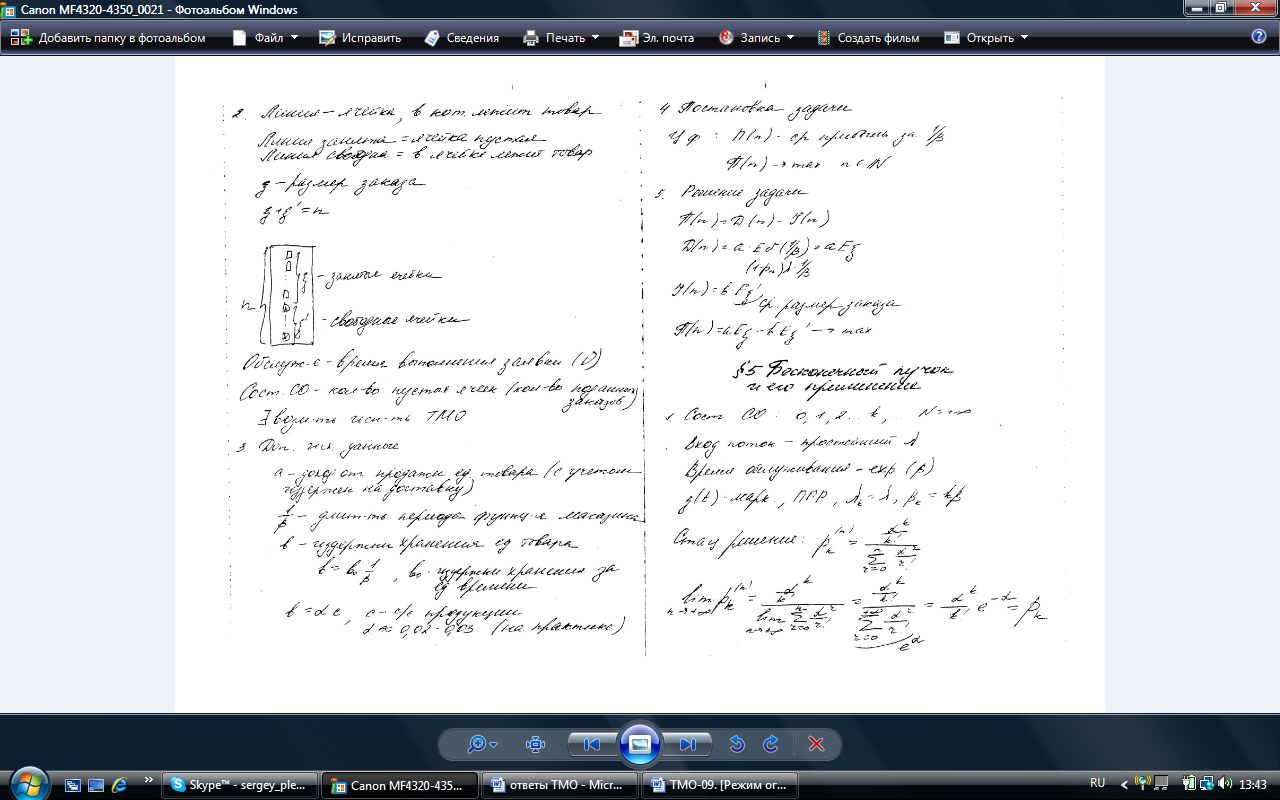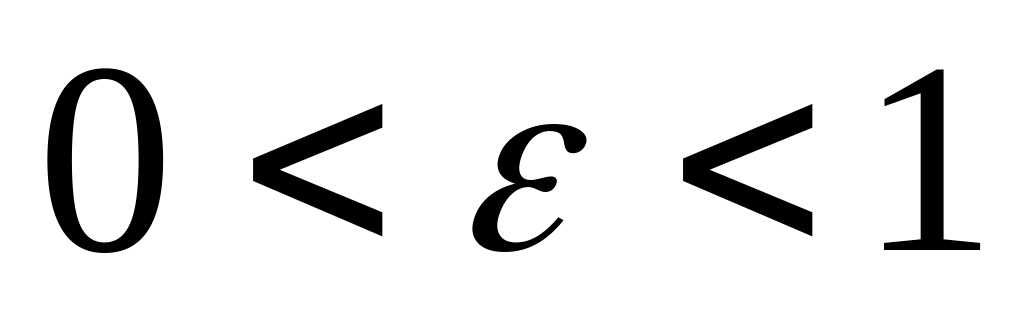1. Пусть задается уровень обслуживания - максимальное значение доли вызовов, которые могут получать отказ в данной системе обслуживания. . Пусть , это значит, что не больше 10% вызовов могут получать отказ.

2. Пусть a – средняя плата за обслуживание

b – штраф за отказ в обслуживании

с – оплата труда линии за единицу времени ее работы

Средняя прибыль за ед. времени: .

3. .

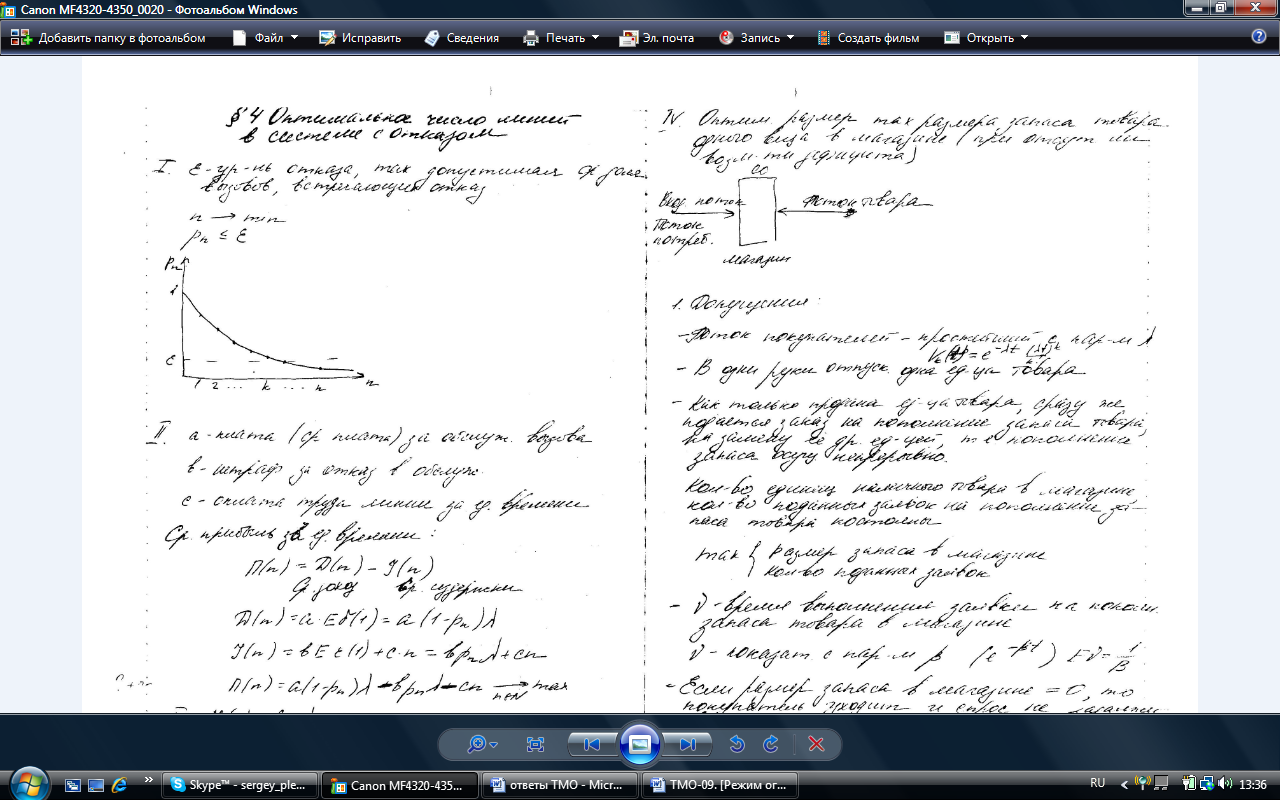
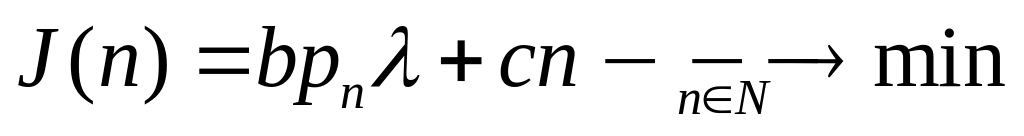4. Оптимальный размер максимального числа товаров одного вида в магазине при отсутствии возможности дефицита.

1. Допущения

1. Поток покупателей является простейший с параметром ( - человек в неделю)

2. В одни руки отпускается только одна единица товара => - вероятность того, что спрос будет предъявлен за t единиц времени на k единиц товара.

3. Как только происходит продажа единиц товара, сразу подается заявка на замену ее другой единицей => [количество товара в магазине + количество заявок] = = n. n можно понимать либо как максимальный размер товара, либо как максимальное количество заявок.

4. Время выполнения заявок - непрерывная случайная величина, распределенная по показательному закону с параметром .( ),

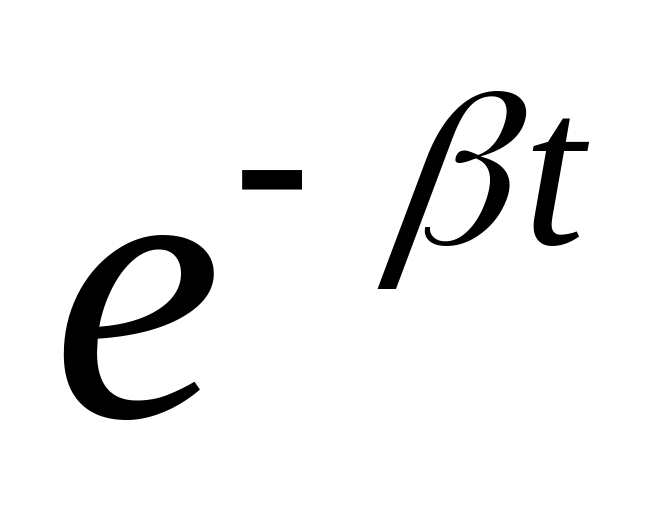5. Если товар в магазине отсутствует, то покупатель получает отказ и уходит.

2. Линия – ячейка, в которой лежит товар.

Линия занята – ячейка пуста,

Линия свободна – ячейка заполнена

Всего n линий

– размер заказа.

Обслуживания – время выполнения заявки ( )

Состояние СО – количество пустых ячеек (количество поданных заказов).

3. Дополнительные исходные данные

Пусть а – доход от продажи единицы товара за вычетом издержек выполнения заказа по доставке товара в магазин. b – издержки хранения единицы товара в течение промежутка времени .

– издержки хранения за единицу времени

, где с – себестоимость,

4. Постановка задачи: 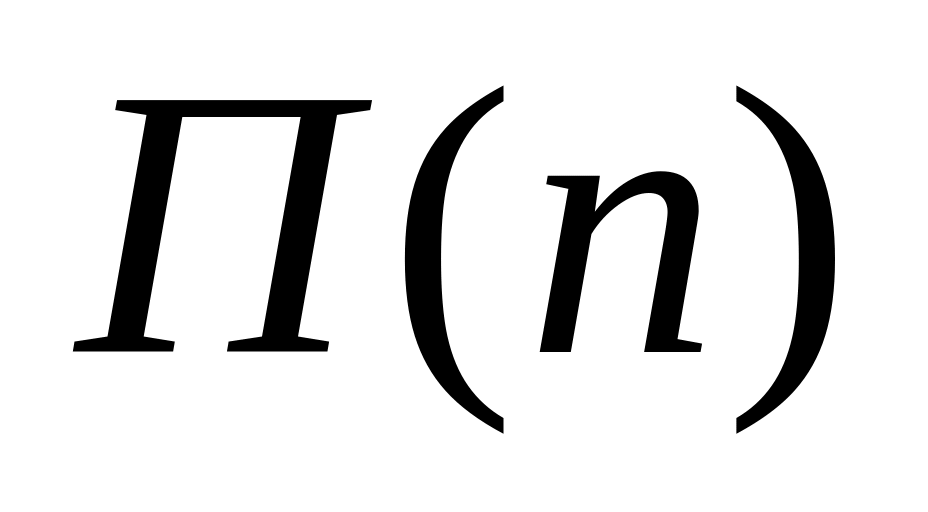- средняя прибыль за .

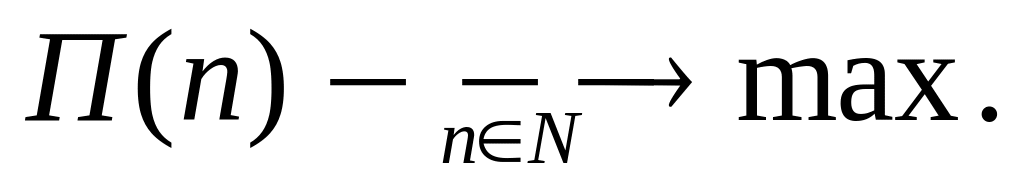
5. Решение задачи

.

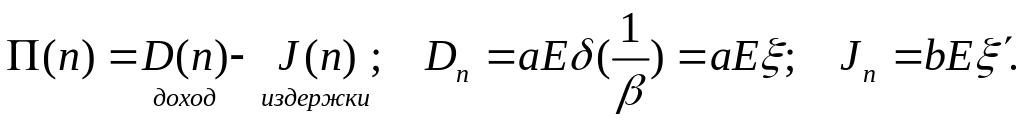
14.Бесконечный пучок и его практические приложения

Бесконечный пучок – пучок, в котором количество линий не ограничено.

1. Сост(ояния) CO: 1,2, ….k,

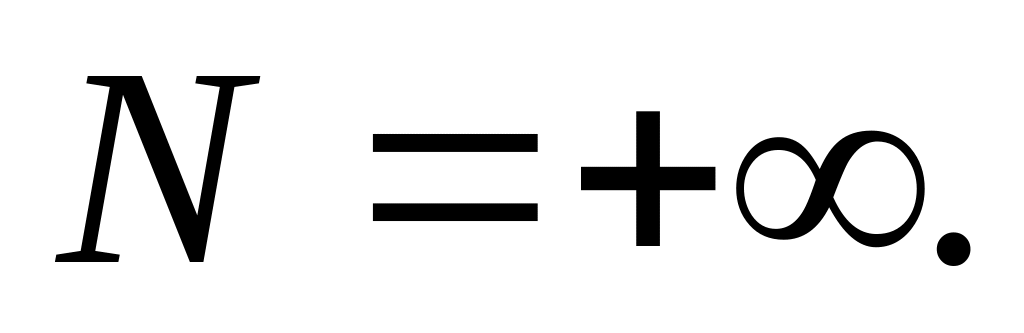
Входящий поток – простейший, Время обслуживания –

– марковский, ПГР,

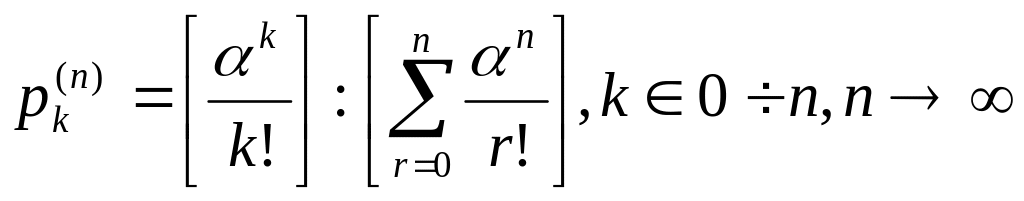
, . – стац. реш-ие для беск. пучка.

Следствия: 1. Стац. решение распределено по закону Пуассона с параметром . 2 - показатель эффективности.

Замечание: Стационарное решение справедливо для распределения длины разговора.

2. Приложения:

1. Доставка телеграмм. СО – телеграф, линия – почтальон, доставляющий телеграмму, пучок линий – совокупность почтальонов, обслуживание - доставка. Поток телеграмм - простейший с параметром за t поступает ровно k телеграмм с вероятностью , ( .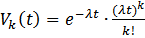

Допущения: 1)Каждый почтальон доставляет одновременно только одну телеграмму.

2. Каждая телеграмма начинает доставляться немедленно по ее получении телеграфом. – время доставки телеграммы и возврата почтальона – случайная величина (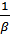 - среднее время доставки.) Вероятность того, что в пути находится одновременно k почтальонов, .

2. Ремонт автомашин. СО – совокупность ремонтных мастерских. Вызов – автомашина, требующая ремонта. Обслуживание – ремонт. Пусть ремонт начинается немедленно по выходу машины из строя. Поток поломок – простейший с параметром . ; - среднее время ремонта автомашины.