7.Свойства показательного распределения разговора
Пусть - длина разговора - случайная величина, >0;
-
функция распределения для
.
- вещественное число
– “возраст” разговора к данному моменту
-
“остаток” разговора после момента
,
случайная величина
- функция распределения
(
)
– вероятность того, что разговор,
длившийся уже а единиц времени, продлится
ещё >t единиц времени.
при
:
- безусловная вероятность,
при
:
- условная вероятность.
Теорема(Свойство показательного закона):
Для того, чтобы остаток разговора был распределен также как и весь разговор , необходимо и достаточно, чтобы закон распределения являлся показательным.
~
Доказательство:
Достаточность.
;
,
не
зависит от
не зависит от
.
Следовательно,
.
Ч.т.д.
Замечания:
1.
~
-беск.мало
А) Если функции
распределений случайных величин
совпадают, то такие случайные величины
отождествляются.
~
.
Тогда
- семейство случайных величин, зависящих
от
- случайный процесс.
Показательный
закон играет исключительную роль среди
всех законов распределения – только
при показательном законе распределения
остаток ведет себя так же, как и весь
разговор.
,
в момент
вероятность закончиться у обоих
разговоров
Б)
~
- часть ведет себя как целое.
В)
~
-беск.мало
2. Физический смысл показательного закона.
Длина разговора является бесконечно малой величиной. Большинство вызовов нуждается в кратковременном (близком к 0) обслуживании. Поскольку в реальности дело обстоит не так, эта предпосылка неверна. Тем не менее, предполагаем закон распределения показательным.
Со временем от этой
предпосылки удалось отказаться.
3. Физический смысл
параметра
:
:
- средняя длина разговора;
- интенсивность обслуживания вызовов
на линии. Среднее число вызовов, которое
происходит в ед. времени
- пропускная способность для СО
4. Расчет (или 1/ ) в показательном законе.
А) Наблюдаем за случайной величиной
Б) Регистрируем ее
реализации
-фактическое
время реализации в i-ом наблюдении.
В)
.
8.Марковость в задаче Эрланга
Если входящий поток в
данную СО – простейший, время обслуживания
распределено по показательному закону,
то случайный процесс
(сост. СО на t) является Марковским.
Доказательство:
Рассмотрим T- любой
момент времени,
-
сост. СО на T,
.
3 Фактора, определяющих :
М
оменты
окончания тех разговоров, которые
ведутся в момент T. Имеет место
независимость от прошлого и от возраста.
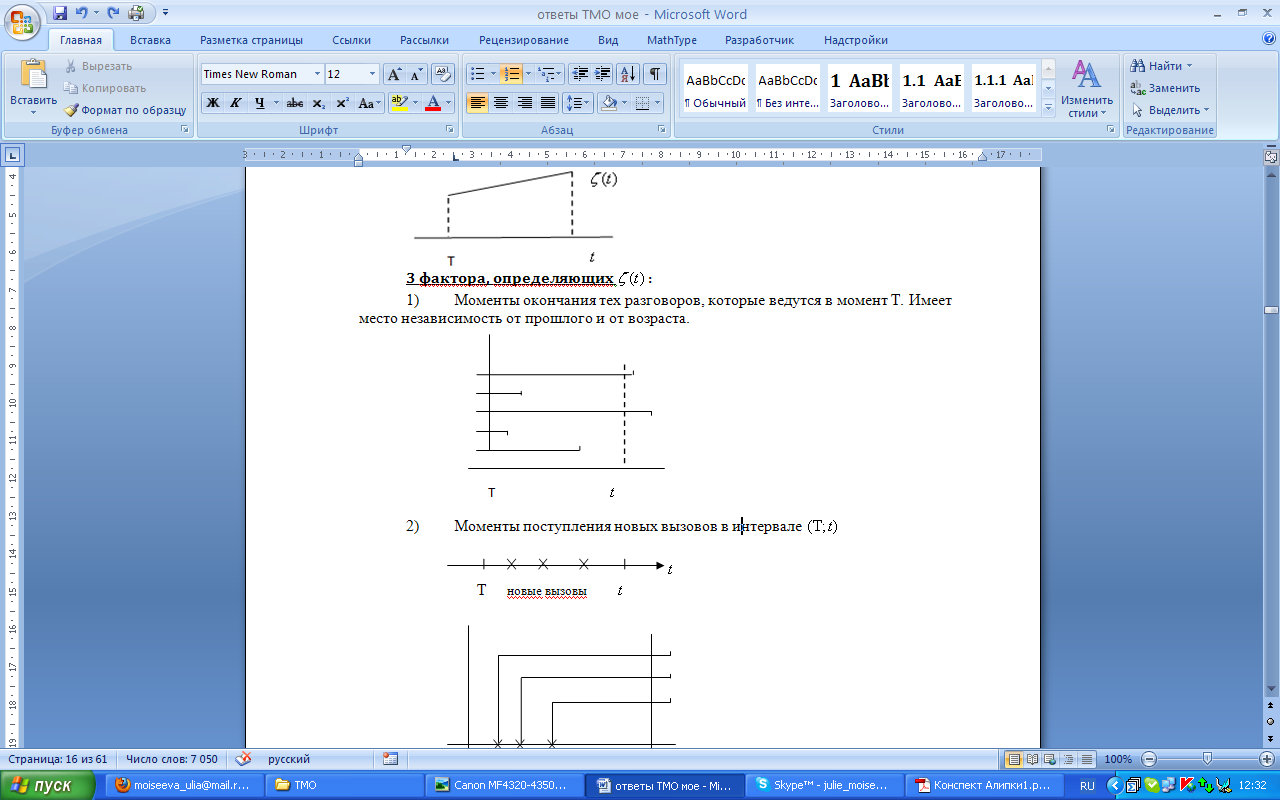
Моменты поступления новых вызовов в интервале
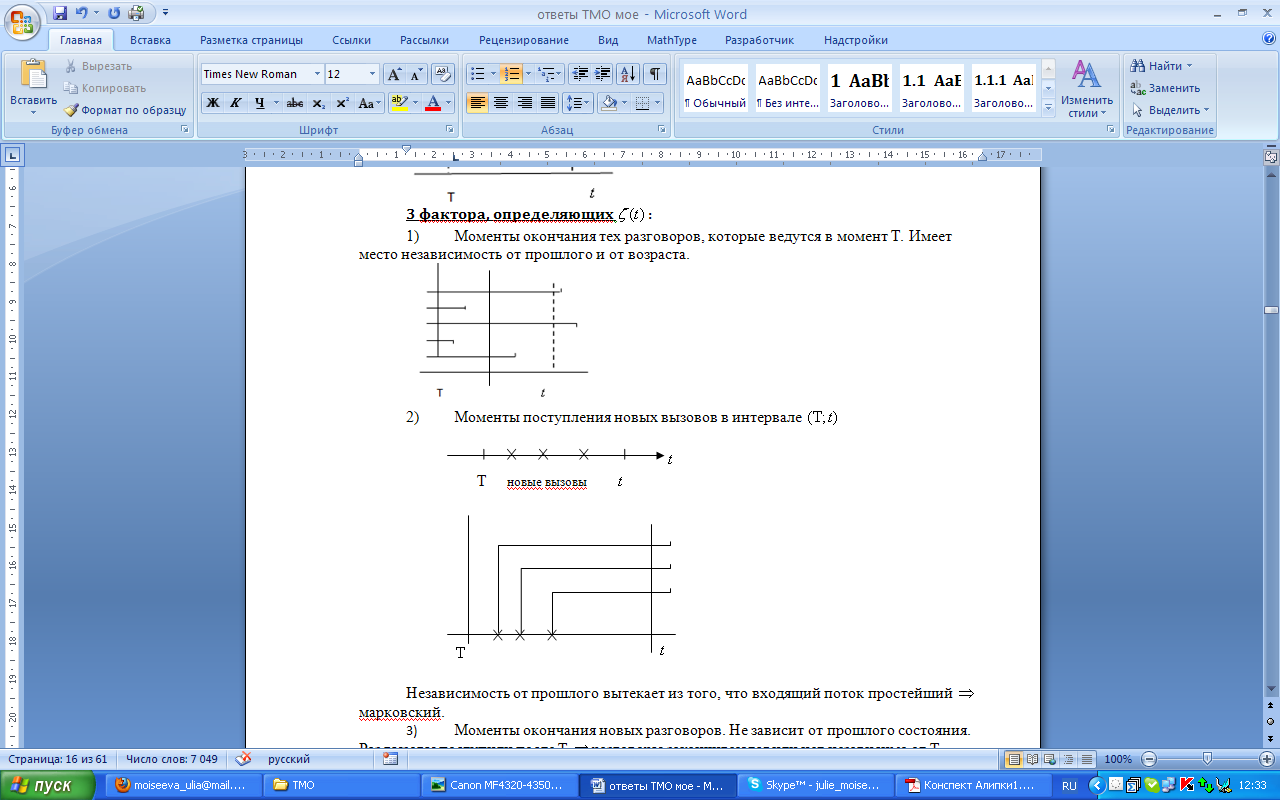
Независимость от прошлого вытекает из того, что входящий поток простейший марковский.
Моменты окончания новых разговоров. Не зависит от прошлого состояния. Раз вызовы поступили после T разговоры заканчиваются или нет независимо от T.
9.Выходящий поток из непрерывно загруженной со
Частный случай n=1. Пусть имеется очередь вызовов достаточной длины. Как только линия освобождается, в очереди есть вызов, который занимает сразу эту освобожденную линию, т.о. СО загружена непрерывно.
Доказательство:
-Рассмотренный поток освобождений линии является марковским, так как количество освобождений в промежутке не зависит от количества освобождений до этого промежутка.
-
,
длины разговоров независимы друг от
друга, все 
распределены по показательному закону
и тоже независимы (т.к. длины независимы),
следовательно, получаем простейший
поток с параметром β. Ч.т.д.
-вероятность
k освобождений за промежуток длины t.
Пример:
Пусть
– время исправной работы прибора.
распределено по показательному закону
с параметром β. После поломки прибор
заменяется на новый (такой же).
-вероятность,
что за время t произойдет ровно k поломок.
-
?
Физически линии нет, условная линия – место, занимаемое прибором. Линия занята-прибор исправен.
n=1, = длина разговора = время исправ. работы.
Общий случай. n линий
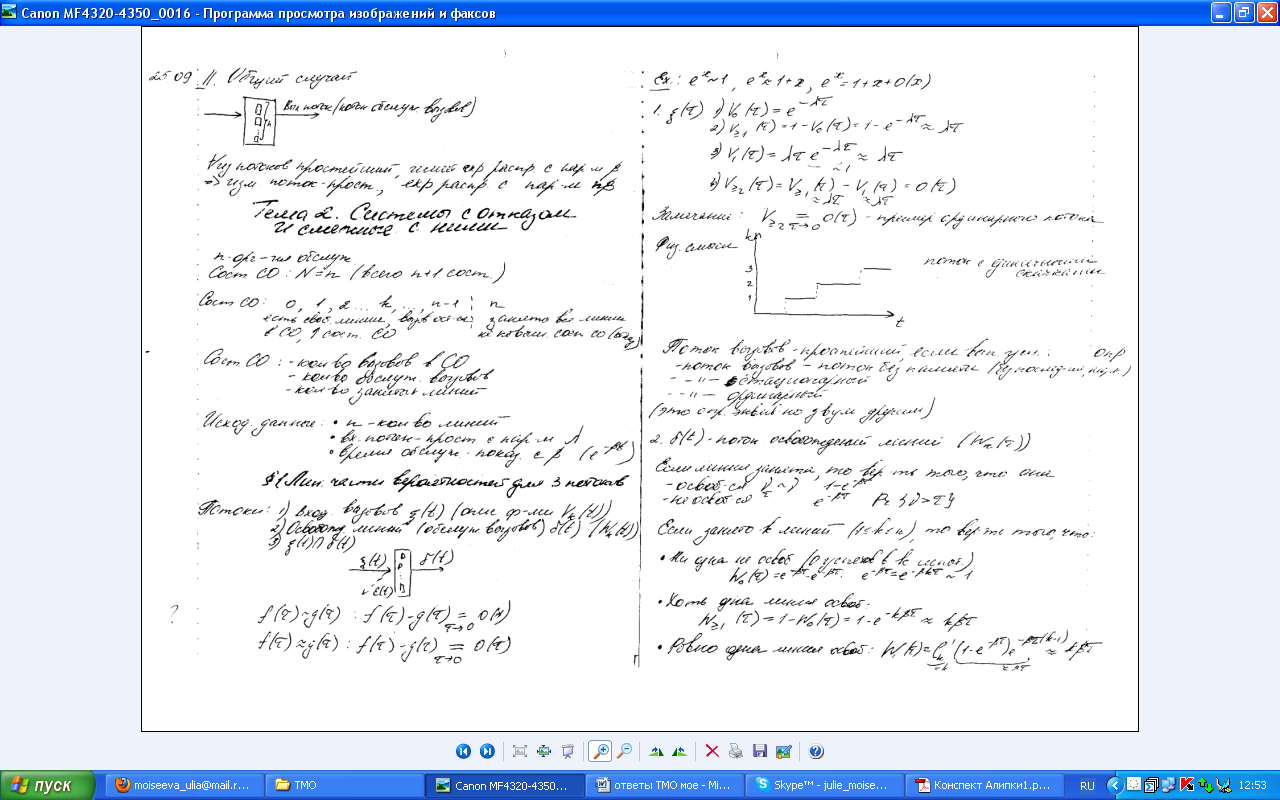
Любой из потоков—простейший, имеет показательное распределение с параметром β , следовательно, выходящий поток – простейший поток, распределен показательно с параметром nβ.
