Допущения в тмо:
Кажд. вызов обслуж-ся только одной линией (индивидуальное обслуж-е).
Кажд. линия в любой данный момент обслуживает не более одного вызова
Любой начатый разговор не прерывается вплоть до его завершения
Длины разговоров (работа линий) не зависят от вход. потока и друг от др.
СО, где допускаются очереди (СОЖ или смешанные), предполагает обслуживание в порядке очереди - т.о., нет приоритетных вызовов.
4. Понятие о пгр, стационарное решение и его интерпретация Определение.
- дискретный случайный
процесс (с.п.) (
).
Пусть T – произвольный
момент времени;
Пусть
;
.
За время
(
)
процесс переходит в состояние:
а)
с
вероятностью
(
)
б)
с вероятностью
(
)
в)
с вероятностью
Если для с.п. выполн. эти усл., он наз. ПГР (процесс гибели и размножения).
- параметры процесса,
не зависящие от времени, от прошлых
состояний системы.
Вероятность перехода
за
равна
,
если
.
- значит, что численность
популяции в момент
равна
.
,
(гибель)
и
(размножение)– три существенных (наиб.
вероят.) сост. при переходе из
в
.
для любого ПГР равно
0.
Если
(частный случай), это процесс (чистого)
размножения (ПР).
Е
сли
,
то
(т.е. невозможно
).
Частный случай: когда
при этом ещё и
.
Крайний частный случай:
Если
,
либо
(для
случая
)
– это процесс гибели (ПГ).
Первонач. задачи ТМО были решены для пересечения множества Марковских с.п. и множества ПГР.
Постановка задачи Эрланга для пгг
- ПГР.
- вер-ть того, что в мом.
в СО
выз.
Нахождение мн-ва ф-ций
- задача Эрланга
Свойства :
Неотрицательность:
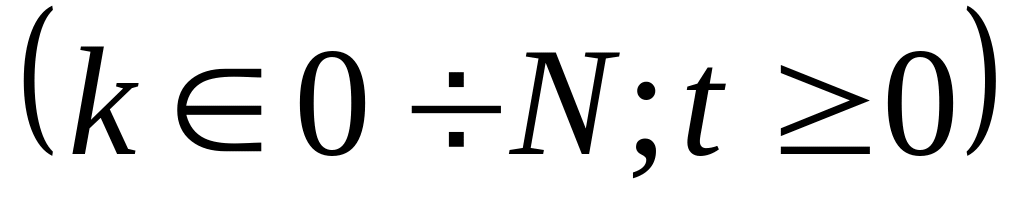;Нормировочное условие:
.
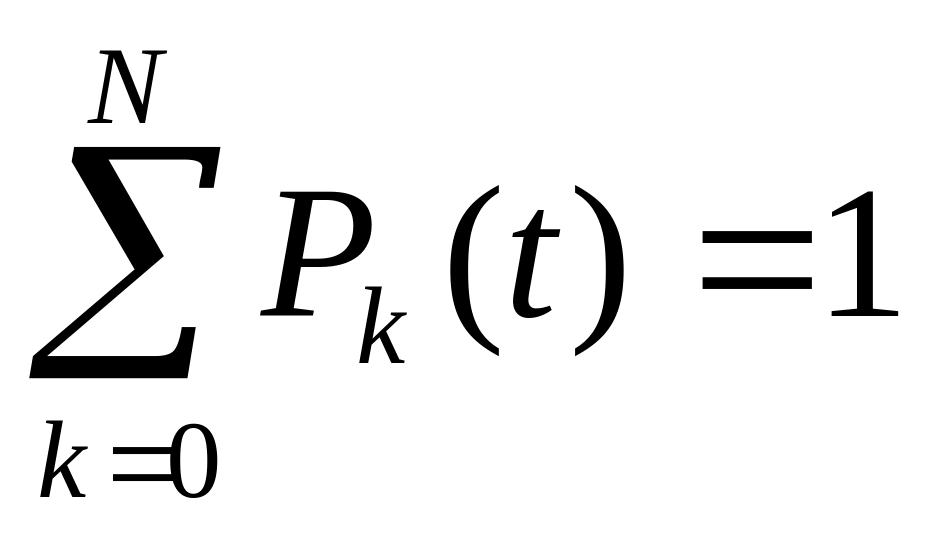
Если
,
- взрыв (бесконеч. сост-е) невозмож.
Пусть
.
- начальные вероятности
(исходные данные, известны).
Требуется найти: закон распр-я вер-тей на любой последующий момент времени.
Каждая
зависит от
;
1.
;
;
при некоторых условиях;
2.
не зависит от
(
).
Нахождение
(
)
- задача Эрланга
в предельной форме
- задача
нахождения стационарного решения.
Свойства
:
1. Неотрицательность: ;
2. Нормировочные условия:
Можно показать, что
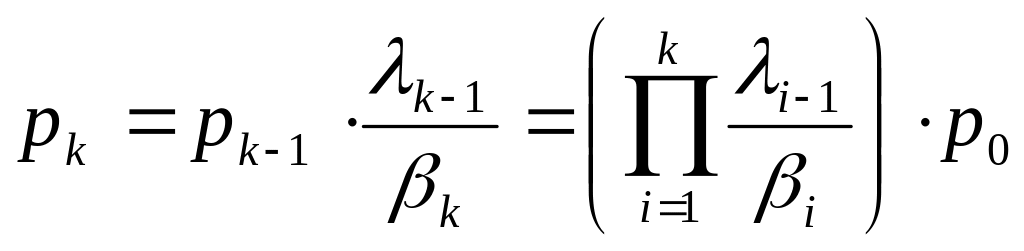(без док-ва).
- ?
.
Пусть правое слагаемое меньше
,
если
//при
тоже//. Тогда
След.
(
).
Интерпретация :
- вероятность
-го
состояния,
(ровно
вызовов в системе).
Пусть
- время пребывания СО
в состоянии
.
- среднее относительное
время пребывания СО в состоянии
(доля времени, в течение которого в СО
вызовов).
Теорема (эргодическая):
,
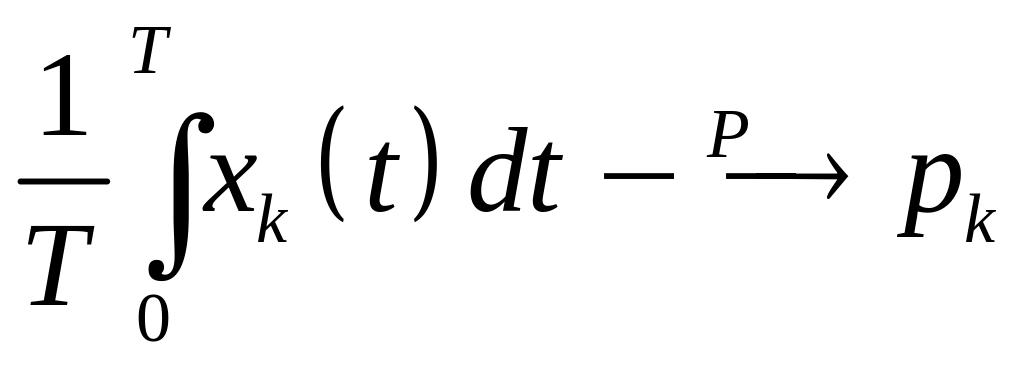то есть
- среднее относительное
время пребывания процесса в состоянии
.
Если
- большое, то
- средняя длина промежутка времени, в
течение которого в системе было ровно
вызовов.
5.Задание потока вызовов
Существует 2 способа задания потока вызовов:
Случайный процесс;
Последовательность случайных величин.
Способ 1:
Поток вызовов как случайный процесс.
- произвольный момент
времени;
.
- число вызовов,
поступивших в промежутке
.
Если меняется, то - семейство случайных величин, зависящих от - случайный процесс.
Свойства :
Дискретность:
Монотонность реализации: количество вызовов не уменьшается с течением времени. Всякая - неубывающая функция.
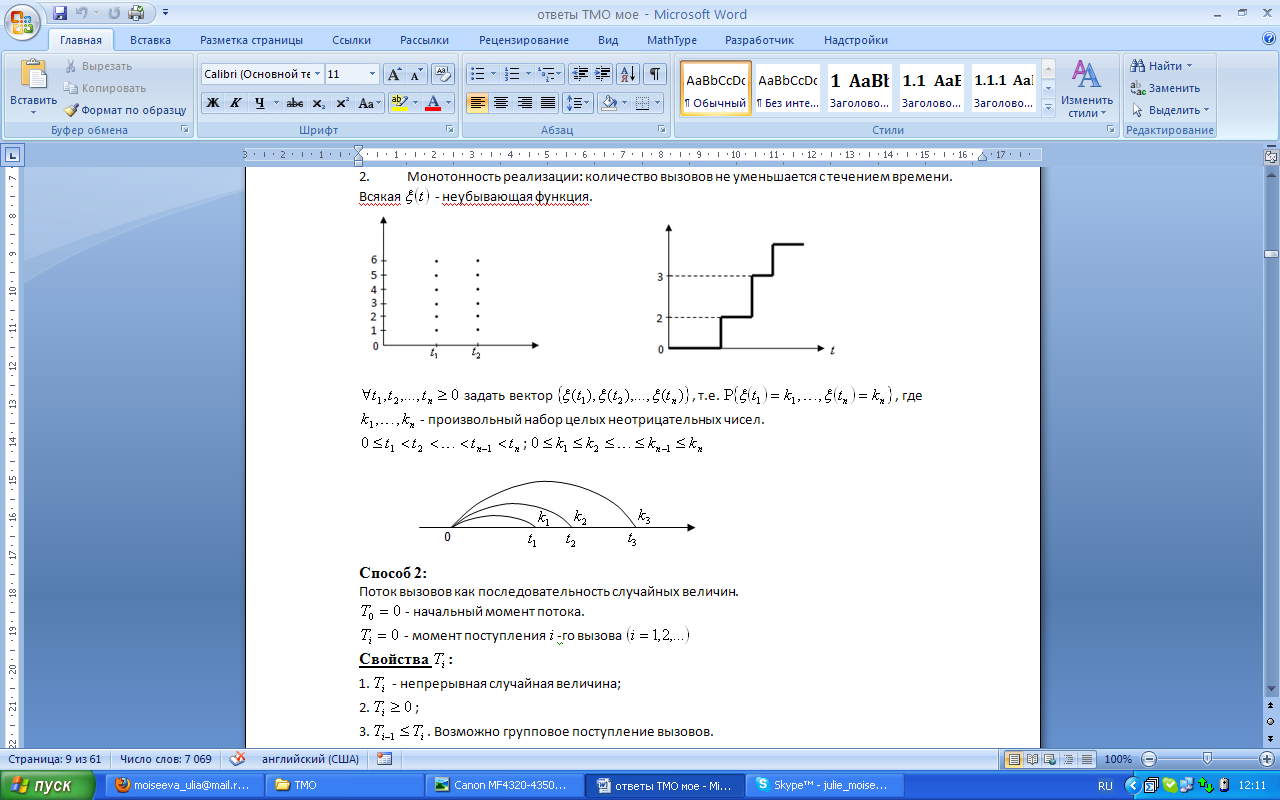
задать вектор
,
т.е.
,
где
- произвольный набор целых неотрицательных
чисел.
;
Способ 2:
Поток вызовов как последовательность случайных величин.
- начальный момент
потока.
- момент поступления
-го
вызова
Свойства
:
1. - непрерывная случайная величина;
2.
;
3.
.
Возможно групповое поступление вызовов.
Пусть
, где i>1, тогда
- длина промежутка времени между моментами
поступления i-1
и i
вызова.
– от начального момента потока до
поступления первого вызова.
Свойства
:
- непрерывная случайная величина;
;
Поток
вызовов –
последовательность моментов их
поступления 
,
образованных длинами промежутков
- n-мерный случайный
вектор.
Поток задан, если известна функция распределения такого вектора:
Оба способа задания потока равносильны.