2. Закон Пуассона

: 0,1,2...,k,…

Сл. по - дискр с.в.

, k=0,1,2,…

0<a< , a – параметр

.

2. Биномиальный закон

n – независимых испытаний с двумя исходами в каждом испытании

p – вероятность успеха

- количество успехов в серии из n испытаний

.

Понятие о случайном процессе и его задании

t - вещественное неопр. Число

x(t)

Если t – фиксир, то x(t) –с.в., если t меняется, то x(t) – c.п. (с.ф.)

С.п. x(t) - (n=1,2,..)

Известен закон распределения

(1)

Дискретная с.п.

В ТМО x(t):0,1,2,3,..i,…,N, (

x(t) – дискр с.п.

Пример: 1. – количество вызовов, поступивших в СО в промежуток времени (0,t).

:0,1,2,..,N,..

N=

i вызов

S(t) – монотонно неубыв. функция

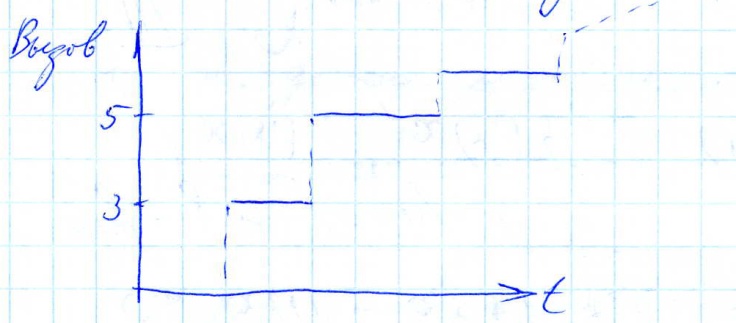Реализация случайного процесса

2. - состояние (число вызовов) в СО на t.

: 0,1,2,3,..i,…,N, (

- вероятность того, что в момент t в СО находится i вызовов.

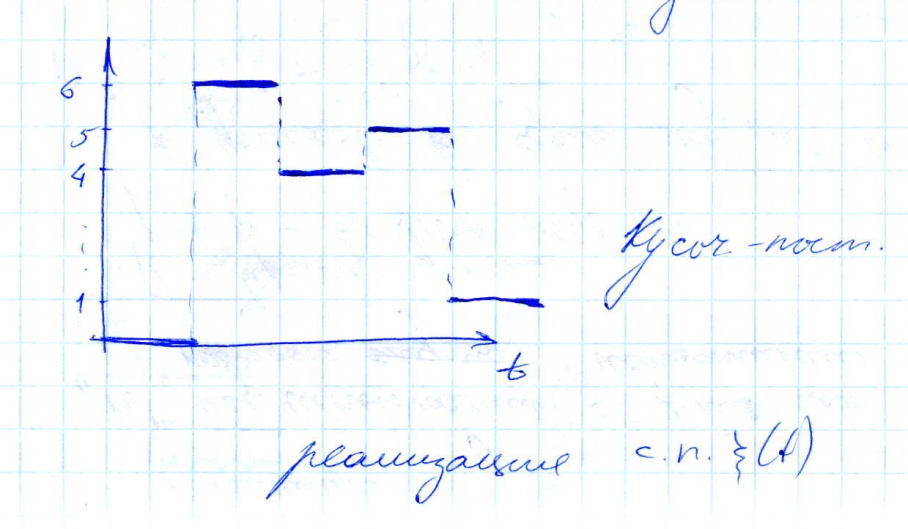Реализация с.п.

x(t)- дискр. с.п.

x(t):0,1,2,3,..i,…,N, (

вектор (1)

(n=1,2,..)

, -функция распределения вектора (1)

Марковские с.п.

x(t) – дискр с.п., x(t):0,1,2,…,N

T – любой момент времени,

,

.

Марковский с.п. – с.п. x(t): вероятность перехода из состояния i в состояние k за не зависит от прошлого течения процесса, т.е. от сотояния до T. Будущее не зависит от прошлого, а только от настоящего.

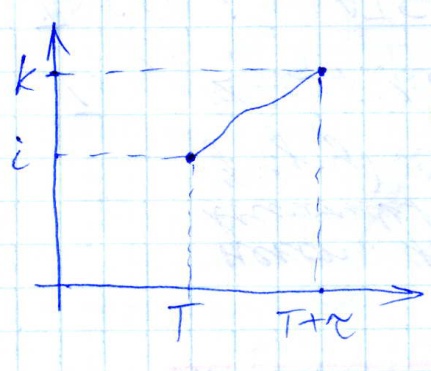
Переходная вероятность: ,

3.Основные понятия и допущения в тмо

Система массового обслуживания (СО) – организация, которая может выполнять работу (предоставлять услугу) одного вида. Пр.: АТС, магазин, порт, аэродром.

Вызов (требование) – заявка на выполнение работы (предоставление услуги), на которую способна данная система.

Входящий поток вызовов - вызовы, поступающие в данную СО и нуждающиеся в услуге, на которую способна данная СО.

Пр. вход. потока : поток вызовов на АТС, поток судов, поток сломанных объектов.

Для СО с ожиданием (СОЖ) входящий поток распадается на поток немедленно обслуживаемых вызовов и поток вызовов, попадающих в очередь.

Выходящий поток – вызовы, покидающие данную СО. Для систем, где существуют отказы, он распадается на поток обслуженных вызовов и поток отказов.

С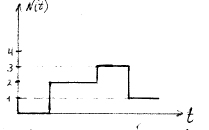 остояние СО – количество вызовов, имеющихся в СО на тот или иной момент времени , принимает значения ( ).

// У Алипова - так на картинке. У нас это //

1. Состояния СО по : - случ. процесс (с.п.);

2. Состояние в стационарном решении: - случайная величина (с.в.), .

Линия – некий объект (прибор), предназначенный для обслуживания. Иногда реальных линий может и не быть, и их можно ввести идеально. Пр. линий: продавец, парикмахер, причал (док), почтальон.

Пучок линий – совокупность всех линий в СО. Он конечный, если ( - количество линий в пучке), бесконечный – в противном случае.

Пучок линий полнодоступный, если любая его линия может обслуживать любой поступающий вызов, и любой поступающий вызов согласен быть обслуженным любой линией (все линии взаимозаменяемые).

Пучок линий упорядоченный, если все линии пронумерованы, и вызов занимает линию с наименьшим номером из числа свободных линий.

Разговор (длина разговора) - - время обслуживания на любой линии. - непрер. случайная величина, , функция распределения считается известной.

Функция распределения: , , .

- известна. Свойства :

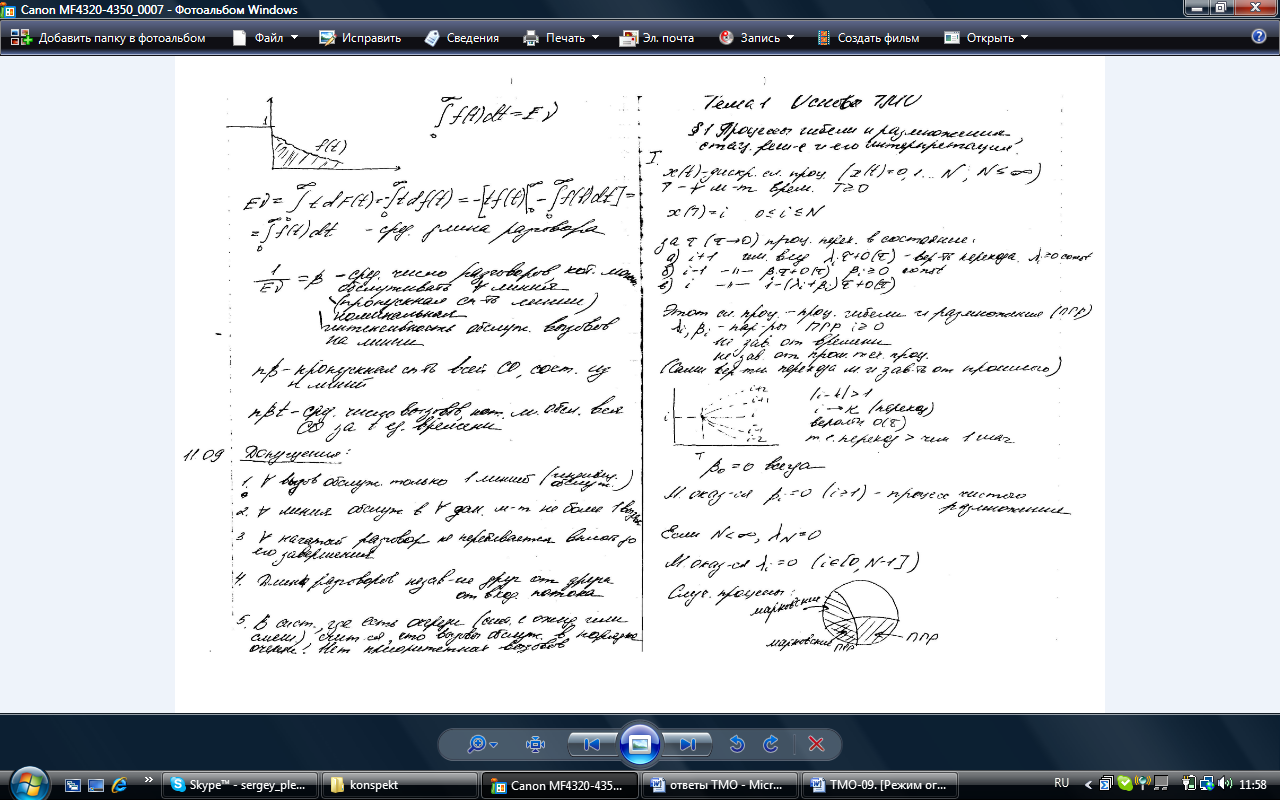1. не возрастает

2. 

3. 

4. ~

5. .

- средняя длина разговора

- интенсивность обслуж-я вызовов на линии - пропускная спос-ть линии (номинальная) - сред. число выз., кот. мож. обслуж. кажд. линия за ед. вр..

- пропускная способность СО.

- пропускная способность за единиц времени.