1.О задачах тмо

ТМО – один из разделов теории вероятностей в области её практического применения. По сути – это теория очередей. Название ТМО дал академик Хинчин.

Эрланг – основоположник теории. Свой вклад в становление ТМО сделали Пальм (шведский математик), Хинчин, Марков, Колмогоров.

Первоначально в качестве системы обслуживания (СО) рассматривалась АТС.

Количество линий связи конечно. Количество вызовов и длины разговоров – случайные величины.

Если свободная линия, то поступивший вызов ее занимает. Если в момент поступления вызова все линии заняты, то его дальнейшая «участь» зависит от типа СО.

Типы СО:

СО с отказом (потерей)
СО с ожиданием
Смешанные СО (пример: системы с ограниченной очередью (числом мест ожидания), m – максимально допустимый размер очереди. Вызов ставится в очередь, если длина очереди меньше m, получает отказ, если равно m).
Бесконечный пучок ( n=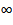, нет ни отказов, ни ожиданий, возможно в теории)

Основные задачи ТМО:

Нахождение стационарного решения - вероятностей отдельных состояний СО в установившемся режиме независимо от времени.

Состояние СО на момент времени t: .

-количество вызовов в СО на момент t

- случайный процесс.

- случайная величина, стационарный процесс.

Нахождение показателей эффективности функционирования данной СО.

Показатели: -абсолютные

-относительные (Коэффициенты-средняя доля абсолютного показателя, коэффициент обслуживания, коэффициент занятого времени.)

Для СО с отказом основным показателем является (вероятность отказа, вероятность застать все линии занятыми).

Для СО с ожиданием - - время ожидания (непрыревная, ) (ищем функцию распределения ). Показатель эффективности - среднее время ожидания. Для дискретной случайной величины (длины очереди) - средняя длина очереди.

Для смешанных СО - , , .

В СО, где допускаются очереди, ищут условия, при которых очередь ведет себя естественным образом (не растет до бесконечности), т.е. СО справляется с обслуживанием.
Расчет рационального числа линий (n) в данной СО. 2 точки зрения:

а) С точки зрения вызовов, так как _, чем больше число линий, тем лучше.

б) с т. зрения самой СО n не должно быть чрезмерно большим (иначе будут простои+неэффективная работа) необходим поиск «золотой середины», чтобы показатели эфф-ти СО были наилучшими.