80. Конические зубчатые передачи. Геометрические параметры. Силы в зацеплении. Расчет зубьев прямозубых конических передач.
Конические
передачи
являются передачами с пересекающимися
осями вращения звеньев. Применяются,
главным образом, передачи с углом между
осями
.
Передаточное отношение равно:
(2.3.44)
.
ок
2.3.18 Геометрия конического колеса
Достоинства: возможность передачи вращающегося момента под углом.
Недостатки: сложная технология изготовления и монтажа передач.
Основные геометрические размеры определяют в зависимости от модуля и числа зубьев. Высота и толщина зубьев конических колёс постепенно уменьшается по мере приближения к вершине конуса. Соответственно изменяются шаг, модуль и делительные диаметры, которых может быть бесчисленное множество. Основные геометрические размеры имеют обозначения, принятые для прямозубых конических передач.
Внешний
диаметр
:
где
-
максимальный модуль зубьев – внешний
окружной модуль, полученный по внешнему
торцу колеса. Внешнее конусное расстояние
Среднее
конусное расстояние
,
где
b –
ширина зубчатого венца колеса
-
коэффициент ширины зубчатого венца
относительно внешнего конусного
расстояния.
-
углы делительных конусов;
Средний
модуль
Средние делительные диаметры:
В
соответствии с исходным контуром
прямозубых конических колёс радиальный
зазор c=0,2
, тогда внешняя высота головки зуба
и
внешняя высота ножки зуба
.
Внешние диаметры вершин зубьев
Угол
ножки зуба
Угол головки зуба
;
Силы
в зацеплении
определяют по размерам в среднем сечении
зуба шестерни. На шестерню конической
прямозубой передачи действуют три силы
рис.2.3.19:
окружная
,
радиальная
,
осевая
.
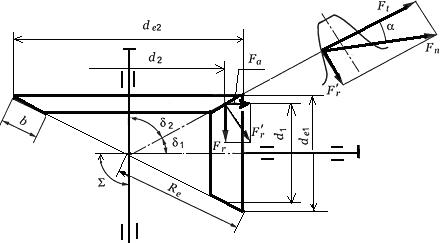Рисунок
2.3.19 Схема действия сил в зацеплении
конических колес
Для
колеса направление сил противоположно,
при этом:
;
;
Направление
окружных сил F, как и в цилиндрической
передаче зависит от направления вращения
колёс. Осевые силы
всегда
направлены от вершин конусов, радиальные
-
к осям вращения колёс. Конические
передачи с круговыми зубьями получили
преимущественное применение. По сравнению
с коническими прямозубыми они менее
чувствительны к нарушению точности
взаимного расположения колёс, их
изготовление проще. Недостаток передач
с круговыми зубьями – изменение величины
и знака осевых сил при реверсе. Ось
кругового зуба – это дуга окружности
соответствующего диаметра резцовой
головки. Нарезание зубьев резцовой
головки обеспечивает высокую
производительность и низкую стоимость
колёс. Угол наклона кругового зуба
переменный. За расчётный принимают угол
на окружности среднего диаметра колеса,
обычно Значение выбирают исходя из
обеспечения плавности зацепления.
Расчет на контактную прочность. Прочностной расчет конической передачи основан на допущении, что несущая способность зубьев конического колеса такая же как у эквивалентного цилиндрического. Эквивалентным колесом называется такое цилиндрическое колесо, у которого делительный диаметр и модуль равны делительному диаметру и модулю в среднем нормальном сечении реального конического колеса.
Межосевое расстояние эквивалентной передачи
Передаточное число эквивалентной передачи
Момент на эквивалентном колесе
Расчет конических зубчатых передач на изгиб. Формула проверочного расчёта конических прямозубых передач:
Формула проектировочного расчёта конических прямозубых передач:
Условие прочности
где
-
коэффициент вида конических колёс. Для
прямозубых колёс
;
для колёс с круговыми зубьями
;
и
-
внешний и окружёной модули; YF – коэффициент
формы зуба. Внешний окружной модуль
или
определяют
расчётом на изгиб по формуле
Минимальное число зубьев шестерни z конической передачи с круговыми зубьями определяют по формуле
