75. Зубчатые передачи. Расчетная нагрузка. Коэффициент нагрузки.

Зубчатая передача – это высшая кинематическая пара, в которой вращение ведущего звена передается ведомому зубчатому колесу.

За расчетную нагрузку принимают максимальное значение удельной нагрузки, распределенной по линии контакта зубьев:

где Fn — нормальная сила в зацеплении;

K=K^K ν — коэффициент расчетной нагрузки;

К — коэффициент концентрации нагрузки;

Κν — коэффициент динамической нагрузки;

LΣ — суммарная длина линии контакта зубьев.

Коэффициент концентрации нагрузки Концентрация или неравномерность распределения нагрузки по длине зуба связана с деформацией валов, корпусов, опор и самих зубчатых колес, а также с погрешностями изготовления передачи.

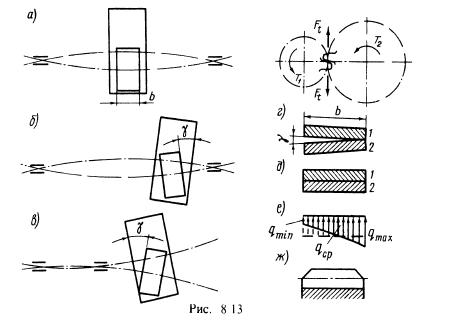  На рис. 8.13 изображено взаимное расположение зубчатых колес при деформированных валах в случаях: симметричного (рис. 8.13, а), несимметричного (рис. 8.13, б) и консольного (рис. 8.13, в) расположения колес относительно опор. Валы прогибаются в противоположные стороны под действием сил в зацеплении.

При симметричном расположении опор прогиб валов не вызывает перекоса зубчатых колес и, следовательно, почти не нарушает распределения нагрузки по длине зуба. Это самый благоприятный случай. При несимметричном и консольном расположении опор колеса перекашиваются на угол у, что приводит к нарушению правильного касания зубьев. Если бы зубья были абсолютно жесткими, то они соприкасались бы только своими концами (см. рис. 8.13, г, на котором изображено сечение зубьев плоскостью зацепления). Деформация зубьев уменьшает влияние перекосов и в большинстве случаев сохраняет их соприкасание по всей длине (рис. 8.13, д). Однако при этом нагрузка перераспределяется в соответствии с деформацией отдельных участков зубьев (рис. 8.13, е). Отношение где q_ср— средняя интенсивность нагрузки. Концентрация нагрузки увеличивает контактные напряжения и напряжения изгиба. Для уменьшения опасности выламывания углов зубьев на практике применяют колеса со срезанными углами (см. рис. 8.13, ж).

76. Расчет прямозубых цилиндрических передач на прочность по контактным напряжениям. Силы в зацеплении.

Расчёт производят при контакте зубьев в полюсе зацепления П. Контакт зубьев рассматривают как контакт двух цилиндров с радиусом р₁ и р₂. При этом наибольшие контактные напряжения определяют по формуле Герца:

Расчет по контактной прочности сводится к проверке условия . После преобразования формулы Герца для контакта цилиндрических поверхностей получают формулу для определения межосевого расстояния

где Т₂ – вращающий момент на тихоходном валу, Н м; u - передаточное число; К_a = 49,5 МПа – для прямозубых колес; 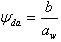- коэффициент ширины колеса по межцентровому расстоянию, его можно определить по формуле где - выбирается из справочных таблиц, - допускаемое контактное напряжение, где - коэффициент долговечности, -предел контактной выносливости, определяется для заданного материала из таблиц, = 1,1- 1,3 - допускаемый коэффициент запаса прочности, - базовое число циклов нагружения, - расчетное число циклов нагружения, Lh – полный ресурс в час. Определив геометрические размеры передачи, ее проверяют на контактную прочность по формуле:

где - коэффициент нагрузки при расчете по контактным напряжениям, - коэффициент нагрузки, учитывающий распределение нагрузки между зубьями (для прямозубых передач =1), - коэффициент нагрузки, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца (по длине контактных линий), =1,25 - коэффициент нагрузки, учитывающий дополнительные динамические нагрузки.

Силы в зацеплении определяют в полюсе зацепления. На шестерню действует вращательный момент, который создаёт распределённую по контактным линиям зуба колеса нагрузку. Эту нагрузку заменяют равнодействующей силой , направленной по линии зацепления nn и приложенной в полюсе. Силами трения в зацеплении пренебрегают, так как они малы. Силу раскладывают на окружную Ft и радиальную Fr (рис. 2.3.12):

; Рисунок 2.3.12 Схема действия сил в зубчатом зацеплении

Такое разложение силы на составляющие удобно для расчёта зубьев и валов. На ведомом колесе направление силы F_t совпадает с направлением вращения, а на ведущем – противоположно ему, т.е. силы на ведущем и ведомом колёсах всегда направлены против действия соответствующих моментов. Радиальные силы F_r направлены к осям вращения колёс и создают «распор» в передаче. Расчет на прочность зубчатых колес проводят по двум условиям прочности: по контактным напряжениям и по напряжениям изгиба. При расчете по контактным напряжениям для всех коэффициентов применяется индекс «Н», по напряжениям изгиба – индекс «F».