2. Метод дискретных ординат.

Билет 7.

1. Моделирование траекторий нейтронов и фотонов: определение длины свободного пробега.

Длина свободного пробега L. Плотность распределения случайной величины L определяется транспортным ядром интегрального уравнения переноса. Опуская для простоты энергетическую переменную:

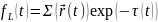
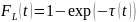t>0

1. Гомогенная среда. , , ,

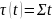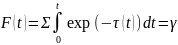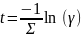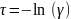
2 . Гетерогенная среда.

Алгоритм определения Длины свободного пробега.

Метод дельта-рассеяния.

Σ_m- максимальное сечение, которое может иметь в место при движении частицы от точки в направлении .

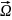Генерируем две последовательности независимых значений: первая t₁,t₂,…,t_n с плотностью распределения 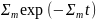и вторая 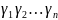с равномерной плотностью распределения 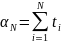. Пусть

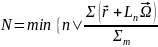тогда .

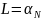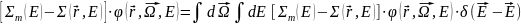
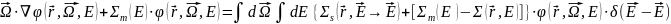
2. Многогрупповое приближение уравнения переноса.

Билет 8.

1. Моделирование траекторий нейтронов и фотонов: определение параметров частиц после столкновения.

Эти параметры включают энергию и направление движения рассеянной первичной частицы, а так же тип, число, энергию и направление движения любых вторичных частиц, родившихся при взаимодействии.

Рассмотрим выбор энергии и направления движения фотона после комптоновского рассеяния. Плотность распределения энергии после рассеяния пропорциональна функции

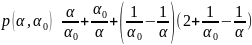при

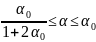
Алгоритм определения 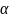: 1) выбираем пару случайных чисел . 2)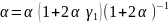

3) если 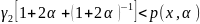то выбираем , иначе снова выполняться 1).

Азимутальный угол рассеяния 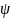выбирается из равномерного распределения, а косинус полярного угла 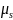рассчитывается по формуле 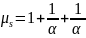или по формуле Карлсона:

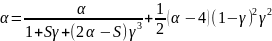, где

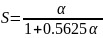
Рассмотрим упругое рассеяние нейтронов.

Для водорода угловое рассеяние изотропно в системе центра инерции, откуда и

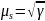
В общем случае упругое рассеяние анизатропно. Плотность распределения косинуса угла рассеяния обычно задаётся в разложения в ряд по полиномам Лежандра.

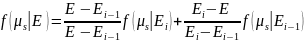
Выбираем , если 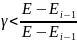, то моделируется соответственно плотности 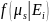, в противном случае – соответственно .

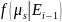2. Сопряженное уравнение переноса и физический смысл его решения.

Билет 9.

1. Моделирование траекторий нейтронов и фотонов: геометрическое построение траекторий.

Геометрическое построение траектории в исследуемой композиции осуществляется геометрическим блоком или модулем. Задачей блока является ответ на 2 вопроса: 1. В какой зоне, материале происходит каждое столкновение? 2. Каково оптическое расстояние между точкой столкновения и точкой детектирования? При моделировании переноса излучения в однородных средах алгоритм геометрического модуля очень прост. На входе в модуль задаются: координаты n-ого рассеяния, направление движения и длина пробега до (n+1)-взаимодействия. Координаты (n+1)-взаимодействия определяются по формулам (в декартовой системе координат):

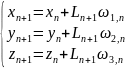
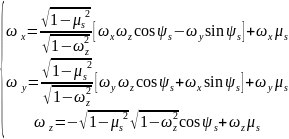
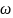- после рассеяния, 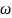– до рассеяния.