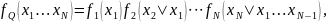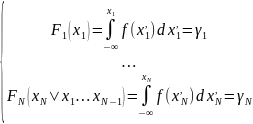Билет 1.

1. Случайные величины и их функции распределения. Свойства выборки из плотности распределения.

Событие – тот или иной исход события. Событие, включающее все возможные исходы эксперимента, называется достоверным и обозначается Ω. Вероятность определяется как вещественная функция на множестве событий, удовлетворяющее условиям: 1) р(ø)=0, р(Ω)=1, 0≤р(ω)≤1 для любого ω; 2) 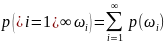, если 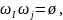i≠j, где ω – событие, ø – невозможное событие.

λ(t)={ ω : ξ(ω)≤t} – некоторое подмножество событий ω, для которых ξ(ω)≤t. ξ – случайная величина на Ω. р(ξ<t)=p(ω: ξ(ω)<t) – функция распределения случайной величины =F(t). Её свойства:

1)

2) F(t) – монотонно неубывающая функция.

3) р(а< ξ≤b )=F(b)-F(a)

4) f(t) – плотность распределения. 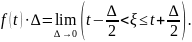при наличии производной F(t) в точка t.

M ξ=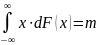 – матожидание.

D ξ=M(ξ-m)²=σ² – дисперсия.

2. Метод сферических гармоник.

Билет 2.

1. Получение случайных чисел с заданным распределением: метод обратных функций, метод исключения.

ξ - случайная величина, f(t) - плотность распределения. t₁, t₂... t_N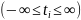 – выборка, случайная величина ξ в N экспериментах. Условия:

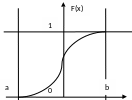
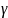– случайная величина, равномерно распределённая на [0,1]. f(t)=1, при 0≤γ≤1.

Метод обратных функций.

ξ - случайная величина на a≤x≤b и f(x)>0.Покажем, что выборочное значение t случайной величины можно выбрать из уравнения 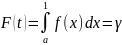или .

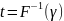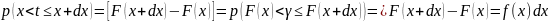
На каком то участке может быть, что f(x) || ОХ, тогда t=sup(x) F(x)<γ.

Метод исключения.

Данный метод свободен от недостатков метода обратных функций, связанных с получением аналитического решения. ξ - случайная величина на a≤x≤b и f(x)>0.

М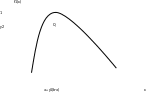 =supf(x) f₁(x)=f(x)/M . Используя пару равномерно распределённых на [0,1] случайных чисел (γ₁ γ₂), найдём координаты случайной точки Q={a+ γ₁(b-a), γ₂}. Если эта точка окажется под кривой f₁(x),то t= a+ γ₁(b-a) принимается в качестве случайной величины ξ с плотностью распределения f(x). В противном случае выбирается другая пара чисел и всё повторяется.

,

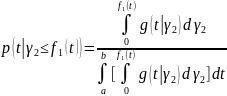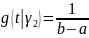
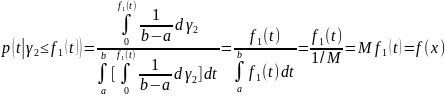
ε - эффективность метода. ε=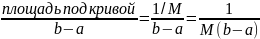

2. P1-приближение метода сферических гармоник.

Билет 3.

1. Получение случайных чисел с заданным распределением: метод равновероятных интервалов, метод суперпозиции, моделирование многомерных случайных событий.

Метод равновероятных интервалов (таблицы) основан на замене моделируемой случайной величины ξ дискретной величиной η, принимающей с равной вероятностью значения х_i (i=1..N). f(x), a≤x≤b.

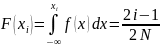. Ступенчатая аппроксимация функции распределения.

Метод суперпозиции. ξ, a≤x≤b 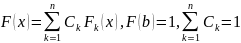. Вводим случайную дискретную величину η принимающую значение k с вероятность С_k. Берём случайные числа (γ₁ γ₂),и по γ₁ разыгрываем значение η=k, а затем решаем уравнение 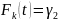. T будет представлять выборочное значение случайной величины ξ. .

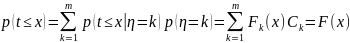Моделирование многомерных случайных событий. Если в одном эксперименте наблюдается несколько случайных величин, то разыгрывание их значений можно рассматривать как моделирование координат n-мерной случайной величин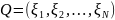ы .Все случайные величины независимы:

Зависимые случайные величины: :