Задача . Найти двухопорную балку оа длиной l действует сосредоточенная сила р, приложенная к точке в на расстояниях l1 и l2 от концов. Найти уравнение линии и определить прогиб h в точке в.

откуда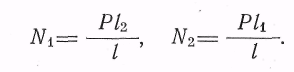

▲Составим уравнение для изгибающего момента.

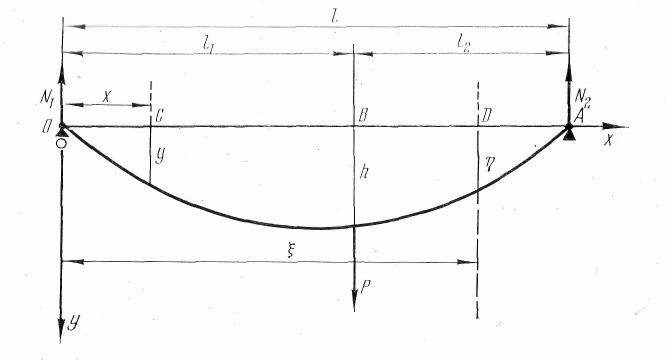
Рис. 68 В любом сечении С(х, у) части ОБ балки (рис. 68) получим

или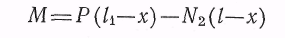

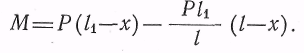(О В любом сечении D(Ј, щ) части В А балки имеем:

(2)

Моменты (1) и (2) подставим в дифференциальное уравнение упругой линии и получим два разных дифференциальных уравнения соответственно для частей ОБ и ВА балки:

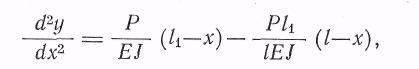
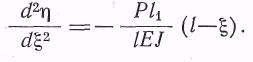
Решая оба эти уравнения типа y"=f(x), получим для левой части балки: первый интеграл

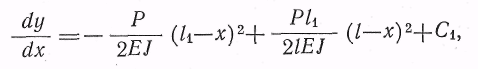
второй интеграл, т. е. общее решение,

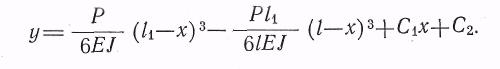
Для правой части балки: первый интеграл

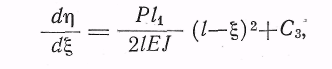
второй интеграл, т. е. общее решение,

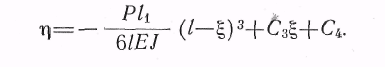
Начальные условия на опорах О и Л:

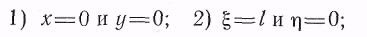
в точке В приложения силы Р:

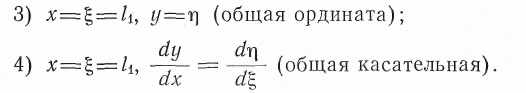
Подставив начальные условия в первые и вторые интегралы, найдем:

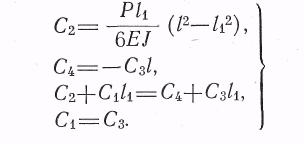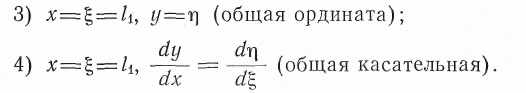
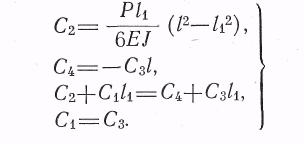(5) Решаем систему (5):

»