Пример 6. Найти силу тяги состава с рудой по истечении времени t имеющего начальную скорость v₀, двигающегося с ускорением прямопропорциональным силе тяги F=b-kv и обратно пропорциональным массе состава с рудой. Если в начальный момент времени при t =0 сила тяги определяется выражением F(t)= F₀=b-kv₀.

▲ скорость движения состава с рудой является функцией времени, т.е. v= v(t), а его ускорение определяется 2-м законом Ньютона

, где F=b-kv.

Поэтому дифференциальное уравнение исходной задачи будет иметь вид:

. ()

Разделяя переменные в этом уравнении, получим уравнение с разделенными переменными

,

Интегрируя которое, найдем общее решение уравнения ()

или ()

В решении () удовлетворим начальному условию – v(0)=v₀.

.

Подставив найденное значение постоянной С в общее решение (), получим решение задачи Коши:

или

.

Таким образом, искомую силу тяги состава с рудой в любой момент времени, найдем из последнего равенства, избавившись в нем от логарифма

.▲

Пример . Трубопровод тепловой магистрали (диаметр 20 см) защищенный изоляцией толщиной 10 см отапливает рабочее помещение при этом температура трубы 160ºС, а внешнего ее покрова 30ºС. Определить распределение температуры внутри изоляции, если коэффициент теплопроводности k = 0,00017, а также количество теплоты, отдаваемой 1 м трубы.

▲ Если тело находится в стационарном тепловом состоянии и температура Т в каждой его точке есть функция только одной координаты х, то, в соответствии с законом теплопроводности Фурье, количество теплоты, испускаемое в секунду будет равно

(1)

где λ – коэффициент теплопроводности, а площадь сечения тела S(x) определяется по формуле

S(x)=2πxl,

где х– радиус трубопровода, l – длина трубы, следовательно, уравнение (1) можно записать в виде

или

(2)

Разделяя переменные в дифференциальном уравнении (2) получим

(3)

По условию задачи необходимо определить распределение температуры внутри изоляции. Поэтому сначала левую часть уравнения (3) интегрируем в пределах от 160ºС до 30ºС, а правую часть интегрируем в пределах от 10 до 20 см.

После интегрирования уравнения (3), находим

(4)

Затем, проинтегрируем левую часть уравнения (3) в пределах от 160ºС до некоторой температуры Т, а правую часть интегрируем в пределах от 10 до х см. После интегрирования уравнения (3), находим

(5)

Разделив почленно уравнение (5) на уравнение (4), получим

Из этого уравнения следует, что закон распределения температуры внутри изоляции будет иметь вид

Кроме того, по условию задачи необходимо определить количество теплоты отдаваемой 1 м трубы. Поэтому для того, чтобы выполнить условие задачи необходимо из уравнения (4) при l = 100 см выразить Q и рассчитать его значение

▲

Пример. Найти закон изменения давления куска горной массы на горизонтальную площадь р и стенки транспортной емкости р_S прямоугольной формы с возрастанием глубины h с учетом трения кусков о стенки емкости принимая во внимание, что давление куска на стенки принимается пропорциональным давлению на горизонтальную площадь р_S = kp.

▲ Рассмотрим рис.

Рис.

Выберем в емкости бесконечно тонкий слой между двумя воображаемыми плоскостями на глубине h и h+dh. Рассмотрим условия равновесия этого слоя. На первую плоскость действует давление р сверху вниз, на вторую – давление р+dp снизу в верх.

Умножая силы р и р+dp на площадь поперечного сечения S емкости, получим силу, действующую вверх.

На слой также действует собственный вес , где γ – удельный вес горной породы, dh – высота слоя.

Кроме этих сил, если открыть нижнюю заслонку емкости, в самом начале движения кусков вследствие их давления на стенки емкости возникает направленной вверх сопротивление трения.

Пусть Р – периметр сечения емкости. Тогда поверхность части стенок, ограничивающей рассматриваемый слой, будет Pdh. Поскольку величина dh бесконечно малая, то боковое давление на единицу площади в пределах этого слоя можно принять постоянным.

Полное боковое давление равно kPpdh, а вызванное им трение μkPpdh, где μ – коэффициент трения.

Условие равновесия всех действующих сил определяется уравнением

или

. (1)

Обозначив , получим окончательный вид дифференциального уравнения

,

или

. (2)

Интегрируя это уравнение, получим

,

или

Применяя операцию обратную логарифмированию, получим

(3)

Так как, при h = 0 давление отсутствует р = 0, т.е. начальные условия имеют вид

р(0)=0, (4)

то удовлетворяя в решении (3) начальным условиям (4) определим значение произвольной постоянной

, Подставляя значение С в решение (3), получим

(5)

Из уравнения (5) выразим р

И подставив в него , получим

(6)

Так как по условию задачи р_S = kp, то запишем окончательный вид решения

(7)

Заметим, что из (6) и (7) видно, что давления р_S и p возрастают непропорционально глубине h. ▲

Пример. Кусок горной массы массой m сбрасывается вниз по рудоспуску. Найти закон изменения скорости падения v этого куска, если на него действует сила тяжести и тормозящая сила сопротивления воздуха, пропорциональная скорости.

▲ Задача заключается в определении закона изменения скорости v с течением времени t, т.е. v = f(t).

Запишем второй закон Ньютона

где - ускорение движущегося куска, F – сила действующая на этот кусок в направлении движения.

Сила F складывается из двух сил: силы тяжести F₁ = mg направленной вниз и силы сопротивления воздуха F₂ = - kv направленной вверх.

Таким образом, уравнение движения куска будет иметь вид

В этом дифференциальном уравнении разделив переменные, получим

(1)

Интегрируя уравнение (1) найдем

(2)

Разрешим (2) относительно v

(3)

Обозначив , придем к уравнению

(4)

Если известна начальная скорость падения куска, то можно вычислить значение произвольной постоянной С. Пусть заданы начальные условия: скорость движения куска в начальный момент времени t = 0 равна v₀, тогда

(5)

Подставляя (5) в решение (4) окончательно получим вид искомой функции

. ▲

Пример. Конвейерная лента огибает барабан радиуса r и нагружена силами F₀ и F₁, так, что (рис.). Благодаря трению между барабаном и лентой даже значительно меньшая сила F₀ может уравновешиваться большей силой F₁. Необходимо найти наибольшую силу F₁, которая может уравновешиваться силой F₀ , если коэффициент трения равен μ.

▲ Рассмотрим рис.

Рис.

Пример 16. Рассмотрим вентиляцию забоя объемом V(м³), в котором в процессе проведения работ накапливаются вредные газообразные выделения в количестве Z в час. Пусть обмен воздуха в течении 1 часа составляет М (м³/ч), причем приточный воздух содержит вредные вещества в концентрации  на 1 м³. Требуется найти концентрацию Z (на 1 м³) вредных выделений в забое через время t после начала работы, если начальное значение этой концентрации (остаток загрязнений от предыдущей смены) составляет Z₀.

▲ За малый промежуток времени dt концентрация вредных выделений Z увеличивается на dZ. Следовательно общее количество выделений составит VdZ и оно будет состоять из выделений, принесенных приточным воздухом - Мdt, и выделений образовавшихся в процессе работы - Zdt за вычетом количества вредных выделений, которое содержалось в извлеченном из забоя за время dt воздухе. Предположим, что за малый промежуток времени dt изменение концентрации вредных выделений равно – ZМdt. Следовательно, уравнение вентиляции забоя имеет вид:

или

Полученное уравнение является линейным неоднородным уравнением, которое будем решать, используя сразу формулу общего решения (1.51):

или

.

Удовлетворяя начальному условию , определим значение произвольной постоянной . Таким образом, окончательное решение исходной задачи имеет вид:

.▲

Пример . Определить уравнение кривой, по которой распола­гается уровень грунтовых вод вблизи скважины, простираю­щейся до непроницаемого слоя (рис.).

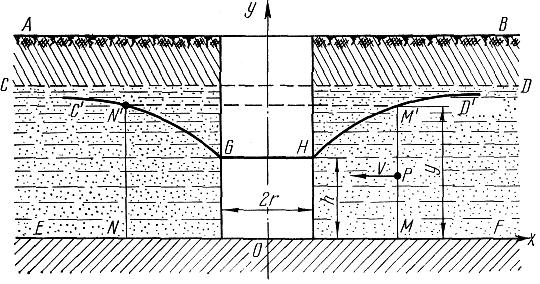
Рис.

▲ Пусть АВ — поверхность земли; CD — поверх­ность грунтовых вод до устройства колодца; EF — водонепроницае­мый слой, ограничивающий снизу поток грунтовых вод.

Если высота воды в скважине поддерживается откачкой на постоянном уровне GH, то поверхность грунтовых вод вблизи от колодца понижается определенным образом.

Линия поверхности грунтовых вод CD переходит в две искрив­ленные ветки C'G и D'H, которые замыкаются на уровне воды GH. Поверхность уровня грунтовых вод представляет собой поверхность вращения вокруг оси Оу меридиональной линии GC' или HD'.

Кривая HD' определяется на основании эмпирического прави­ла, по которому скорость v течения воды в точке Р пропускающего (дренирующего) грунта пропорциональна наклону кривой в точ­ке М', лежащей на вертикали точки Р.

Обозначая коэффициент пропорциональности через k, получим выражение скорости:

.

Через боковую поверхность цилиндра радиально внутрь протекает количество воды, определяемое дифференциальным уравнением

, (1)

которое для всего цилиндра радиуса х равно расходу воды в скважине.

Разделим переменные в дифференциальном уравнении (1):

,

Интегрируя, получим

(2)

Постоянную интегрирования находим из условия, что кривая поверхности D'H переходит в поверхность скважины GH.

Если диаметр скважины 2r, а глубина воды в ней h, то при x=r y=h, т.е.

или

(3)

Постоянную интегрирования (3) вводим в уравнение (2) и получаем уравнение искомой кривой

или

. ▲

Пример . Через сосуд емкостью а л, наполненный водным раствором некоторой соли, непрерывно протекает жидкость, причем в единицу времени втекает b л воды и вытекает такое же количество раствора. Найти закон изменения содержания соли в сосуде в зави­симости от времени протекания жидкости через сосуд.

▲ В данный момент времени t в сосуде содержится х кг соли, следовательно, в каждом литре раствора содержится x/a кг соли, а в b литрах bx/a кг.

Если бы в течение единицы времени, начиная с момента t, концентрация раствора оставалась неизменной, какой она была в мо­мент t, то количество соли в сосуде за эту единицу времени уменьшилось бы на bx/a кг; такова скорость уменьшения количества соли сосуде для момента t.

С другой стороны, производная

равна скорости прироста количества соли в момент t, поэтому ско­рость уменьшения количества соли в момент t равна — .

Итак,

Разделяя переменные, получим

откуда

Потенцируя, найдем

(1)

где C — произвольная постоянная.

Предположим, что в некоторый начальный момент t=0 коли­чество соли в сосуде равно A кг.

Полагая в равенстве (1) t = 0, найдем

C = A.

Искомый закон изменения содержания соли

.▲

Растворение твердых тел

Пусть при постоянной температуре скорость растворения твер­дого тела в жидкости пропорциональна количеству этого вещества, еще могущего раствориться до полного насыщения жидкости.

Пусть Р — количество вещества, дающее насыщенный раствор; х — количество растворившегося вещества.

Тогда дифференциальное уравнение процесса

где k — эмпирический коэффициент пропорциональности, t — время. Разделяя переменные и интегрируя, находим

(1)

Начальное условие: при t = 0 х = 0, откуда

и постоянная интегрирования

C = -P (2)

Подставляем выражение (2) в общее решение (1) и получаем закон зависимости количества растворившегося вещества от вре­мени:

Задача 54. Резервуар наполнен 75 л суспензии, содержащего 3 кг растворенного реагента. Приток воды составляет 4 л в минуту, а рас­ход смеси из сосуда 2 л в минуту. Концентрация поддерживается равномерной посредством перемешивания (рис.). Найти количе­ство реагента, которое будет содержаться в резервуаре через 25 мин.

Рис.

▲ Пусть х — количество реагента в резервуаре в мо­мент t, кг; t — время, отсчитываемое от начального момента t₀, мин; —dx — количество реагента, выходящее из резервуара за время dt (знак минус обусловлен тем, что х — убывающая функция вре­мени), кг.

К моменту t в резервуар поступило 4t л воды и вышло 2t л суспензии. Увеличение суспензии составляет 2t л.

Таким образом, общее количество жидкости достигло 75+2t л и в ней растворилось х кг реагента.

За время dt уходит –dx кг реагента и 2dt л суспензии.

Считая концентрацию суспензии постоянной, получим количество реагента в одном литре кг. Следовательно, за короткий промежуток времени dt количество реагента уменьшится на кг.

Итак, элементарное уравнение движения жидкости будет иметь вид

Разделяя переменные в этом уравнении, имеем:

.

Интегрируя это уравнение, с учетом того, что в начальный момент времени t₀ = 0 в резервуаре было 3 кг реагента (х₀ = 3 кг), а через 25 мин, т.е. в момент времени t₁ = 25 сек, его стало х₁ = х кг, получим

или

Потенцируя полученное выражение, получаем

,

или искомое количество реагента в резервуаре будет равно

кг. ▲

Пример. Подвергая 10 кг соли действию 90 л воды, обнару­жили, что в течение часа растворилась половина этого количества.

Считая концентрацию насыщенного раствора соли равной 1/3, най­ти количество растворенной соли в течение часа, если за это время было влито 180 л воды.

▲ Скорость уменьшения нерастворенного вещества должна быть пропорциональна х и С₀ – C_t, что приводит к дифференциальному уравнению

где k (предполагается, что k > 0) —коэффициент пропорциональ­ности, подлежащий определению.

В правой части поставлен знак минус, так как каждый из мноdx жителей k, х, С₀–C_t, через произведение которых выражается , положителен, в то время как < 0, поскольку с течением времени количество нерастворенного вещества должно убывать.

Преобразуя произведение этих множителей и выражая C_t че­рез М, V и х, получаем

Пусть

(1)

Тогда

и искомое дифференциальное уравнение задачи принимает вид

(2)

Начальное условие:

при t=0 x=M. (3)

Условие для определения коэффициента а:

при t=1 ч х=M/2. (4)

Разделяя переменные в уравнении (2) и интегрируя, имеем

(5)

Разложим подынтегральное выражение первого интеграла на простейшие дроби:

Теперь, умножив обе части уравнения (5) на b, можем записать

,

потенцируя, получим

(6)

Полагая в уравнении (6) t=0 и принимая во внимание началь­ное условие (3), находим

(7)

Тогда уравнение (6) примет вид

Решая последнее равенство относительно х, имеем

или

откуда общее решение

(8)

Выполним проверку: полагая в уравнении (8) t=0, получим

.

т. е. начальное условие соблюдается.

Дифференцируя уравнение (8) по t, найдем

.

Составим с помощью уравнения (7) выражение

.

Итак,

.

По условию М=10 кг, V=90 л, С₀=1/3, поэтому по второму из соотношений (1)

Равенство (8) примет вид

.

Согласно условию (4), откуда

Согласно первому из соотношения (1),

k=0,0255·90=2,295

При V=180 л

a = 0,0255 : 2 = 0,01275; b = (180:3) – 10 = 50; a·b =0.6375

Искомое количество растворившейся соли

.

Следовательно, количество растворенной соли в течение часа равно М—х= 5,2 кг. ▲

Задача 58. В процессе зарядки коронным разрядом в воздушной или газовой среде происходит процесс ионизации, при котором за 1 сек обра­зуется q положительных и q отрицательных ионов в данном объеме газа. Так как положительные и отрицательные ионы снова соеди­няются между собой, то количество их убывает. Из общего количе­ства п положительных ионов в каждую секунду соединяется часть, пропорциональная квадрату их количества. Коэффициент пропор­циональности k зависит от природы и состояния газа. Найти зави­симость количества ионов п от времени t.

▲ Непосредственно из условия можно записать диф­ференциальное уравнение процесса ионизации

(1)

После разделения переменных в уравнении (1) получаем

или

Приведем уравнение к виду

. (2)

Найдем общий интеграл уравнения (2)

откуда после потенцирования имеем

Следовательно, общее решение принимает вид

(3)

С учетом начального условия: при t = 0 п = 0, определим значение произвольной постоянной С.

откуда

С = 1

Подставляя найденное значение постоянной интегрирования в уравнение (3), получаем искомый закон

. ▲

Пример (одн.ур). Для равномерного освещения кусков рудной массы при реализации процесса фотометрической сепарации необходимо определить форму зеркала, чтобы отраженные от него лучи были параллельны оси Ох. Источник света помещен в точке О (Рис.).

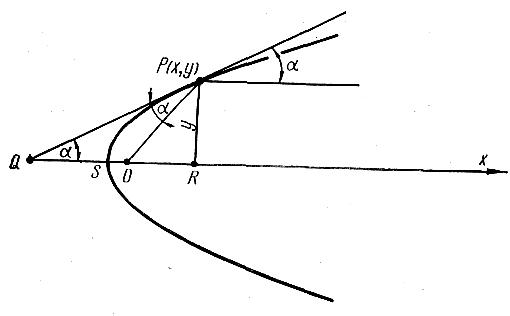
Рис.

▲ Рассмотрим кривую сечения поверхности зеркала плоскостью хОу и на этой кривой произвольную точку Р(х,у) (рис.). Угол падения луча равен углу отражения и поэтому OQP = α.

Так как OQP = α, то Δ OPQ — равнобедренный. Таким об­разом,‌ .

Считая у>0, получаем

Умножая числитель и знаменатель дроби на выражение , имеем

откуда

или

Проинтегрировав последнее равенство, получаем

или

(1)

По условию кривая должна быть симметричной относительно оси Ох, т. е. уравнение (1) будет выполняться и при у<0. Равен­ство (1) показывает, что искомая кривая есть парабола с осью сим­метрии Ох.

Пусть дано расстояние от источника света О до центра зер­кала S: . Тем самым получаем начальное условие:

_{при х = -а у = 0 (2)}

Подставляя эти значения в уравнение (1), имеем

откуда

С = 2а.

Значение С=0 не подходит по физическому смыслу задачи. Таким образом, искомая парабола:

Для этой параболы р = 2а и, следовательно, фокусное расстоя­ние р/2=а, т. е. источник света О находится в фокусе. Плоскость хОу, в которой лежит парабола , проходит через ось Ох. Уравнение параболы не изменится, если эту плоскость вра­щать вокруг оси Ох. Это значит, что поверхностью зеркала будет служить параболоид вращения. Этот параболоид в сечении с любой плоскостью, проходящей через ось Ох, будет давать параболу, урав­нение которой найдено выше. ▲