23. Оценка значимости коэффициентов уравнения парной линейной регрессии, построение доверительных интервалов.

Чтобы сделать стат выводы о значим коэф модели, необх рассч остаточн дисперсию.Она рассч на этапе провед анализа. = = – остаточн. дисперсия. Станд ошибка модели - = .

Использ критерий Стьюдента: Т= . S_a0 =

Критическое значение нах из табл распред Стъюдента при выбр ур-не значимости альфа и числе степеней свободы Ткрит.

25. Условия Гаусса-Маркова. Теорема Гаусса-Маркова

Условия

I. Регрессионная модель линейна по параметрам (коэффициентам), корректно специфицирована, и содержит аддитивный случайный член.

II. Случайный член имеет нулевое среднее.

III. Все объясняющие переменные не коррелированны со случайным членом.

IV. Наблюдаемые значения случайного члена не коррелированны друг с другом.

V. Случайный член имеет постоянную дисперсию

VI. Ни одна из объясняющих переменных не является строгой линейной функцией других объясняющих переменных.

VII. Случайный член распределен нормально (необязательное, но часто используемое условие).

Рассматривается модель парной регрессии, в которой наблюдения У связаны с Х следующей зависимостью: . На основе выборочных наблюдений оценивается уравнение регрессии . Теорема Гаусса—Маркова гласит:

Если данные обладают следующими свойствами:

Модель данных правильно специфицирована;

Все Хi детерминированы и не все равны между собой;

Ошибки не носят систематического характера;

Дисперсия ошибок одинакова и равна некоторой б² ;

Ошибки некоррелированы;

— то в этих условиях оценки метода наименьших квадратов эффективны в классе линейных несмещённых оценок.

26) Линейная модель множественной регрессии.

Теоретическая модель имеет след вид У= α₀ + α₁Х + α₂ + α₃Х…+ α_mХ_m + ε. По данным выборки:

У_i= α₀ + α₁x_i1 + …+ α_mx_im + е_i. В связи с большим объемом выбоки все вычисления производятся только в матричной форме. Тогда ур-ие переписывается в виде у=ХА+ε. Для вычисления оценок параметров пользуются методом наименьших квадрантов. Метод наименьших квадратов (— один из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным. Метод основан на минимизации суммы квадратов остатков регрессии.

у с крышечкой=А с крышечкой ∙ Х.

е= у – у с крышечкой=у- Ас крышечкой ∙Х

Выполним дифференцирование по вектору Ас крышечкой и преобразуем. Получаем, что система нормальных уравнений имеет вид Х^Т∙ХАс крышечкой=Х^Т∙У. Предположим матрица

Х^Т∙У – нвырожденная , тогда получаем Ас крыш=(Х^Т∙Х)^-1∙Х^Т∙у - формула для расчета оценок коэф множеств регрессии.

27.Св-во оценок МНК для модели множественной регрессии и показатели кач-ва подборарегрессии:коэф.множественнойкорелляции,коэф.частнойкорелляц,коэф.множнств.детерминац.Множественная регрессия—уравнение связи с несколькими независимыми переменными . Наиболее распространенной в эконометрике является линейная модель множественной регрессии. ,где  — параметры уравнения регрессии, подлежащие оценке, — случайная ошибка.По выборке ограниченного объема оценивается выборочное уравнение регрессии: , где — оценки параметров .Данные выборки можно представить в матричной форме: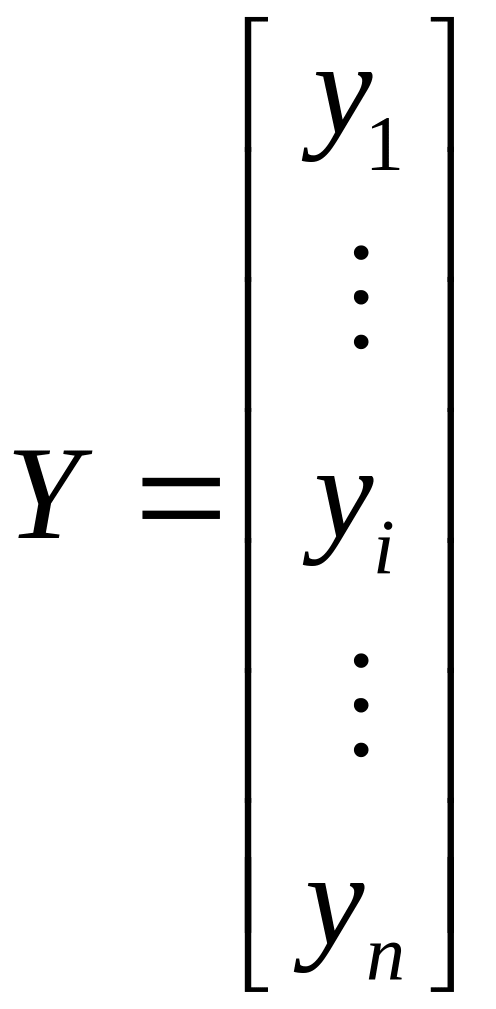  — вектор значений зависимой переменной размерности ;  — значение переменной в наблюдении ;  — матрица значений независимых переменных размерности ,  — значения переменных в наблюдении . Первый столбец этой матрицы является единичным, так как в уравнении (1) присутствует свободный член.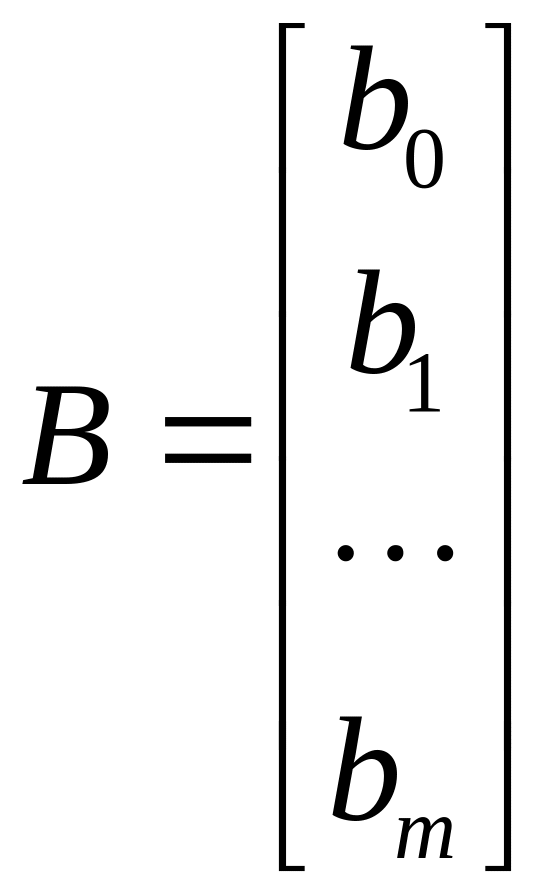  — вектор оценок параметров модели размерности .Для оценки параметров модели применяют метод наименьших квадратов (МНК). Для линейных и нелинейных уравнений, приводимых к линейным, строится система из линейного уравнения с неизвестным, называемая системой нормальных уравнений. Количество уравнений равняется количеству неизвестных переменных, поэтому решение системы можно найти, например, с помощью метода Крамера. Формулы Крамера где — определитель системы, — частные определители, которые получаются путем замены соответствующего столбца матрицы определителя системы столбцом свободных членов.Решением системы нормальных уравнений в матричной форме будет вектор оценок коэффициент множественной детерминации , который измеряет долю дисперсии, совместно объясненной независимыми переменными, и определяется по формул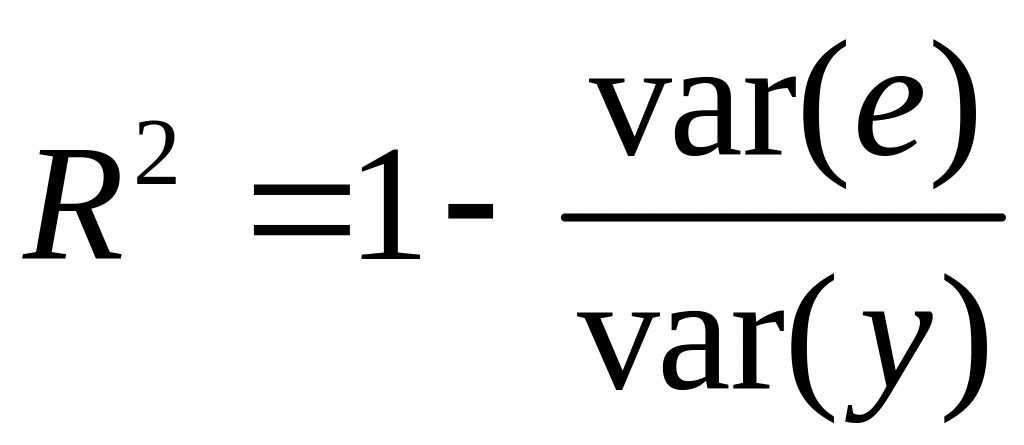е , , где — общая дисперсия результативного признака; остаточная дисперсия.Скорректированный коэффициент множественной детерминации содержит поправку на число степеней свободы и дает такую оценку тесноты связи, которая не зависит от числа факторов в модели. Он рассчитывается по формулам (7) или (8)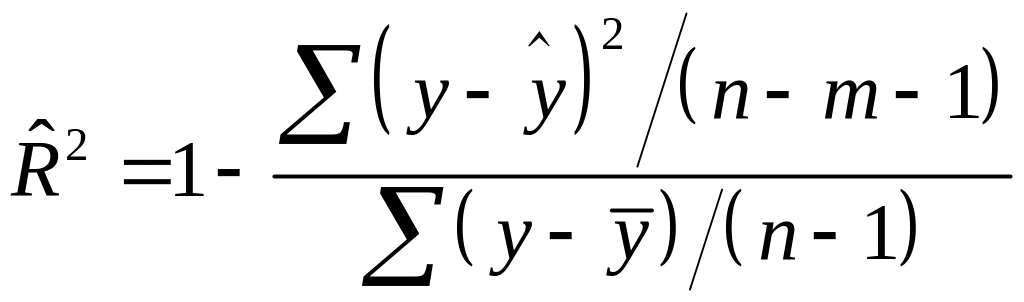 , ,где -число независимых факторов; – число наблюдений. Чем больше величина , тем сильнее различия и . Квадратный корень из коэффициента множественной детерминации называется коэффициентом множественной корреляции. При линейной зависимости коэффициент множественной корреляции можно определить через матрицу парных коэффициентов корреляции: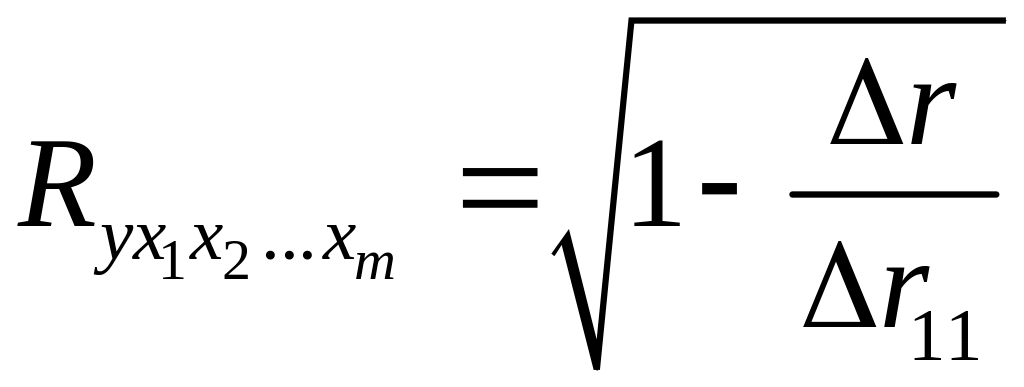 , где частных коэффициентов корреляции (для линейных связей), которые характеризуют тесноту связи между результатом и соответствующим фактором при устранении влияния других факторов, включенных в уравнение регрессии.При двух факторах формулы для расчета коэффициентов примут вид: ; .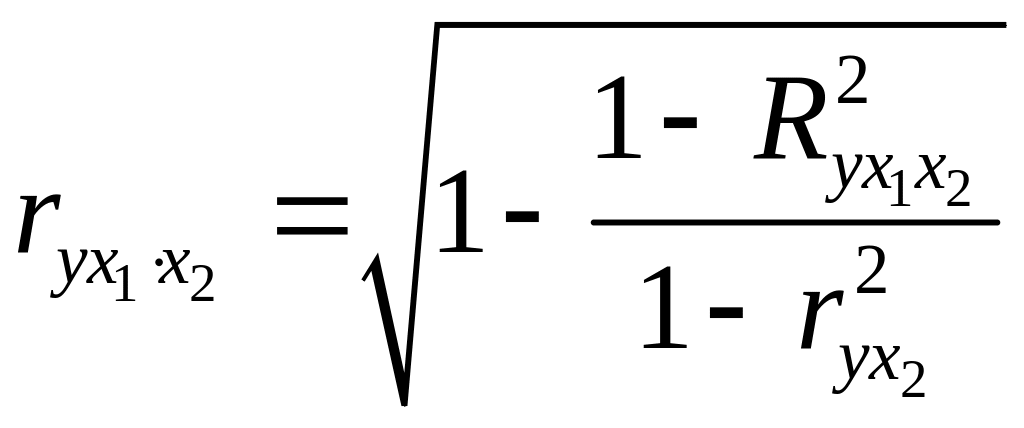

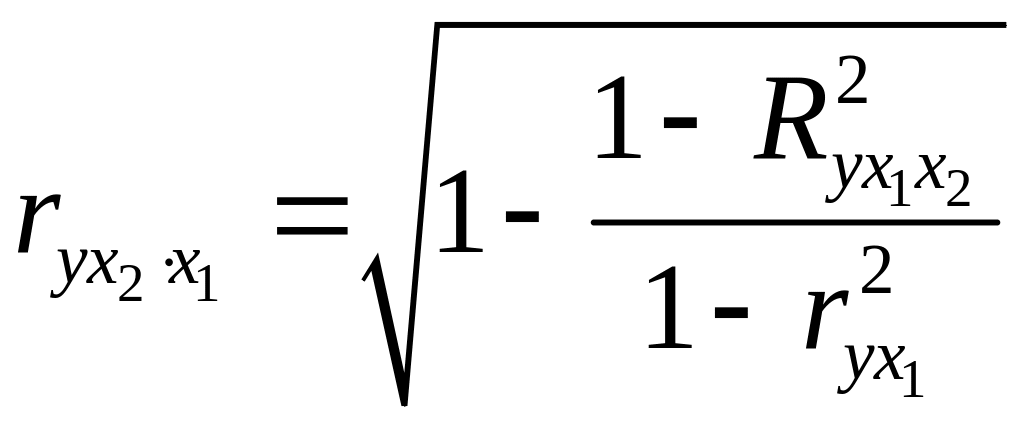28. Мультиколлинеарность факторов. Признаки мультикол. и способы ее устран. Понятием коллениарность обозначим связь между двумя экзогенными переменными( ), эндоген(Y). Понятием мультиколл.обозначим лин-ую связь между более чем 2-мя экзоген. переменными. Мультикол.-это корр-ть 2-х или неск. экзог. переменных. Различают строгую мультикол., когда между перемен. сущ ли-ая функцион. зависимость.и нестрогую мультикол., когда между перемеными сущ. лин-ая коррел. связь. Причины возн-ия мультикол-ти: включ. в выборку 2-х зависимых между собой перем. или включ. в выборку переменной, кот. сильно коррелирует с эндоген. переменной. В результате колл-ти увелич. стандартн. ошибки коэф. и поэтому дроби Стьюдента, то сама дробь оказывается занесенной и коэф. ошибочно признаются значимыми. Коэффициенты в модели оказываются сильно коррелируемыми друг с другом, что лишает смысла их эк. интер-ию. Для проверки наличия мультикол-ти исп-ся матрица коэф-ов парной корреляции. Коэф. этой матрицы сравн-ся: если | |≥0,8, то из модели иссл. тот фактор, у которого меньше модуль | | или| |. если имеет место мульти-ть, мы вычесл определитель . Чем ближе к 0 тем сильнее мульти-ть факторов и наооборот чем ближе к 1 определитель , тем меньше мультикол-ть факторов. Для устранения этого явл следует: изм или увелич объем выборки; увел. вариацию факторов x; искл. из модели переменную, имеющую наиб выс коэф-ты корреляции.