Гистограмма относительных частот

Для наглядности строят различные графики статистического распределения.

По данным дискретного вариационного ряда строят полигон частот или относительных частот.

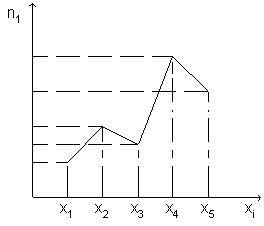
Полигоном частот называют ломанную, отрезки которой соединяют точки (x₁; n₁), (x₂; n₂), ..., (x_k; n_k). Для построения полигона частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им частоты n_i. Точки ( x_i; n_i) соединяют отрезками прямых и получают полигон частот (Рис. 1).

Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x₁; W₁), (x₂; W₂), ..., (x_k; W_k). Для построения полигона относительных частот на оси абсцисс откладывают варианты x_i, а на оси ординат - соответствующие им относительные частоты W_i. Точки ( x_i; W_i) соединяют отрезками прямых и получают полигон относительных частот.

В случае непрерывного признака целесообразно строить гистограмму.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению n_i / h (плотность частоты).

Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии n_i / h.

Площадь i - го частичного прямоугольника равна hn_i / h = n_i - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношениюW_i / h (плотность относительной частоты).

Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии W_i / h (Рис. 2).

Площадь i - го частичного прямоугольника равна hW_i / h = W_i - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. 

Рис. 1. Полигон частот

Рис. 2. Гистограмма относительных частот

Числовые характеристики вариационных рядов

 

          Для единообразия формул будем обозначать х_i выборочное значение независимо от того, в каком из вариационных рядов оно находится.

 

     Начальным выборочным моментом порядка r называют число

.

     Центральным выборочным моментом порядка r называют число

 .

          Моменты порядков r = 1  и  r = 2  наиболее употребительны и носят специальные названия и обозначаются особо.

          Момент m₁ (порядка 1) обозначается   и носит название выборочного среднего

          Свойства выборочного среднего аналогичны свойствам математического ожидания, одно из них выглядит так:

                                                 .                                          (20.1)

          В самом деле, значения вариационного ряда для выборки из генеральной совокупности а + b будут таковы:  ; частоты при этом остаются теми же. Поэтому

.

          Центральный момент порядка 1 всегда равен 0. Центральный момент порядка 2 называют выборочной дисперсией и обозначают  :

.

          Свойства выборочной дисперсии аналогичны свойствам дисперсии. Например,

                    .                                                                             (20.2)

 

          В самом деле,

 

          При вычислении на практике удобно пользоваться такой формулой:

 

                              .                                    (20.3)