
- •1.Декартова и полярная системы координат на плоскости. Формулы,связующие координаты точки в этих системах. Декартова система координат в пространстве.
- •2.Понятие геометрического вектора. Основные определения связанные с этим понятием (длина вектора, равенство векторов, нуль-вектор, коллинеарные и компланарные векторы, орт вектора).
- •3.Линейниые операции с геометрическими векторами. Законы, которым удовлетворяют эти операции. Разность векторов. Коллинеарные векторы.
- •4.Деление отрезка в заданном отношении.
- •5. Понятие радиус-вектора. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •6.Действия с геометрическими векторами в координатной форме.Признак коллинеарности векторов.
- •7.Скалярное произведение геометрических векторов и его свойства. Признак ортогональности векторов.
- •8.Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками. Вычисление косинуса угла между двумя точками.
- •9. Направляющие косинусы вектора и их свойства.
- •10.Векторное произведение: определение ,вычисление и свойства.
- •11. Смешанное произведение: определение, вычисление, геометрический смысл.
- •12. Общее уравнение прямой на плоскости и его исследование.
- •13. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых
- •18.Различные виды уравнений прямой в пространстве ( каноническое, параметрическое, общее уравнение прямой).
- •19.Условия параллельности и перпендикулярности прямых в пространстве.
- •20. Условия параллельности и перпендикулярности плоскости и прямой в пространстве.
- •21.Угол между прямой и плоскостью.
- •22.Окружность и ее уравнение.
- •23.Определение эллипса и его каноническое уравнение.
- •24. Определение гиперболы и ее каноническое уравнение.
- •25.Определение параболы и ее каноническое уравнение.
- •27.Действия с матрицами (сложение, умножение на скаляр, перемножение матриц, транспонирование матриц). Законы, которым эти действия удовлетворяют.
- •28. Определение определителя и его свойства.
- •29.Определитель, минор и алгебраическое дополнение элемента определителя.
- •30.Обратная матрица. Теорема о существовании и единственности обратной матрицы.Способы вычисления обратной матрицы.
- •3) Способы вычисления обратной матрицы:
- •А) Метод Гаусса—Жордана
- •Б) с помощью матрицы алгебраических дополнений
- •В) Методы Шульца
- •31. Определение ранга матрицы. Базисный минор. Вычисление ранга матрицы с помощью элементарных преобразований.
- •3) Вычисление ранга матрицы с помощью элементарных преобразований.
- •32)Система линейных уравнений и её решение. Различные формы записи линейных уравнений. Определение однородной, неоднородной, совместной, несовместной, определённой и неопределённой систем.
- •А) Векторная форма записи
- •Б) Матричная форма записи
- •33)Матричный способ решения систем линейных уравнений. Пример решения неоднородной слау
- •34) Формулы Крамера.
- •35) Теоре́ма Кро́некера — Капе́лли
- •36)Условия определённости и неопределённости систем линейных уравнений
- •37)Решение систем линейных уравнений метод Гаусса
- •38)Теорема о совместимости однородной системы линейных уравнений
- •39)Теорема о существовании ненулевых решений однородных линейных уравнений.
- •40)Линейное векторное пространство. Пространство r и линейные операции в этом пространстве.
- •41) Скалярное произведение n-мерных векторов. Неравенство Коши-Буняковского
- •42)Определение линейно зависимых и независимых векторов. Критерий линейной зависимости и не зависимости веторов в
- •2) Критерий линейной зависимости векторов
- •43) Базис линейного пространства. Примеры базисов в
- •44. Теорема о единственности разложении вектора линейного пространства по базису.
- •45.Подпространство линейного пространства. Линейная оболочка системы векторов. Сумма и пересечение подпространств. Примеры подпространств.
- •46.Собственные числа и собственные векторы квадратной матрицы и их свойства.
- •47.Характерестическое уравнение , соответствующие квадратной матрице . Теорема о связи собственных чисел матрицы с корнями этого уравнения.
- •48. Линейные операторы. Основные понятия.
- •49. Комплексные числа в алгебраической форме записи .Геометрическое изображение комплексных чисел. Действия с комплексными числами в алгебраической форме записи .Решение алгебраических уравнений
- •50.Тригонометрическая и показательная форма записи комплексных чисел.Модуль и аргумент комплексного числа. Формула Эйлера.
- •51. Действия с комплексными числами. Формула Муавра
- •52)Линейная балансовая модель
- •53) Квадратные формы. Критерий Сильвестра
- •Определение
- •Связанные определения
- •Свойства
- •Критерий положительной определённости квадратичной формы
- •Критерий отрицательной определённости квадратичной формы
12. Общее уравнение прямой на плоскости и его исследование.
Общее уравнение прямой.
Ах+Ву+С=0
А,В,С- произвольные числа, А и В не равны нулю одновременно. Два случая:
В=0, то уравнение имеет вид Ах+С=0, причем А не равно 0, т.е х= -С\А, это есть уравнение прямой , параллельной оси Оу, проходящей через точку (-С\А;0)
В не равно нулю, получаем у= -А\Вх-С\В. Это уравнение прямой с угловым коэффициентом к=tga=-А\В
Частные случаи общего уравнения прямой:
А=0, уравнение приводится к виду у=-С\В. Это есть уравнение прямой , параллельной оси Ох;
В=0, то прямая параллельна оси Оу;
С=0, то получаемАх+Ву=0. Уравнению удовлетворяют координаты точки О (0;0), прямая проходит через начало координат
13. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых
Простейшей из линий является прямая. Разным способам задания прямой соответствуют в прямоугольной системе координат разные виды ее уравнения.
Уравнение прямой с угловым коэффициентом.
У = кх+в, число к= tga-угловой коэффициент прямой, а уравнение- уравнение прямой с угловым коэффициентом. Если прямая проходит через начало координат , то b=0, и уравнение этой прямой будет иметь вид у= кх.
Если прямая параллельна оси Ох, то а=0,следовательно к=tga=0 и уравнение примет вид у= b.
Если уравнение прямой параллельно оси Оу, то а=∏\2, следовательно уравнение теряет смысл, т.кtg ∏\2- не существует, уравнение прямой будет иметь вид х=а, где а-абсцисса точки пересечения прямой с осью Ох.
Пучок прямых.Через точку А1(х1;у1) проходит множество прямых, именуемое центральным пучком(или просто пучком). Точка а1- центр пучка. Каждую из прямых пучка можно представить уравнением:
у-у1= к(х-х1)
к- угловой коэффициент, параметр пучка, характеризует направление прямой, она меняется от одной прямой пучка к другой. Значение параметра К можно найти, если дано еще какое-либо условие, которое определит положение прямой
14. Уравнение прямой, проходящей через две заданные точки на плоскости и в пространстве.

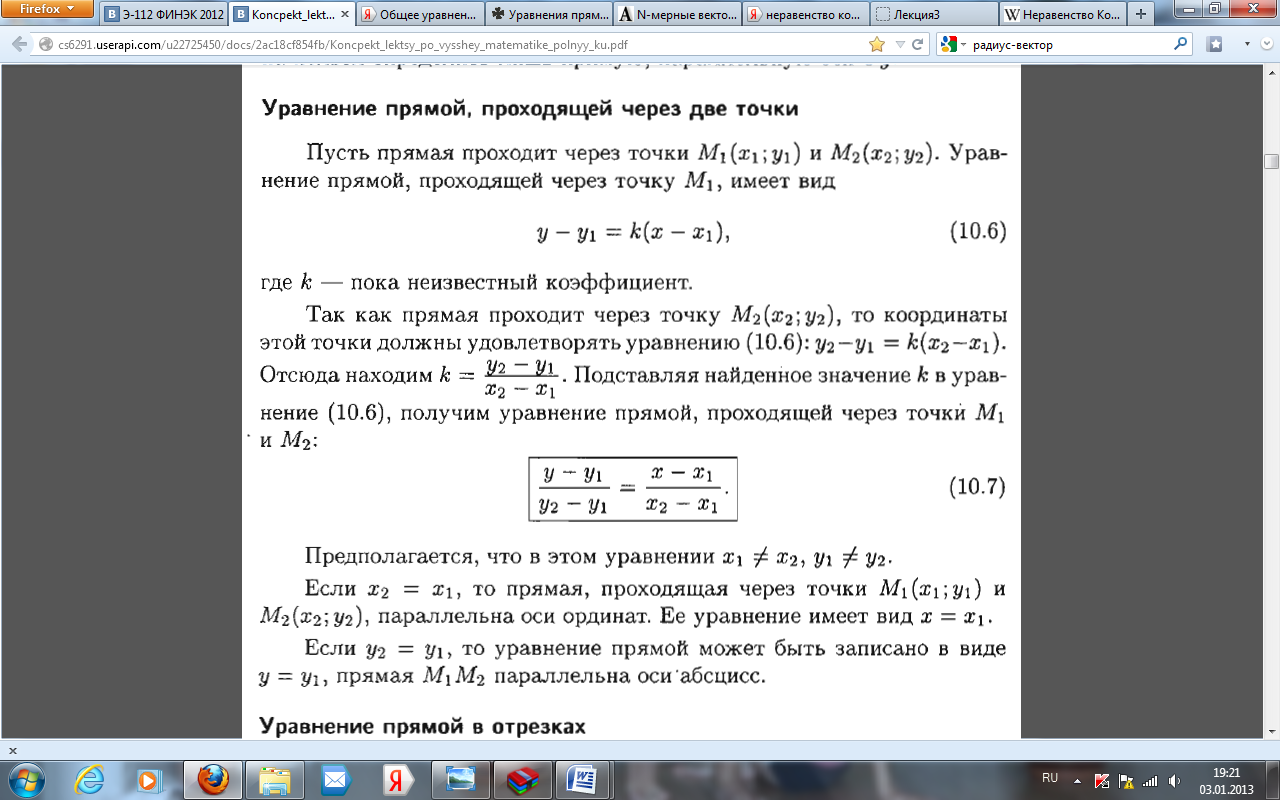
15.Угол между прямыми. Условия параллельности и перпендикулярности прямых на плоскости.
Пусть две перпендикулярные прямые L1,L2 представляются уравнениями:
y=к1x+b1,
y=к2x+b2
Тогда
формула:
![]() дает угол, на который надо повернуть
первую прямую, чтобы она стала параллельной
второй.
дает угол, на который надо повернуть
первую прямую, чтобы она стала параллельной
второй.
Условием параллельности двух прямых является равенство двух угловых коэффициентов: к1=к2
Условием перпендикулярности прямых является равенство к1*к2=-1
16. Общее уравнение плоскости и его исследование
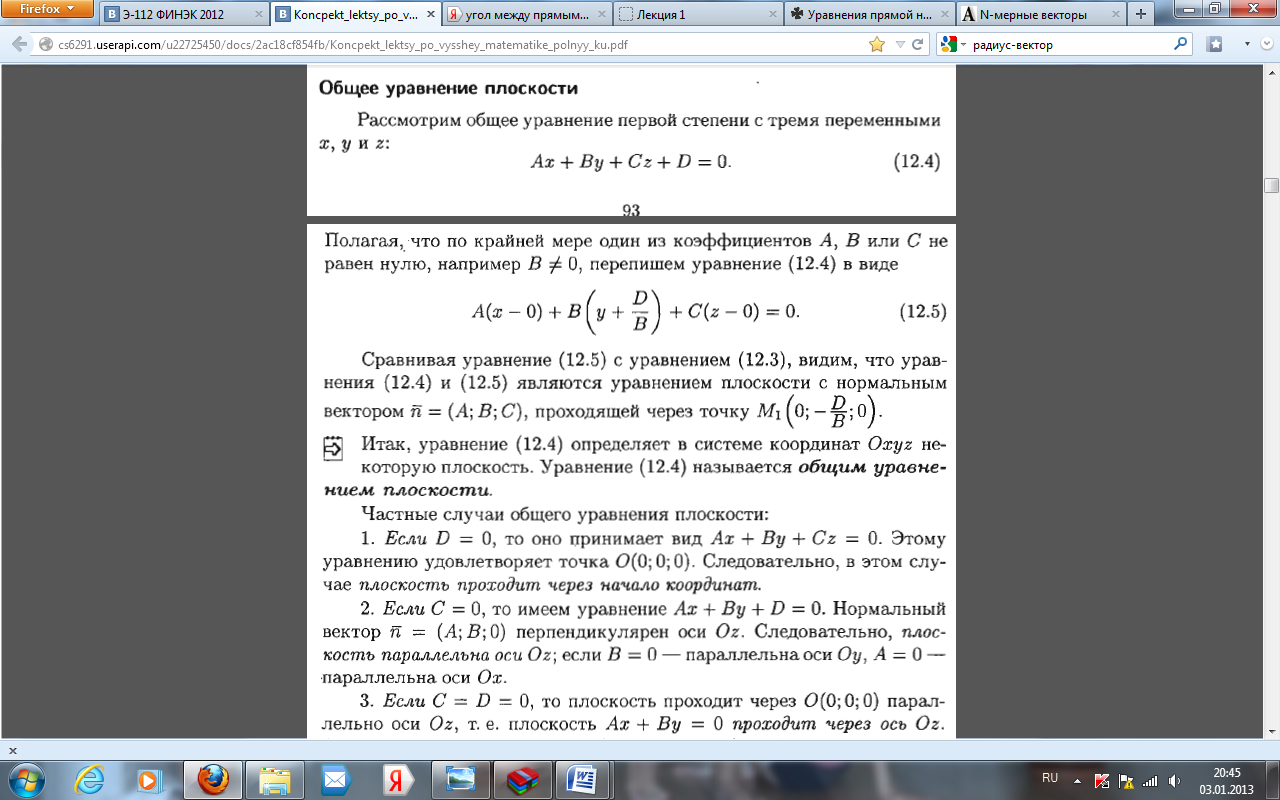
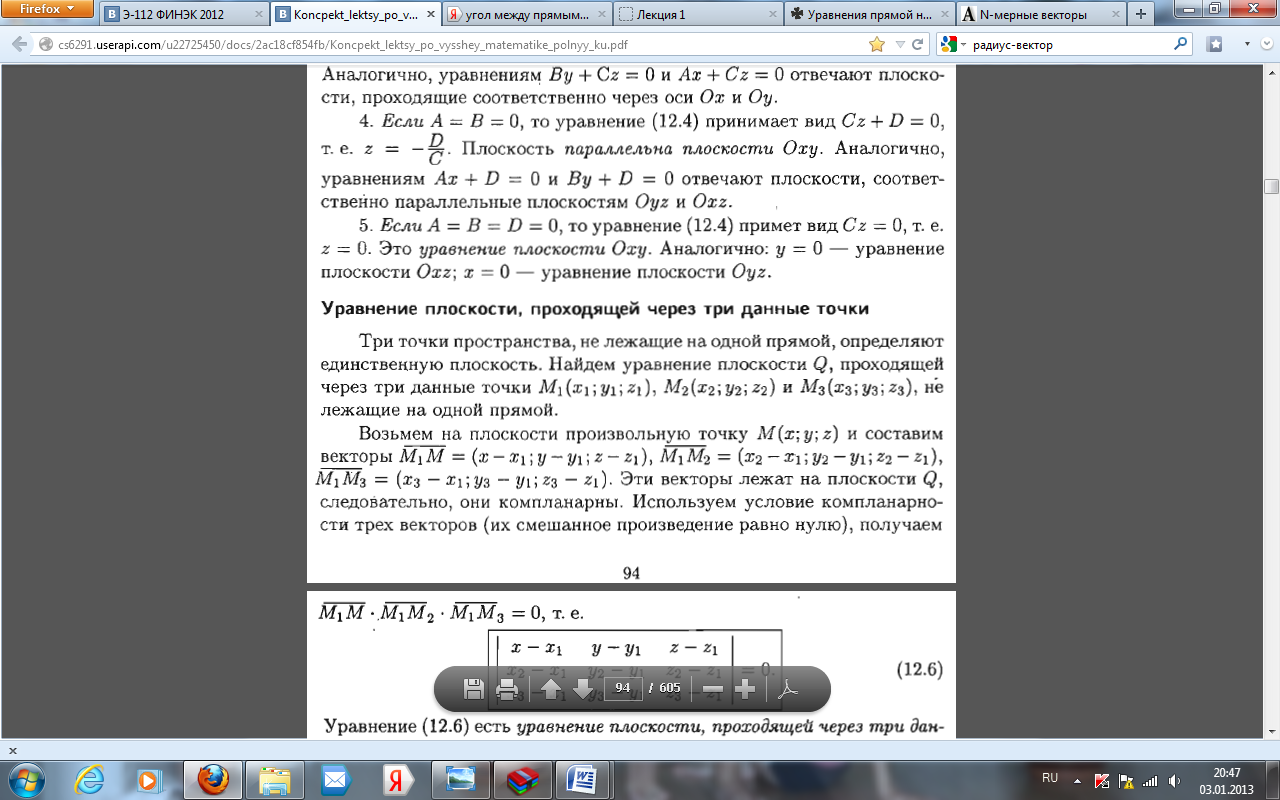
17.Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.
Угол
между двумя пересекающимися плоскостями
равен углу между прямыми, по которым
они пересекаются с любой плоскостью,
перпендикулярной их линии пересечения.
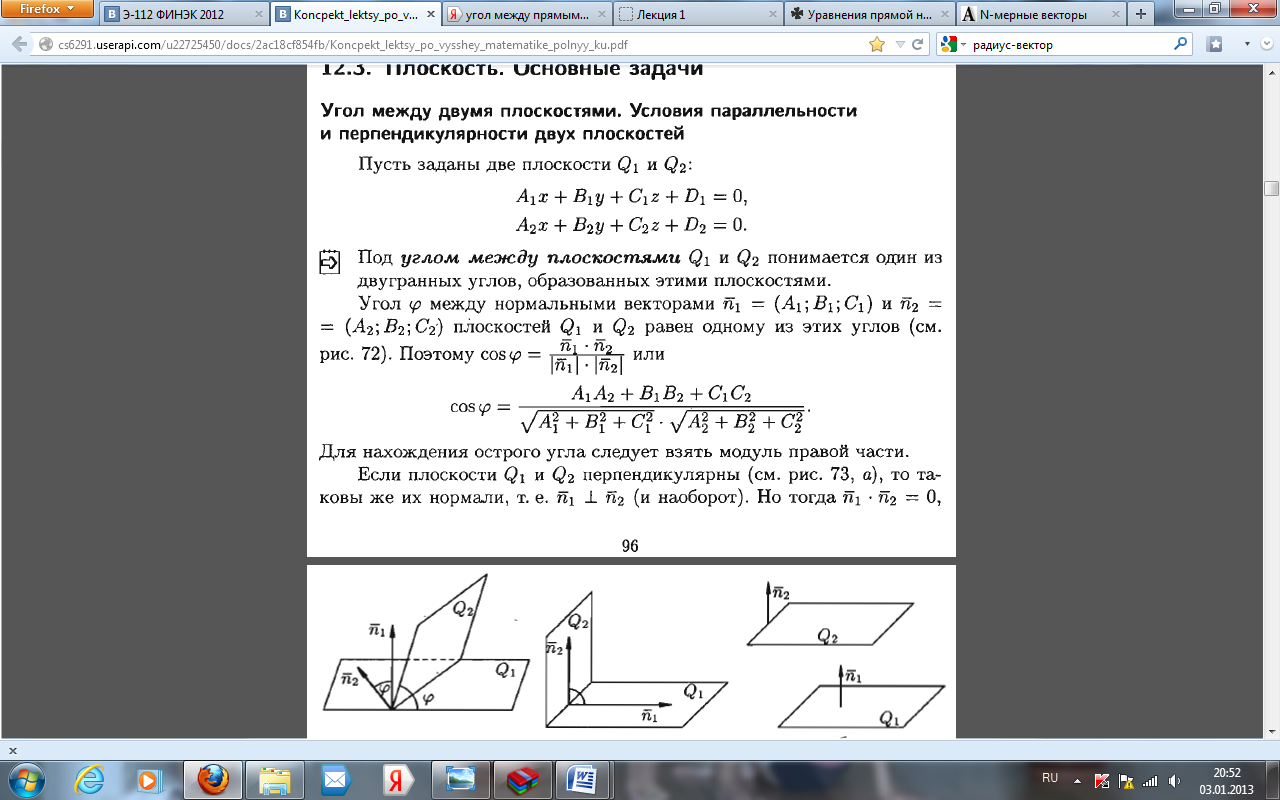
Доказывается, что этот угол не зависит от выбора такой плоскости. Угол между двумя параллельными плоскостями принимается равным нулю.
Две
плоскости α1 и α2 параллельны тогда и
только тогда, когда их нормальные векторы
n1
иn2
параллельны, а значит
![]()
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
![]()
Ясно,
что две плоскости перпендикулярны тогда
и только тогда, когда их нормальные
векторы перпендикулярны, а следовательно,![]() или
или
![]()
