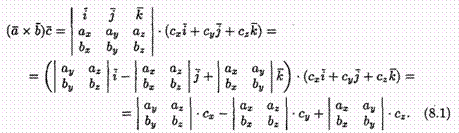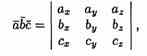- •1.Декартова и полярная системы координат на плоскости. Формулы,связующие координаты точки в этих системах. Декартова система координат в пространстве.
- •2.Понятие геометрического вектора. Основные определения связанные с этим понятием (длина вектора, равенство векторов, нуль-вектор, коллинеарные и компланарные векторы, орт вектора).
- •3.Линейниые операции с геометрическими векторами. Законы, которым удовлетворяют эти операции. Разность векторов. Коллинеарные векторы.
- •4.Деление отрезка в заданном отношении.
- •5. Понятие радиус-вектора. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве.
- •6.Действия с геометрическими векторами в координатной форме.Признак коллинеарности векторов.
- •7.Скалярное произведение геометрических векторов и его свойства. Признак ортогональности векторов.
- •8.Вычисление скалярного произведения векторов через их координаты, длина вектора, расстояние между двумя точками. Вычисление косинуса угла между двумя точками.
- •9. Направляющие косинусы вектора и их свойства.
- •10.Векторное произведение: определение ,вычисление и свойства.
- •11. Смешанное произведение: определение, вычисление, геометрический смысл.
- •12. Общее уравнение прямой на плоскости и его исследование.
- •13. Уравнение прямой с угловым коэффициентом. Геометрический смысл коэффициентов. Пучок прямых
- •18.Различные виды уравнений прямой в пространстве ( каноническое, параметрическое, общее уравнение прямой).
- •19.Условия параллельности и перпендикулярности прямых в пространстве.
- •20. Условия параллельности и перпендикулярности плоскости и прямой в пространстве.
- •21.Угол между прямой и плоскостью.
- •22.Окружность и ее уравнение.
- •23.Определение эллипса и его каноническое уравнение.
- •24. Определение гиперболы и ее каноническое уравнение.
- •25.Определение параболы и ее каноническое уравнение.
- •27.Действия с матрицами (сложение, умножение на скаляр, перемножение матриц, транспонирование матриц). Законы, которым эти действия удовлетворяют.
- •28. Определение определителя и его свойства.
- •29.Определитель, минор и алгебраическое дополнение элемента определителя.
- •30.Обратная матрица. Теорема о существовании и единственности обратной матрицы.Способы вычисления обратной матрицы.
- •3) Способы вычисления обратной матрицы:
- •А) Метод Гаусса—Жордана
- •Б) с помощью матрицы алгебраических дополнений
- •В) Методы Шульца
- •31. Определение ранга матрицы. Базисный минор. Вычисление ранга матрицы с помощью элементарных преобразований.
- •3) Вычисление ранга матрицы с помощью элементарных преобразований.
- •32)Система линейных уравнений и её решение. Различные формы записи линейных уравнений. Определение однородной, неоднородной, совместной, несовместной, определённой и неопределённой систем.
- •А) Векторная форма записи
- •Б) Матричная форма записи
- •33)Матричный способ решения систем линейных уравнений. Пример решения неоднородной слау
- •34) Формулы Крамера.
- •35) Теоре́ма Кро́некера — Капе́лли
- •36)Условия определённости и неопределённости систем линейных уравнений
- •37)Решение систем линейных уравнений метод Гаусса
- •38)Теорема о совместимости однородной системы линейных уравнений
- •39)Теорема о существовании ненулевых решений однородных линейных уравнений.
- •40)Линейное векторное пространство. Пространство r и линейные операции в этом пространстве.
- •41) Скалярное произведение n-мерных векторов. Неравенство Коши-Буняковского
- •42)Определение линейно зависимых и независимых векторов. Критерий линейной зависимости и не зависимости веторов в
- •2) Критерий линейной зависимости векторов
- •43) Базис линейного пространства. Примеры базисов в
- •44. Теорема о единственности разложении вектора линейного пространства по базису.
- •45.Подпространство линейного пространства. Линейная оболочка системы векторов. Сумма и пересечение подпространств. Примеры подпространств.
- •46.Собственные числа и собственные векторы квадратной матрицы и их свойства.
- •47.Характерестическое уравнение , соответствующие квадратной матрице . Теорема о связи собственных чисел матрицы с корнями этого уравнения.
- •48. Линейные операторы. Основные понятия.
- •49. Комплексные числа в алгебраической форме записи .Геометрическое изображение комплексных чисел. Действия с комплексными числами в алгебраической форме записи .Решение алгебраических уравнений
- •50.Тригонометрическая и показательная форма записи комплексных чисел.Модуль и аргумент комплексного числа. Формула Эйлера.
- •51. Действия с комплексными числами. Формула Муавра
- •52)Линейная балансовая модель
- •53) Квадратные формы. Критерий Сильвестра
- •Определение
- •Связанные определения
- •Свойства
- •Критерий положительной определённости квадратичной формы
- •Критерий отрицательной определённости квадратичной формы
9. Направляющие косинусы вектора и их свойства.
Направление вектора в пространстве определяется углами , которые вектор образует с осями координат. Косинусы этих углов называются направляющими косинусами вектора: соsa,cosbB,cos∂.
![]() ,
,
![]() ,
,![]() ,
из этого
следует :
,
из этого
следует :
![]() ,
,![]() ,
,
![]()
Свойства:

координаты любого единичного вектора совпадают с его направляющими косинусами:
![]()
10.Векторное произведение: определение ,вычисление и свойства.
Три некомпланарных вектора a,bи с, в указанном порядке образуют правую тройку, если с конца третьего вектора с кратчайший поворот от первого вектора а ко второму совершается против часовой стрелки, и левую если по часовой.

Векторным произведением вектора а на вектор b называется вектор с, который:
перпендикулярен векторам а и b
имеет длину, численно равную площади параллелограмма , построенного на векторах а и b, как на сторонах. С= |а|*|b|*sin(a^b)

векторы a,b,cобразуют правую тройку.
Векторное произведение обозначается а *b
Из определения векторного произведения вытекает следующее соотношение между ортами I,j,k: i*j=k, j*k=I, k*i=j.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак. a*b=-(b*a)
Векторное произведение обладает сочетательным свойством относительно скалярного множителя ,т.е лямбда(a*b)= (лямбда*a)*b=a*(лямбда*b)
Два ненулевых вектора а и b коллинеарны тогда и только тогда, когда их векторное произведение равно нулевому вектору. a//b ↔ a*b=0
Распределительное свойство : (a+b)*c= a*c+b*c
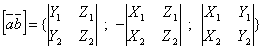 ,
,
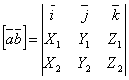
11. Смешанное произведение: определение, вычисление, геометрический смысл.
Определение
смешанного произведения и его
геометрический смысл.
Первые два вектора перемножаются
векторно, а их результат скалярно на
третий вектор. Такое произведение
называется векторно-скалярным или
смешанным. Смешанное произведение
представляет собой число. Смешанное
произведение трех векторов, равно объему
параллелепипеда, построенного на этих
векторах , взятого со знаком плюс, если
эти векторы образуют правую тройку, и
со знаком минус если образуют
 левую
тройку.
левую
тройку.
Имеем: (а х b) • с = d • с = |d| • прdс, |d|=|а х b| =S, где S — площадь параллелограмма, построенного на векторах а и b, прdс = Н Для правой тройки векторов и прdс = - Н для левой, где Н— высота параллелепипеда. Получаем: (axb )*c =S *(±H ), т. е. (axb )*c =±V , где V — объем параллелепипеда, образованного векторами а, b и с.
Свойства:
Смешанное произведение не меняется при циклической перестановке его сомножителей. (a*b)*c=(b*c)*a=(c*a)*b
Смешанное произведение не меняется при перемене местами знаков вектарного и скалярного умножения. (a*b)*c=a*(b*c)
Смешанное произведение меняет свой знак при перемене мест любых двух векторов-сомножителей. abc=-acb; abc=-bac; abc=-cba
Смешанное произведение ненулевых векторов a,bи с равно нулю тогда и только тогда , когда они компланарны.
Смешанное произведение векторов равно определителю третьего порядка, составленному из координат перемножаемых векторов.