53) Квадратные формы. Критерий Сильвестра
1)Квадратичная форма — функция на векторном пространстве, задаваемая однородным многочленом второй степени от координат вектора.
Определение
Пусть
есть
векторное
пространство
над полем
и
—
базис в
.
Функция
называется
квадратичной формой, если её можно
представить в виде
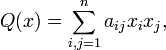
где
,
а
—
некоторые элементы поля
.
Связанные определения
Матрицу
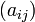называют
матрицей квадратичной формы в данном
базисе. В случае, если характеристика
поля
не
равна 2, можно считать, что матрица
квадратичной формы симметрична, то
есть
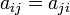.Для любой квадратичной формы
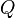существует
единственная симметричная билинейная
форма
,
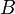такая, что
.
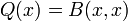Билинейную форму
называют
полярной
к
,
она может быть вычислена по формуле
Матрица квадратичной формы в произвольном базисе совпадает с матрицей полярной ей билинейной формы в том же базисе.
Если матрица квадратичной формы имеет полный ранг, то квадратичную форму называют невырожденной, иначе — вырожденной.
Свойства
Критерий Сильвестра
Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны.
Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен.
Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения.
Для любой невырожденной квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
Разность между числом положительных (
)
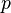и отрицательных (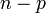
)
членов в этой записи называется
сигнатурой
квадратичной формы. Сигнатура, также
как и числа положительных и отрицательных
слагаемых, не зависят от способов
приведения квадратичной формы к
каноническому виду (закон
инерции Сильвестра).Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа.
2) Критерий Сильвестра определяет, является ли симметричная квадратная матрица положительно (отрицательно, неотрицательно) определённой.
Пусть квадратичная форма имеет в каком-то базисе матрицу
Тогда
эта форма положительно определена,
тогда и только тогда когда все её главные
(угловые) миноры
положительны.
Форма отрицательно определена, если и
только если знаки
чередуются,
причём
.
Критерий положительной определённости квадратичной формы
-
Для положительной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры её матрицы были положительны.
Критерий отрицательной определённости квадратичной формы
-
Для отрицательной определённости квадратичной формы необходимо и достаточно, чтобы главные миноры чётного порядка её матрицы были положительны, а нечётного порядка — отрицательны.