47.Характерестическое уравнение , соответствующие квадратной матрице . Теорема о связи собственных чисел матрицы с корнями этого уравнения.
- характеристическое
уравнение матрицы А.
В квадратной матрице порядка :
число корней характеристического уравнения, отличных от нуля, равно рангу матрицы, т. е. ранг матрицы меньшеn тогда и только тогда, когда по крайней мере один корень характеристического уравнения равен нулю;
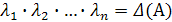
если матрица симметричная, то все n корней характеристического уравнения действительные
Собственными числами матрицы А являются корни уравнения и только они.
48. Линейные операторы. Основные понятия.
Оператором называется правило, по которому каждому элементу x некоторого непустого множества X ставится в соответствие единственный элемент y некоторого непустого множества Y. Говорят, что оператор действует из X в Y.
Действие оператора обозначают y = A(x), y — образ x, x — прообраз y.
Если каждый элемнт y из Y имеет единственный прообраз x из X, y= A(x), оператор называют взаимно однозначным отображением X в Y или преобразованием X, X — область определения оператора.
Пусть X и Y два линейные пространства. Оператор A, действующий из X в Y, называется линейным оператором, если для любых двух элементов u и v из X и любого числа α справедливо:
A(u + v) = A(u ) + A(v) , A(α·u) = α· A(u).
49. Комплексные числа в алгебраической форме записи .Геометрическое изображение комплексных чисел. Действия с комплексными числами в алгебраической форме записи .Решение алгебраических уравнений
Ко́мпле́ксные чи́сла (устар. Мнимые числа), — расширение множества вещественных чисел, обычно обозначается С. Любое комплексное число может быть представлено как формальная сумма x + iy, где x и y — вещественные числа, i — мнимая единица
Поле комплексных чисел можно понимать как расширение поля вещественных чисел, в котором многочлен z2 + 1 имеет корень. Следующие две элементарные модели показывают, что непротиворечивое построение такой системы чисел возможно. Оба приведенных определения приводят к изоморфным расширениям поля вещественных чиселR, как и любые другие конструкции поля разложения многочлена z2 + 1.
Запись комплексного
числа z
в виде x
+ iy,
,называется алгебраической формой
комплексного числа.
Сумма и произведение комплексных чисел могут быть вычислены непосредственным суммированием и перемножением таких выражений, как обычно раскрывая скобки и приводя подобные, чтобы представить результат тоже в стандартной форме (при этом надо учесть, что i2 = − 1):
(a + ib) +
(c + id) = (a + c) + i(b + d);
Рассмотрим плоскость
с прямоугольной системой координат.
Каждому комплексному числу
сопоставим точку плоскости с координатами
{x,y}
(а также радиус-вектор, соединяющий
начало координат с этой точкой). Такая
плоскость называется комплексной.
Вещественные числа на ней занимают
горизонтальную ось, мнимая единица
изображается единицей на вертикальной
оси; по этой причине горизонтальная и
вертикальная оси называются соответственно
вещественной и мнимой осями.
Часто бывает удобно рассматривать на комплексной плоскости также полярную систему координат, в которой координатами точки являются расстояние до начала координат (модуль) и угол радиус-вектора точки (показанного синей стрелкой на рисунке) с горизонтальной осью (аргумент).
Действия над комплексными числами
Сравнение
a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение
(a + bi) + (c + di) = (a + c) + (b + d)i.
Вычитание
(a + bi) − (c + di) = (a − c) + (b − d)i.
