36)Условия определённости и неопределённости систем линейных уравнений

Теорема: Если ранг основной матрицы совместной системы равен числу неизвестных, то система является определённой

Теорема: Если ранг основной матрицы совместной системы меньше числа неизвестных, то система является неопределённой.

37)Решение систем линейных уравнений метод Гаусса

Для того чтобы решить систему уравнений

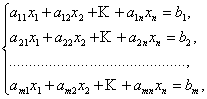  выписывают расширенную матрицу этой системы 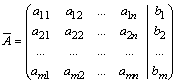и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы  будут располагаться нули. Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число. С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы.

38)Теорема о совместимости однородной системы линейных уравнений

. Если свободные члены системы линейных уравнений равны 0, то система однородна.

a ₁₁ x₁ + a₁₂ x₂+…+a_1nx=0

a₂₁x₁+a₂₂x₂+…+a_2nx_n=0

………………………………….

a_m1x₁₊a_m2x₂+…+a_mnx_n=0

Однородная система всегда совместна, т. к. набор чисел 0.0..0.всегда является решением системы, такое решение называется тревиальным.

39)Теорема о существовании ненулевых решений однородных линейных уравнений.

Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n  неизвестных, т. е. r<n.  

Необходимость.

Так как ранг не может превосходить размера матрицы, то, очевидно, r<=n. Пусть r=n. Тогда один из минеров размера nхn отличен от нуля. Поэтому соответствующая система линейных уравнений имеет единственное решение:

 

Значит, других, кроме тривиальных, решений нет. Итак, если есть нетривиальное решение, то r<n.

Достаточность:

Пусть r<n. Тогда однородная система, будучи совместной, является неопределенной. Значит, она имеет бесчисленное множество решений, т. е. имеет и ненулевые решения. Пусть дана однородная система n линейных уравнений с n неизвестными

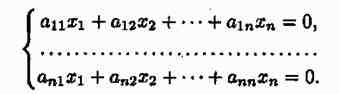
Для того, чтобы система однородных уравнений имела ненулевые решения, необходимо и достаточно, чтобы ранг r ее основной матрицы был меньше числа n неизвестных, т. е. r

Для того, чтобы однородная система n линейных уравнений с n неизвестными имела ненулевые решения, необходимо и достаточно, чтобы ее определитель D был равен нулю, т. е. D=0.

40)Линейное векторное пространство. Пространство r и линейные операции в этом пространстве.

Векторное (линейное) пространство — это математическая структура, которая формируется набором элементов, называемых векторами, для которых определены операции сложения друг с другом и умножения на число — скаляр. Введённые операции подчинены восьми аксиомам. Скаляром же может являться элемент вещественного, комплексного или любого другого поля чисел. Частным случаем векторов подобного пространства являются обычные евклидовы вектора, которые используются, к примеру, для демонстрации физических сил. При этом следует отметить, что вектор как элемент векторного пространства не обязательно должен быть представлен в качестве направленного отрезка. Обобщение понятия «вектор» до элемента векторного пространства любой природы не только не вызывает смешения терминов, но и позволяет уяснить или даже предвидеть ряд результатов, справедливых для пространств произвольной природы.

Свойства:

1. Векторное пространство является абелевой группой по сложению.

2. Нейтральный элемент 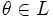является единственным, что вытекает из групповых свойств.

3. для любого .

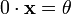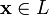4. Для любого противоположный элемент 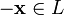является единственным, что вытекает из групповых свойств.

5. для любого .

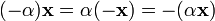6. для любых 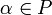и .

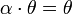7. для любого .

Для любых векторов x, y и z из Rn и любых чисел α и β справедливо:

1. x + y = x + y, сложение коммутативно;

2. x + (y + z) = (x + y)+ z, сложение ассоциативно;

3. x + θ = x;

4. x + (−x) = θ;

5. α(x + y) = αx + αy, умножение на число дистрибутивно относительно сложения векторов;

6. α(βx) = (αβ)x, умножение на число ассоциативно;

7. (α + β)x = αx + βx , умножение вектора на число дистрибутивно относительно сложения чисел.

8. 1·x = x.

Пространство Rn − n-мерное векторное пространство, dimRn = n.

Если в пространстве Rn определен естественный базис e₁, e₂, ... e_n ,

e₁= (1, 0, 0,..., 0, 0), e₂= (0, 1, 0,..., 0, 0), ..., e_n-1= (0, 0, 0,..., 1, 0), e_n= (0, 0, 0,..., 0, 1),

то компоненты вектора x = (x₁, x₂, ..., x_n) из Rn являются координатами вектора x в естественном базисе e₁, e₂, ... e_n:

x = (x₁, x₂, ..., x_n) = x₁e₁+ x₂e₂+ ...+ x_ne_n.

 Арифметическим вектором называется упорядоченная совокупность n чисел.

Обозначается x = (x₁, x₂, ..., x_n);

числа x₁, x₂, ..., x_n называются компонентами арифметического вектора.

Для арифметических векторов определены линейные операции — сложение арифметических векторов и умножение вектора на число:

для любых x = (x₁, x₂, ..., x_n), y = (y₁, y₂, ..., y_n) и любого числа α справедливо:

x + y = (x₁+ y₁, x₂ +y₂, ..., x_n+ y_n); αx = (αx₁, αx₂, ..., αx_n).

Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.

Вектор θ = (0, 0, ..., 0) называется нулевым вектором Rn,

а вектор −x = (−x₁, −x₂, ..., −x_n) — противоположным вектором для вектора x в Rn.