Б) Матричная форма записи

В матричной записи система линейных уравнений может быть записана следующим образом:

AX=B

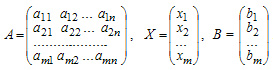
Пример 2: Записать в матричном виде систему из предыдущего примера

3) Если все правые части системы равны нулю, то система называется однородной.

4) Если среди правых частей b_i системы есть хоть одна, отличная от нуля, то система называется неоднородной системой линейных уравнений.

5) Совместной называется система уравнений, если она имеет хотя бы одно решение.

6) Несовместной называется система уравнений, если она не имеет ни одного решения.

7) Определенной называется система уравнений, если она имеет единственное решение.

8) Неопределенной называется система уравнений, если она имеет бесконечное множество решений.

33)Матричный способ решения систем линейных уравнений. Пример решения неоднородной слау

Сначала убедимся в том, что определитель матрицы из коэффициентов при неизвестных СЛАУ не равен нулю.

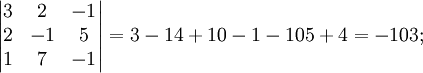Теперь вычислим алгебраические дополнения для элементов матрицы, состоящей из коэффициентов при неизвестных. Они нам понадобятся для нахождения обратной матрицы.

Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

Далее найдём союзную матрицу, транспонируем её и подставим в формулу для нахождения обратной матрицы.

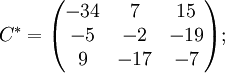
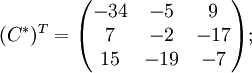
Подставляя переменные в формулу, получаем:

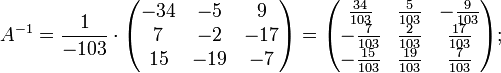
Осталось найти неизвестные. Для этого перемножим обратную матрицу и столбец свободных членов.

Итак, x=2; y=1; z=4.

34) Формулы Крамера.

Метод Крамера (правило Крамера) — способ решения квадратных систем линейных алгебраических уравнений с ненулевым определителем основной матрицы

Пример:

Система линейных уравнений:

Определители:

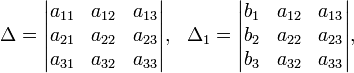
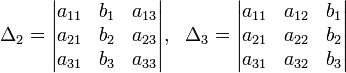
Решение:

35) Теоре́ма Кро́некера — Капе́лли

Теоре́ма Кро́некера — Капе́лли — критерий совместности системы линейных алгебраических уравнений:

алгебраических уравнений:

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Для того чтобы линейная система являлась совместной, необходимо и достаточно, что бы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.

Доказательство (условия совместности системы)

Необходимость

Пусть система совместна. Тогда существуют числа такие, что . Следовательно, столбец является линейной комбинацией столбцов матрицы . Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что .

Достаточность

Пусть . Возьмем в матрице какой-нибудь базисный минор. Так как , то он же и будет базисным минором и матрицы . Тогда согласно теореме о базисном миноре последний столбец матрицы будет линейной комбинацией базисных столбцов, то есть столбцов матрицы . Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы .

Следствия

• Количество главных переменных системы равно рангу системы.

• Совместная система будет определена (её решение единстве