6) Силы и потенциальная энергия межмолекулярного взаимодействия. Реальные газы. Уравнение Ван-дер-Ваальса. Изотермы реального газа. Критическое состояние вещества. Внутренняя энергия реального газа.

Ван-дер-Ваальсовы силы — силы межмолекулярного (и межатомного) взаимодействия с энергией 10 — 20 кДж/моль. Этим термином первоначально обозначались все такие силы, в современной науке он обычно применяется к силам, возникающим при поляризации молекул и образовании диполей. Открыты Я. Д. ван дер Ваальсом в 1869 году.

Ван-дер-ваальсовое взаимодействие состоит из трех типов слабых взаимодействий:

• Ориентационные силы, диполь-дипольное притяжение. Осуществляется между молекулами, являющимися постоянными диполями. Примером может служить HCl в жидком и твердом состоянии. Энергия такого взаимодействия обратно пропорциональна шестой степени расстояния между диполями.

• Дисперсионное притяжение (лондоновские силы). Взаимодействием между мгновенным и наведенным диполем. Энергия такого взаимодействия обратно пропорциональна шестой степени расстояния между диполями.

• Индукционное притяжение. Взаимодействие между постоянным диполем и наведенным (индуцированным). Энергия такого взаимодействия обратно пропорциональна шестой степени расстояния между диполями.

Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева.

Состояние реального газа часто на практике описывается обобщённым уравнением Менделеева — Клапейрона:

где p — давление; V - объем T — температура; Z_r = Z_r (p,T)  — коэффициент сжимаемости газа; m - масса; М — молярная масса; R — газовая постоянная.

Уравнение состояния газа Ван-дер-Ваальса — уравнение, связывающее основные термодинамические величины в модели газа Ван-дер-Ваальса.

Хотя модель идеального газа хорошо описывает поведение реальных газов при низких давлениях и высоких температурах, в других условиях её соответствие сопытом гораздо хуже. В частности, это проявляется в том, что реальные газы могут быть переведены в жидкое и даже в твёрдое состояние, а идеальные — не могут.

Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия   становится функцией не только температуры, но и объёма.

Уравнение Ван-дер-Ваальса — это одно из широко известных приближённых уравнений состояния, имеющее компактную форму и учитывающее основные характеристики газа с межмолекулярным взаимодействием^[1].

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

где

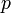•  — давление,

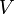•  — молярный объём,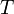

•  — абсолютная температура,

•  — универсальная газовая постоянная.

Критическое состояние – состояние, при котором исчезает различие между жидкостью и газом. А температура, при которой система находится в критическом состояний, называют критической.

Внутренняя энергия реального газа будем определяться суммой кинетической энергии E_к теплового движения его молекул и потенциальной энергии взаимодействия молекул между собой - E_п: 

U=E_к+E_п.

U_m=C_vT-(a/V_m)

Из формулы для внутренней энергии реального газа следует, что его внутренняя энергия растет как с увеличением температуры, так и с увеличением объема. Если реальный газ будет расширяться или сжиматься адиабатически и без совершения внешней работы, то для него, согласно первому началу термодинамики: 

ΔQ=ΔU+ΔA; ΔQ=0, ΔA=0; ⇒ ΔU=0 → U=const,