3. Регулирование частоты вращения ведомого вала.
С изменением частоты вращения изменяется и вращающий момент: меньшей частоте соответствует больший момент (при трогании автомобиля с места, при съеме стружки большой толщины). Для регулирования частоты вращения ведомого вала применяют коробки передач и вариаторы. Коробки передач обеспечивают ступенчатое изменение частоты вращения ведомого вала, вариаторы – бесступенчатое).
Преобразование одного вида движения в другой (вращательного в поступательное, равномерного в прерывистое и т.Д.).
Реверсирование движения (прямой и обратный ход).
Распределение энергии двигателя между несколькими исполнительными элементами машины.
Классификация передачВ самом общем виде передачи можно классифицировать по способу передачи движения:передачи трением (фрикционные, ременные); передачи зацеплением (зубчатые, червячные, цепные, винт—гайка); по способу соединения звеньев: передачи с непосредственным контактом (фрикционные, зубчатые, червячные, винт—гайка); передачи гибкой связью (ременные, цепные).
Звено передачи, которое получает движение от машины-двигателя, называется ведущим; звено, которому передается движение, называется ведомым; кроме того, в передачах бывают промежуточные звенья.
Н
а
рис. схематически изображены передача
гибкой связью (а)и передача
с непосредственным контактом (б),причем
индексом 1обозначены
параметры, относящиеся к ведущему
звену, а индексом 2 – к
ведомому. Обратим внимание на то, что
в первой из изображенных передач
направление
вращения ведущего и ведомого звеньев
совпадают, а во второй
— изменяется на противоположное.
Основные характеристики передач: передаточное число, передаваемая мощность и КПД.
Передаточным отношением называется отношение угловой скорости ведущего звена к угловой скорости ведомого звена. Обозначается буквой i.Передаточное отношение может быть больше, меньше или равно единице.
30.
В зубчатой передаче движение передают с помощью зацепления пары зубчатых колес. Меньшее зубчатое колесо принято называть шестерней, большее — колесом. Термин "зубчатое колесо" относят как к шестерне, так и к колесу.
Достоинства зубчатых передач:
1.Относительно малые размеры и масса зубчатых колес при высокой нагрузочной способности и надежности.
2.Высокий КПД (97 - 98 %).
3.Возможность использования зубчатых передач в большом диапазоне нагрузок (окружные силы от близких к нулю в приборных механизмах до —1000 кН в приводах прокатных станов).
4.Возможность применения в широком диапазоне скоростей (окружные скорости от близких к нулю в системах перемещения телескопов до 250 м/св приводе несущего винта, вертолета).
5Сравнительно малые нагрузки на валы и подшипники.
6.Постоянство среднего значения передаточного числа.
7.Простота обслуживания.
Недостатки:
1. Необходимость высокой точности изготовления и монтажа.
2. Шум при работе передачи. Шум обусловлен переменным значением мгновенного передаточного числа в пределах одного Зубчатые передачи можно классифицировать по многим признакам, а именно: по расположению осей валов(с параллельными, пересекающимися, скрещивающимися осями и соосные); по условиям работы(закрытые — работающие в масляной ванне и открытые — работающие всухую или смазываемые периодически); по числу ступеней(одноступенчатые, многоступенчатые); по взаимному расположению колес(с внешним и внутренним зацеплением); по изменению частоты вращения валов(понижающие, повышающие); по форме поверхности, на которой нарезаны зубья (цилиндрические, конические); по окружной скоростиколес (тихоходные при скорости до 3 м/с); среднескоростные при скорости до 15 м/с, быстроходные при скорости выше 15 м/с); по расположению зубьевотносительно образующей колеса (прямозубые, косозубые, шевронные, с криволинейными зубьями); по форме профиля зуба(эвольвентные, круговые, циклоидальные).
31.
влияние числа зубьев на форму и прочность зубьев
С уменьшением z уменьшается толщина зуба у основания и вершины, а также увеличивается кривизна эвольвентного профиля. Такое изменение формы приводит к уменьшению прочности зуба. При дальнейшем уменьшении z появляется подрезание ножки зуба, прочность зуба существенно снижается. При нарезании инструментом реечного типа для прямозубых передач число зубьев на границе подрезания
32.
Основными ошибками изготовления зубчатых колес являются: ошибка шагаи формы профиля зубьев, ошибка в направлении зубьев относительно
образующей делительного цилиндра.
О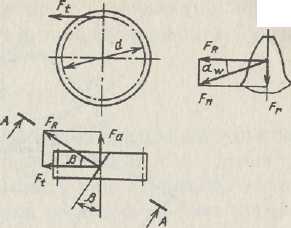
шибка
шага и профиля нарушает кинематическую
точность и плавностьработы передачи.
В передаче сохраняется постоянным
только среднее значениепередаточного
отношения i. Мгновенные значения i в
процессе вращения
меняются.
Колебания передаточного отношения особенно нежелательны вкинематических цепях, выполняющих следящие, делительные и измерительныефункции. В силовых быстроходных передачах с ошибками шага и профилясвязаны дополнительные динамические нагрузки, удары и шум в зацеплении.
Ошибки в направлении зубьев в сочетании с перекосом валов вызываютнеравномерное распределение нагрузки по длине зуба.
Точность изготовления зубчатых передач регламентируется стандартом(СТ СЭВ 641–77), который предусматривает 12 степеней точности. Каждаястепень точности характеризуется тремя показателями:
1) нормойкинематической точности, регламентирующей наибольшую погрешностьпередаточного отношения или полную погрешность угла поворота зубчатогоколеса в пределах одного оборота (в зацеплении с эталонным колесом); 2) нормой
плавности работы, регламентирующей многократно повторяющиесяциклические ошибки передаточного отношения или угла поворота в пределаходного оборота; 3) нормой контакта зубьев, регламентирующей ошибкиизготовления зубьев и сборки передачи, влияющие на размеры пятна контакта взацеплении (распределение нагрузки по длине зуба).
Степень точности выбирают в зависимости от назначения и условий работыпередачи, в первую очередь в зависимости от окружной скорости. Наибольшеераспространение имеют 6, 7, 8 и 9 степени точностио избежание заклинивания зубьев в зацеплении должен быть боковойзазор. Размер зазора регламентируется видом сопряжения зубчатых колес.Согласно ГОСТ 1643–81 устанавливается шесть видов сопряжений, обозначаемых
Таблица 3.2
Окружная скорость, м/с, не
Степень
более Область применения
точности
прямозубая косозубая
6 Высокоскоростные передачи, механизмы
(высоко- 15 30 точной кинематической связи, отсчетные и
точные) др.
Передачи при повышенных скоростях и
7
10 15 умеренных нагрузках или при повышенных
(точные)
нагрузках и умеренных скоростях.
8
Передачи общего машиностроения, не
(средней 6 10
требующие особой точности.
точности)
9
Тихоходные передачи с пониженными
(пониженно 2 4
требованиями к точности.
й точности)
А, В, С, D, Е, Н, при которых реализуются по величине гарантированные зазоры,
и восемь допусков на боковой зазор: x, y, z, a, b, c, d, h. Обозначения даны в
порядке убывания величины гарантированного зазора и допуска на зазор. Здесь x,
y, z –дополнительные допуски.
Поскольку величина бокового зазора зависит от изменения межосевого
расстояния, ГОСТ 1643-81 устанавливает шесть классов отклонений межосевого
расстояния, обозначаемых в порядке убывания точности цифрами от I до VI.
Например, для сопряжений H и E соответствует II класс точности межосевого
расстояния.
33.
Силы взаимодействия зубьев принято определять в полюсе за¬цепления. Распределенную по контактной площадке нагрузку q в зацеплении заменяют равнодействующей Fn, нормальной к поверх¬ности зуба.
А-А О
Для расчета валов и опор силу Fn удобно представить в виде составляющих (рис. 15.1): Ft , FaFr
Окружная сила:
Ft
= 2.∙103 T/d, осевая сила:
Рис. 15.1
На ведомом колесе направ¬ление окружной силы Ft, совпа-дает с направлением вращения, на ведущем - противоположно ему.
Осевая сила параллельна оси колеса. Направление вектора Fa зависит от направления вращения колеса и направления линии зуба.
Для определения радиальной силы Fr запишем промежуточное выражение
FR = Ft/cosβ. Тогда радиальная сила (см. сечение А-А)
ЗДЕСЬ Т - вращающий момент на зубчатом колесе, Нм; d - де-лительный диаметр колеса, мм; β- угол наклона зуба; αw = 20 ° -угол зацепления.
Векторы радиальных сил у колес с внешним зацеплением на-правлены к оси, а у колес с внутренним зацеплением - от оси зубча¬того колеса.
34.
Контактные
напряжения возникают при взаимодействии
тел,
размеры площадки контакта
которых малы по сравнению с размера-
ми
самих соприкасающихся тел,
например, контакт двух стальных
круговых
цилиндров по общейобразующей,
рис.6 (аналог
зубчатого зацепления,
фрик-ционной передачи,
ролико-вых подшипников), контакт шара
и тора (шариковые
подшипники
качения).Контакт
при перекатывании
Р Рис.6
в передачах и опорах
качения происходит
по малым площадкам (начальный контакт
по линии или в точке),
вследствие чего в поверхностном слое
возникают высокие напряжения.
Материал в районе этой площадки
испытывает объемное напряженное
состояние. Впервые исследованием
контактных напряжений занимался
физик Герц (допускается одно из написаний
Hertz
или Herz).
В его честь контактные напряжения
обозначают с индексом Н:
σН.
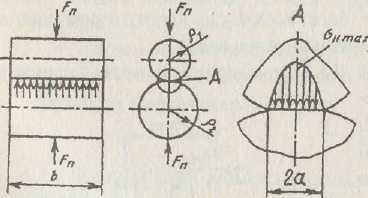
Контакт ненагруженных прижимающей силой цилиндров с параллельными осями происходит по линии (по образующей). Под действием прижимающей силы Fn, вследствие упругих деформаций цилиндров первоначальный контакт по линии переходит в контакт по прямоугольной площадке (очень узкой полоске) шириной 2а. Размеры площадки контакта и возникающие нормальные напряжения σНзависят от нагрузки Fn, упругих характеристик материалов (коэффициентов Пуассона, модулей упругости) и формы контактирующих тел. Как показывают исследования, в поперечном сечении по площадке контакта напряжения изменяются по эллиптическому закону, достигая максимального значения аятах в зоне максимальных деформаций - по линии действия прижимающей силы (выносной элемент А).Особенностью действия нормальных контактных напряжений является то, что они не распространяются глубоко в тело деталей, сосредотачиваясь в тонком поверхностном слое.
Кроме нормального напряжения σН в зоне контакта возникают также касательные напряжения τ. Наибольшее касательное напряжение τmах = 0,3σНmах имеет место в точке, расположенной на линии действия прижимающей силы Fnи отстоящей от поверхности соприкосновения на 0,78а.
Числовые значения контактных напряжений намного превышают как значения других видов напряжений (растяжения, изгиба), так и механических характеристик материала при одноосном напряженном состоянии: σт и σв. Так, в подшипниках качения σНmах= 4600 МПа, в то время как для применяемой стали марки ШХ15 предел текучести σт = 1700 МПа, временное сопротивление σв= 1900 МПа. Отсутствие мгновенного разрушения при наличии столь высоких напряжений объясняют тем, что в зоне их действия материал находится в условиях всестороннего объемного сжатия.
Максимальное значение σНmах используют в качестве основного критерия контактной прочности:
где [σ]Н - допускаемое контактное напряжение, полученное из эксперимента или опыта эксплуатации при аналогичных условиях в зоне контакта.
Для вычисления максимального контактного напряжения на площадке контакта используют формулу Герца, полученную из ре-
шения контактной задачи теории упругости (индекс "max" при этом
опускают):
35.
1. Поломка зуба, обусловленная многократно повторяющимися нагрузками, вызывает усталость его материала. Такое разрушение является наиболее опасным видом потери работоспособного состояния, приводящим к внезапному выходу из строя передачи. Трещины обычно появляются у корня зуба на стороне растянутых волокон. Условие объемной усталостной прочности имеет следующий вид:
.
2. Усталостноевыкрашивание поверхностного слоя зубьев является наиболее распространенным видом повреждения закрытых передач. Усталостные трещины обычно зарождаются у поверхности, где возникает концентрация напряжения из-за микронеровностей.
Условием контактной усталостной прочности является
.
3. Поломку зубьев могут вызвать большие пиковые нагрузки. В этом случае условие объемной статической прочности записывают в виде
.
4. Пластические деформации поверхностей зубьев может вызваться большими перегрузками. Условия контактной статической прочности имеет вид
37.
Вторым из двух основных критериев работоспособности зуб¬чатых передач является прочность зубьев при изгибе. При выводе расчетной зависимости принимают допущения (рис. 15.3):
1. В зацеплении находится одна пара зубьев.
2. Зуб рассматривают как консольную балку, нагруженную со¬-
средоточенной силой Fn, приложенной к зубу в его вершине.
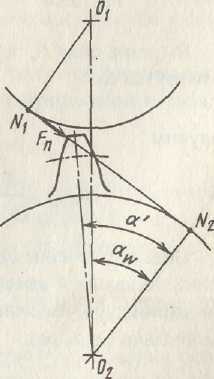
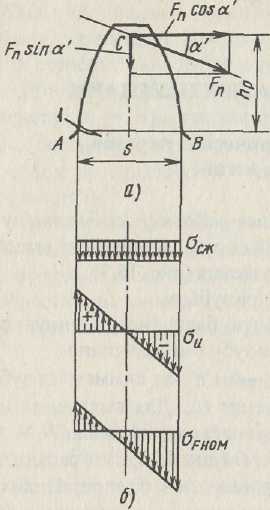
Сила Fn действует под углом (90° - α') к оси симметрии зуба; угол α' несколько больше угла зацепления αw. Для выявления на¬пряженного состояния зуба силу Fn переносят вдоль линии N1N2 за¬цепления до пересечения с осью зуба в т. С (рис. 15.4, а) и расклады¬вают на составляющие, направленные вдоль оси зуба и перпендику¬лярно ей.
Под
действием составляющей, направленной
вдоль оси, в основании зуба действуют
напряжения сжатия
σсж = Fnsinα'/(bS), эпюра которыхпо¬казана на рис. 15.4, б. Здесь b - длина зуба.
Точки А и В определяют положе¬ние опасного сечения зуба при изгибе. Зуб в этом сечении нагружен изги¬бающим моментом М = Fnhpcosα',
вызывающим действие напряжений σи: слева от оси по рис. 15.4, б — рас¬тяжения, справа - сжатия.
Суммарные напряжения σFHOM со стороны растянутых волокон (т. А) имеют меньшие значения, чем со стороны сжатых (т. В). Однако напряжения растяжения являются более опасными. Как
показывает опыт эксплуатации, усталостная трещина 1, приводящая к выламыванию зуба, зарождается именно со стороны рас¬тянутых волокон B T.A (рис. 15.4). Напряжения, найденные без учета концентраторов, называют номи¬нальными.
Определим номинальные напря¬женияσFHOM изгиба-сжатия B T.A:
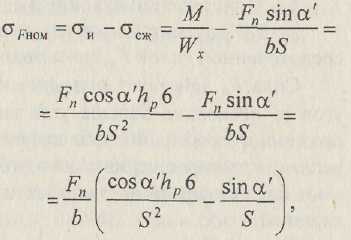
где Wx = bS2/6 - осевой момент сопротивления опасного сечения АВ.
Выразив
силу Fn через окружную силу Ft с учетом
коэффициен¬та нагрузки KF:
Получим
Опасное сечение АВ расположено в зоне концентрации напря¬жений, вызванной изменением формы на переходной поверхности в основании зуба. Местные напряжения в этом сечении превышают номинальные в αт раз:
σF
= σFном αт , где αт - теоретический
коэффициент концентрации напряжений.
Плечо изгиба hp и толщину зуба S выражают через модуль т:
hp = μт и S = λт,
где μ и λ - коэффициенты, учитывающие форму зуба. Тогда
где YFs - коэффициент, учитывающий форму зуба и концентрацию
напряжений:
Значения коэффициента YFs, учитывающего форму зуба и кон¬центрацию напряжений, приведены в литературе в виде таблиц или графиков. Меньшие значения коэффициента YFs соответствуют большему числу зубьев и положительному смещению инструмента, так как и то и другое приводит к увеличению толщины зуба у осно¬вания.
Учитывая условие прочности σF ≤ [σ]F, получим формулу для проверочного расчета зубчатых передач по напряжениям изгиба:
(15.4)
где [σ]F - допускаемые напряжения изгиба, МПа; Ft - в Н; b и m - в мм.
В полученную формулу дополнительно введены: Yβ - коэффи¬циент, учитывающий угол наклона зуба, и Yε - коэффициент, учиты¬вающий перекрытие зубьев.
Для прямозубых зубчатых колес: Yβ = 1; Yε = 1 при степени точ¬ности 8,9; Yε = 0,8 при степени точности 5 - 7.
Из-за меньшего числа зубьев зуб шестерни у основания более тонкий, чем зуб колеса; это отражено в большем значении коэффи¬циентаYFs(YFs1 > YFs2). Для обеспечения примерно равной изгибной
прочности сопряженных зубьев шестерню изготовляют из более прочного по сравнению с колесом материала.
Условие равной прочности на изгиб зубьев шестерни и колеса [σ] F1 /YFs1 ≈ [σ] F2 / YFs2 .
38.
Конические зубчатые передачи применяют для передачи механической энергии между валами с пересекающимися осями. Наибольшее распространение имеют ортогональные (с углом ∑ = 90°) передачи (рис. 16.1). Как отмечалось (см. лекцию 13), конические колеса бывают с прямыми и круговыми зубьями.
Линии зуба в конических колесах с круговыми зубьями являются дугами окружности.
Передачи с прямыми зубьями имеют начальный линейный, а с круговыми зубьями - точечный контакт в зацеплении. Угол βn наклона линии зуба определяют в среднем сечении по ширине зубчатого венца. Для передачи с прямым зубом βn = 0, для передачи с круговым зубом βn = 35°. Наличие наклона линии зуба повышает плавность работы, контактную прочность и прочность на изгиб, но увеличивает нагрузки на опоры и валы. Конические колеса с круговыми зубьями по сравнению с прямозубыми обладают большей несущей способностью, работают плавно и с меньшим шумом.
Для повышения износостойкости и сопротивления зубьев заеданию смещением исходного контура выравнивают удельные скольжения в граничных точках зацепления. Шестерню выполняют с положительным смещением, а колесо с равным ему по абсолютному значению - отрицательным.
Аналогами начальных цилиндров цилиндрических зубчатых передач в конических передачах являются делительные конусы, совпадающие с начальными. При вращении колес делительные конусы катятся друг по другу без скольжения.
Конические зубчатые передачи необходимо регулировать, добиваясь совпадения вершин делительных конусов колес.
Угол ∑ между осями зубчатых колес равен сумме углов делительных конусов ∑= δ1+ δ2 (рис. 16.1).
Достоинство конических передач - возможность передачи механической энергии между валами с пересекающимися осями.
Недостатками являются необходимость регулирования передачи (вершины делительных конусов должны совпадать), а также меньшая нагрузочная способность и большая сложность изготовления по сравнению с цилиндрическими передачами.
В конической передаче местом приложения силы Fmдейст-вующей перпендикулярно поверхности зуба, считают сечение на середине ширины зубчатого венца.
Для расчета валов и опор силу Fn удобно представить в виде со¬ставляющих: Fh F, и Ра.
Окружная
сила F,(H) на шестерне
где Т\ - вращающий момент, Н-м; dmi ~ средний делительный диа¬метр, мм.
В прямозубой передаче (рис. 16.5) для определения состав-ляющих запишем промежуточное выражение (aw = 20° - угол зацеп¬ления)
Радиальная сила на шестерне
осевая сила на шестерне
Силы на колесе соответственно равны
В передаче с круго¬вым зубом во избежание заклинивания зубьев при значительных зазорах в подшипникахнеобходи¬мо обеспечить направле¬ние осевой силы Fa\ на ведущей шестерне к ос¬нованию делительного конуса. Для этого на-правление вращения ве¬дущей шестерни (если смотреть со стороны вершины делитель¬ного конуса) и направление наклона зубьев должны совпадать. По рис. 16.7 шестерня вращается против хода часовой стрелки, т.е. влево, и зуб шестерни ле,-вый.
В передаче с круговым зубом при
соблюдении этого условия:
радиальная сила на шестерне
FA = F, (tgawcos 8, - sin (3„ sinS^/cos^ ,
осевая сила на шестерне
Fal =Ft(tgawsin8, +sinPwcos5,)/cospn,
Такие же знаки в формулах будут при вращении по ходу часовой стрелки ведущей шестерни с правым зубом
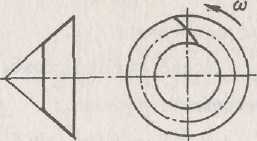
Силы на колесе соответственно равны: Fr2 = Fal; Fa2= Fri.
39-40
ПАРАМЕТРЫ ЧЕРВЯКА
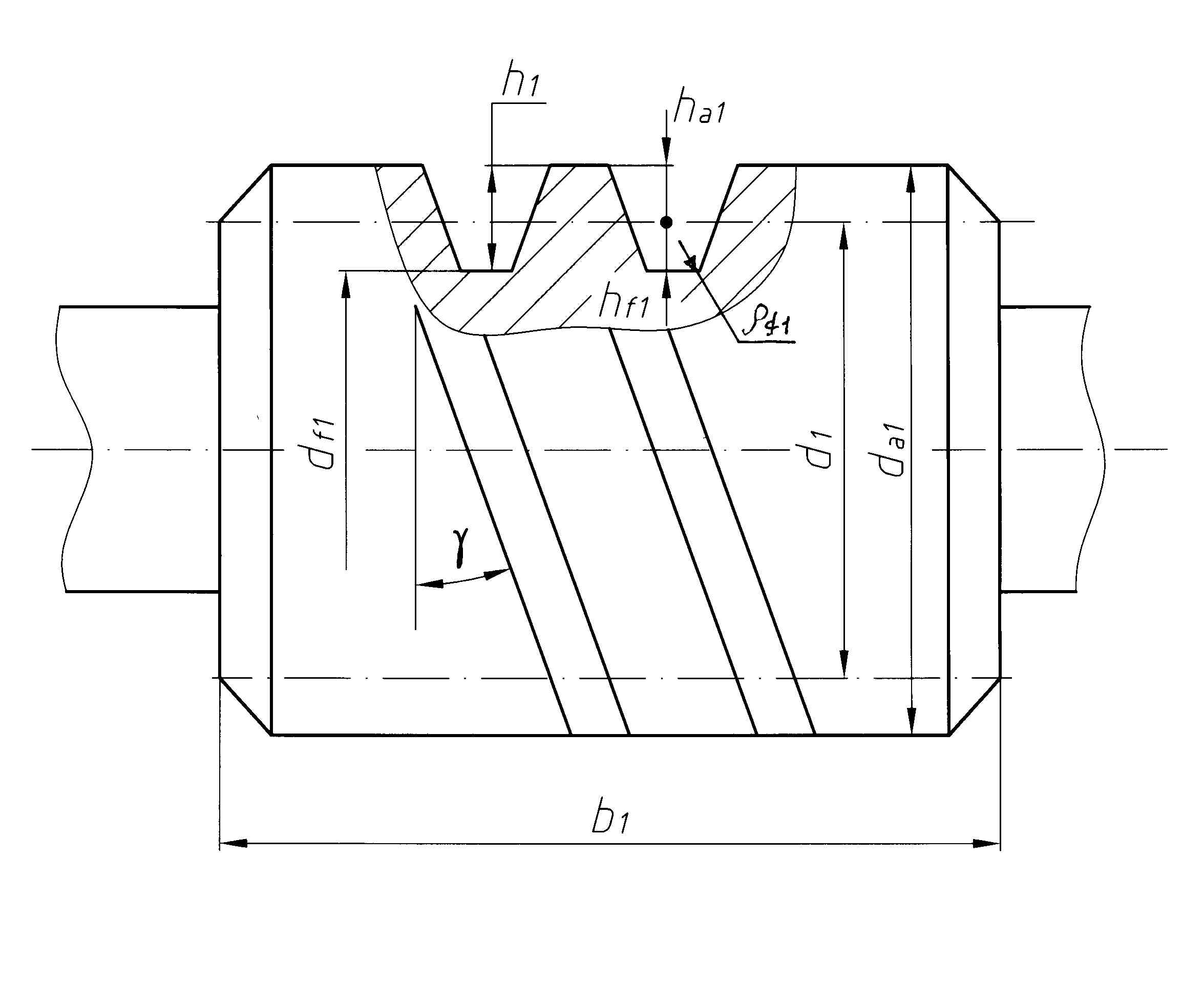Делительный
диаметр червяка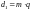
;
начальный
диаметр червяка
;
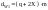делительный
угол подъёма витка
;
начальный угол
подъёма витка
;
для эвольвентного червяка определяют основной угол подъёма витка
;
и
основной диаметр червяка
;
высота
витка червяка
;
высота головки
витка червяка
;
диаметр
вершин витков червяка
;
радиус кривизны
переходной кривой червяка
.
В последних
формулах
– коэффициент высоты витка,
–
коэффициент высоты головки витка,
- коэффициент радиуса кривизны переходной
кривой.
При исходном
червяке по ГОСТ 19036-94
,
,
0,3,
для эвольвентных
червяков
.
Длина
нарезанной части червяка b
рассчитывается
как функция от числа зубьев колеса и
модуля m.
Выражение расчетной формулы зависит
от Z
(1, 2 и 4) и X
(-1, -0,5, 0, 0,5, 1).
X Расчётные формулы при Z
1 и 2 4
-1,0
-0,5
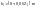
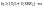
0
+0,5
+1,0
Примечания: 1. При промежуточном значении X длину b вычисляют по ближайшему значению X, которое даёт большее значение b .
2. Для шлифуемых и фрезеруемых червяков полученную по формулам длину b следует увеличить:
на 25 мм при
модуле
m<10
мм;
на 35- 40 мм при модуле m = 10 – 16 мм;
на 50 мм при модуле m>16 мм.