Системы координат. Декартова, полярная системы координат и их связь.
Системы координат
Любая точка на плоскости может быть однозначно определена при помощи различных координатных систем, выбор которых определяется различными факторами. Способ задания начальных условий для решения какой – либо конкретной технической задачи может определить выбор той или иной системы координат. Для удобства проведения вычислений часто предпочтительнее использовать системы координат, отличные от декартовой прямоугольной системы. Кроме того, наглядность представления окончательного ответа зачастую тоже сильно зависит от выбора системы координат. Ниже рассмотрим некоторые наиболее часто используемые системы координат.
Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрических уравнений.
Полярная система координат задаётся
лучом, который называют нулевым или
полярной осью. Точка, из которой выходит
этот луч, называется началом координат
или полюсом. Любая точка на плоскости
определяется двумя полярными координатами:
радиальной и угловой. Радиальная
координата (обычно обозначается
)
соответствует расстоянию от точки до
начала координат. Угловая координата,
также называется полярным углом или
азимутом
и обозначается
,
равна углу, на который нужно повернуть
против часовой стрелки полярную ось
для того, чтобы попасть в эту точку.[1]
Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.
Связанные термины: Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат (не прямоугольную)
Связь между декартовыми и полярными координатами
Пару полярных координат
и
можно
перевести в Декартовы
координаты
и
путём
применения тригонометрических функций
синуса
и косинуса:
в то время как две декартовы координаты и могут быть переведены в полярную координату :
(по
теореме
Пифагора).
Для определения угловой координаты следует принять во внимание два следующие соображения:
Для
,
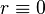может
быть произвольным действительным
числом.Для
,
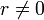чтобы получить уникальное значение
,
следует ограничиться интервалом в
.
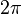Обычно выбирают интервал
или
.
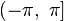Для вычисления
в
интервале
,
можно воспользоваться такими уравнениями
(
обозначает обратную функцию к тангенсу):
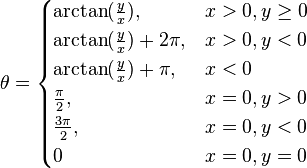
Для вычисления в интервале , можно воспользоваться такими уравнениями:[14]
Учитывая, что для вычисления полярного угла не достаточно знать отношение к , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты .