Алгоритм

Обозначения:

А - матрица, состоящая из n строк и k столбцов; A(i, j) - элемент матрицы, стоящий на i-ой строке, в j-ом столбце.

Алгоритм:

Основа алгоритма - цикл по всем элементам главной диагонали. Для квадратной матрицы размера n будет n итераций. Для прямоугольной матрицы, состоящей из n строк и k столбов, число итераций будет равно min(n, k). Пусть i - счетчик итераций.

Каждый проход цикла устроен следующим образом.

1. Если A(i, i) равен нулю, то в прямоугольнике (i, i, n, k) ищем ненулевой элемент. Если он не найден, то выходим из цикла. Если он найден, и его координаты (i2, j2), то меняем местами i-ую строку с i2-ой, и j-ый столбец с j2-ым. Делим i-ую строку матрицы на A(i, i). Таким образом A(i, i) теперь равен 1.

2. При помощи вычитания i-го столбца из всех столбцов стоящих правее, и i-ой строки из всех строк стоящих ниже, с определенными коэффициентами, зануляем все элементы вида А(i+1, i), A(i+2, i), ... A(n, i) и A(i, i+1), A(i, i+2), ... A(i, k).

3. Переходим к следующей итерации.

После цикла остается подсчитать сколько единиц стоит на главной диагонали. Их кол-во равно рангу. Если же их нет, то ранг равен 1.

9 Вопрос

Определитель матрицы А есть число, равное 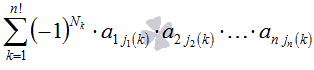 . Опишем эту формулу словами. Определителем квадратной матрицы порядка n на n является сумма, содержащая n! слагаемых. Каждое слагаемое представляет собой произведение n элементов матрицы, причем в каждом произведении содержится элемент из каждой строки и из каждого столбца матрицы А. Перед k-ымслагаемым появляется коэффициент ( -1 ), если элементы матрицы А в произведении упорядочены по номеру строки, а количество инверсий   в k-ой перестановке множества номеров столбцов нечетно. Определитель матрицы А обычно обозначается как  , также встречается обозначение det( A ). Также можно услышать, что определитель называют детерминантом. Итак,  .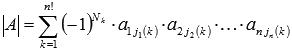

• Определитель не изменяется при транспонировании: det A^T = det A.

• При перестановке любых двух строк, определитель меняет знак.

• Если в определителе есть две одинаковые строки, то он равен нулю.

• Если все элементы строки определителя умножить на отличное от нуля число,

то определитель умножается на это число:

.

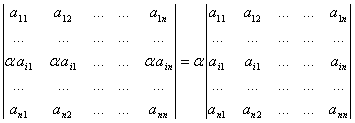• Определитель с двумя пропорциональными строками равен нулю.

• Определитель, содержащий нулевую строку, равен нулю.

• Если каждый элемент какой либо строки определителя представлен в виде суммы двух слагаемых:

то его можно представить в виде суммы двух определителей:

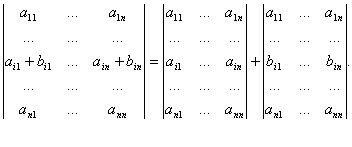
• Определитель не изменится, если к элементам любой его строки прибавить элементы

любой другой строки, умноженные на одно и то же число.

Поскольку определитель не меняется при транспонировании, приведенные выше утвкрждерия

справедливы и для столбцов.

10 Вопрос

Определение. Выражение

 называется определителем 2-го порядка.

Числа   – это элементы определителя. Определитель 2-го порядка имеет две строки и два столбца. Индексы, стоящие внизу соответствующего элемента, означают номер строки и номер столбца определителя, на пересечении которых стоит указанный элемент. Например, элемент   стоит в первой строке и втором столбце определителя.

Элементы  называют элементами главной диагонали определителя, а другие два элемента – соответственно элементами побочной диагонали.

Определение. Выражение

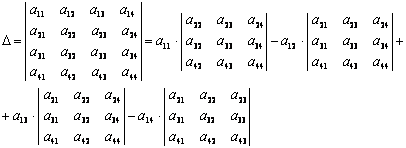
называется определителем 4-го порядка. Этот определитель можно записать в виде: ,      (1.6)

где  – это минор элемента, стоящего на пересечении i-ой строки, j-го столбца,   – его алгебраическое дополнение.