1 вопрос

Определение 1. Матрицей A называется любая прямоугольная таблица, составленная из чисел a_ij, которые называют элементами матрицы и обозначается

Определение 2. Если в выражении (1) m = n, то говорят о квадратной матрице, а если  , то о прямоугольной.

В зависимости от значений m и n различают некоторые специальные виды матриц:

1. Матрица - строка (или строковая матрица), состоящая из одной строки. Это прямоугольная матрица размером 1 x n.

A=(a₁₁ a₁₂ ... a_n).

2. Матрица - столбец ( столбцевая матрица), состоящая только из одного столбца. Это также прямоугольная матрица размером m x 1

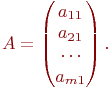
3. Матрица, состоящая из одного элемента. A=(a₁₁)_1x1=a₁₁.

4. Нулевая матрица, состоящая из одних нулей, в матричной алгебре играет роль 0, обозначается V.

5. Единичная матрица, состоящая из нулей, кроме главной диагонали, на которой стоят единицы. Обозначается E и играет роль единицы в матричной алгебре

6. Диагональная матрица, квадратная порядка n, состоящая из нулей и на главной диагонали стоят не равные нулю элементы (не обязательно единицы)

2 Вопрос

Сложение и вычитание матриц сводится к соответствующим операциям над их элементами. Самым главным свойством этих операций является то, что они определены только для матриц одинакового размера. Таким образом, возможно определить операции сложения и вычитания матриц:

Определение. Суммой (разностью) матриц является матрица, элементами которой являются соответственно сумма (разность) элементов исходных матриц.

c_ij = a_ij  b_ij

С = А + В = В + А.

Операция умножения матриц

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

AB = C;

            Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

 

Свойства операции умножения матриц.

 

1)Умножение матриц не коммутативно, т.е. АВ  ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называютсяперестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка.

АЕ = ЕА = А

            Очевидно, что для любых матриц выполняются следующее свойство:

AO = O;  OA = O,

где О – нулевая матрица.

 

            2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:

(АВ)С=А(ВС). 

            3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения  А(В+С) и (А+В)С, то соответственно:

А(В + С) = АВ + АС

(А + В)С = АС + ВС. 

            4) Если произведение АВ определено, то для любого числа  верно соотношение:

(AB) = (A)B = A(B). 

            5) Если определено произведение АВ , то определено произведение В^ТА^Т и выполняется равенство:

(АВ)^Т = В^ТА^Т, где

индексом Т обозначается транспонированная матрица.

3 Вопрос

  Элементарными преобразованиями матрицы называют следующие операции:

 перестановка любых двух строк матрицы;

 умножение любой строки на произвольное, отличное от нуля, число;

 сложение любой строки с другой строкой , умноженной на произвольное число;

 транспонирование матрицы.

Матрица A^T называется транспонированной по отношению к матрице A= {a_ij}, если A^T= {a_ji}:

 

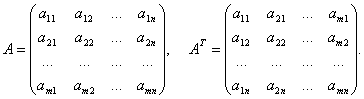
Иными словами, матрица, получающаяся из матрицы A  заменой строк столбцами, называется транспонированной по отношению к матрице A и обозначается A^T.

Элементарные преобразования не меняют ранга матрицы.

Эквивалентные матрицы

Определение. Матрицы, полученные в результате элементарного преобразования, называются эквивалентными.

            Надо отметить, что равные матрицы и эвивалентные матрицы - понятия совершенно различные.

Вопрос 4(не полностью)

Минор 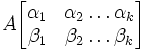  матрицы   ― определитель такой квадратной матрицы   порядка   (который называется также порядком этого минора), элементы которой стоят в матрице   на пересечении строк с номерами   и столбцов с номерами  .

Если номера отмеченных строк совпадают с номерами отмеченных столбцов, то минор называется главным, а если отмечены первые k строк и первые k столбцов ― угловым иливедущим главным.

Дополнительный минор элемента матрицы n-го порядка есть определитель порядка (n-1), соответствующий той матрице, которая получается из матрицы путем вычеркивания i-ой строки и j-го столбца.

Базисным минором матрицы называется любой её ненулевой минор максимального порядка. Для того чтобы минор был базисным, необходимо и достаточно, чтобы все окаймляющие его миноры (то есть содержащие его миноры на единицу большего порядка) были равны нулю. Система строк (столбцов) матрицы, связанных с базисным минором, является максимальной линейно независимой подсистемой системы всех строк (столбцов) матрицы.